XiaoMi-AI文件搜索系统
World File Search System义为
b'我们考虑由小型、自主设备组成的网络，这些设备通过无线通信相互通信。在为此类网络设计算法时，最小化能耗是一个重要的考虑因素，因为电池寿命是一种至关重要的有限资源。在发送和侦听消息都会消耗能量的模型中，我们考虑在任意未知拓扑的无线电网络中寻找节点最大匹配的问题。我们提出了一种分布式随机算法，该算法以高概率产生最大匹配。每个节点的最大能量成本为 O (log n )(log \xe2\x88\x86) ，时间复杂度为 O (\xe2\x88\x86log n )。这里 n 是节点数量的任意上限，\xe2\x88\x86是最大度数的任意上限； n 和 \xe2\x88\x86 是我们算法的参数，我们假设它们对所有处理器都是先验已知的。我们注意到，存在一些图族，对于这些图族，我们对能量成本和时间复杂度的界限同时达到多项对数因子的最优，因此任何显著的\xef\xac\x81 改进都需要对网络拓扑做出额外的假设。我们还考虑了相关问题，即为网络中的每个节点分配一个邻居，以便在最终节点发生故障时备份其数据。在这里，一个关键目标是最小化最大负载，定义为分配给单个节点的节点数。我们提出了一种有效的分散式低能耗算法，该算法确定一个邻居分配，其最大负载最多比最优值大一个多项对数 (n) 因子。'
b'我们考虑由小型、自主设备组成的网络，这些设备通过无线通信相互通信。在为此类网络设计算法时，最小化能耗是一个重要的考虑因素，因为电池寿命是一种至关重要的有限资源。在发送和侦听消息都会消耗能量的模型中，我们考虑在任意未知拓扑的无线电网络中寻找节点最大匹配的问题。我们提出了一种分布式随机算法，该算法以高概率产生最大匹配。每个节点的最大能量成本为 O (log n )(log \xe2\x88\x86) ，时间复杂度为 O (\xe2\x88\x86log n )。这里 n 是节点数量的任意上限，\xe2\x88\x86是最大度数的任意上限； n 和 \xe2\x88\x86 是我们算法的参数，我们假设它们对所有处理器都是先验已知的。我们注意到，存在一些图族，对于这些图族，我们对能量成本和时间复杂度的界限同时达到多项对数因子的最优，因此任何显著的\xef\xac\x81 改进都需要对网络拓扑做出额外的假设。我们还考虑了相关问题，即为网络中的每个节点分配一个邻居，以便在最终节点发生故障时备份其数据。在这里，一个关键目标是最小化最大负载，定义为分配给单个节点的节点数。我们提出了一种有效的分散式低能耗算法，该算法确定一个邻居分配，其最大负载最多比最优值大一个多项对数 (n) 因子。'
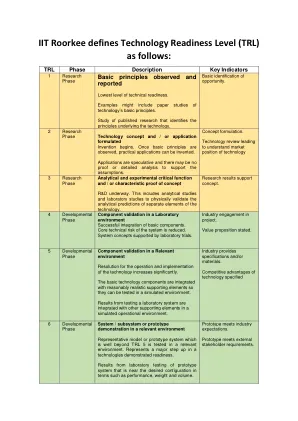
印度理工学院鲁尔基分校将技术就绪水平 (TRL) 定义为...
通过在模拟操作环境中的测试和演示对系统进行认证 技术已被证明可以在其最终形式和预期条件下工作。在几乎所有情况下，此 TRL 代表真正的系统开发的结束。 在预期运行的环境条件范围内对系统进行最终配置测试的结果。 评估它是否能满足其操作要求
![b“极值图论的一个核心问题是确定给定图 H 在 \xef\xac\x81x 大小的图中诱导副本的最大数量。这个问题最早由 Pippenger 和 Golumbic [13] 研究，近年来已成为广泛研究的主题 [2, 3, 7, 8, 11, 18]。本文重点关注有向图的类似问题。准确地说，设 H 是有向图。有向图 G 中 H 的诱导密度，表示为 i ( H, G )，是 G 中 H 的诱导副本数量除以 | V ( G ) | | V ( H ) | 。对于整数 n ，设 i ( H, n ) 为所有 n 顶点有向图 G 中 i ( H, G ) 的最大值。H 的诱导性定义为为 i ( H ) = lim n \xe2\x86\x92\xe2\x88\x9e i ( H, n )。当 i ( H, n ) 对于 n \xe2\x89\xa5 2 递减时，此极限存在。只有极少数有向图的可诱导性是已知的。一类重要的例子是有向星号。对于非负整数 k 和 \xe2\x84\x93 ，让有向星号 S k,\xe2\x84\x93 为通过对具有 k + \xe2\x84\x93 叶子的星号的边进行有向图，使得中心具有出度 k 和入度 \xe2\x84\x93 。有向星形是所有边都具有相同方向的定向星形，即星形 S k,\xe2\x84\x93 ，使得 k = 0 或 \xe2\x84\x93 = 0。S 2 , 0 和 S 3 , 0 的可诱导性由 Falgas-Ravry 和 Vaughan [5] 确定。为了解决 [5] 中的一个猜想，Huang [10] 扩展了他们的结果，确定了对所有 k \xe2\x89\xa5 2 的 S k, 0 的可诱导性，表明它是通过对入度为 0 的部分进行不平衡的弧爆破而渐近获得的。注意，由于任何有向图的可诱导性等于通过反转所有弧得到的有向图的可诱导性，因此可以考虑有向星号 S k,\xe2\x84\x93 ，使得 k \xe2\x89\xa5 \xe2\x84\x93 。特别地，Huang 的结果还确定了对所有 \xe2\x84\x93 的 S 0 ,\xe2\x84\x93 的可诱导性。 [10] 的结果未涵盖的最小定向星是 S 1 , 1 ，即三个顶点上的有向路径。Thomass\xc2\xb4e [16，猜想 6.32] 猜想 i ( S 1 , 1 ) = 2 / 5，这是通过四个顶点上的有向环的迭代爆炸获得的。](/simg/b/ba28460dd1b06d9996628290aa73355077ae7e14.webp)
b“极值图论的一个核心问题是确定给定图 H 在 \xef\xac\x81x 大小的图中诱导副本的最大数量。这个问题最早由 Pippenger 和 Golumbic [13] 研究，近年来已成为广泛研究的主题 [2, 3, 7, 8, 11, 18]。本文重点关注有向图的类似问题。准确地说，设 H 是有向图。有向图 G 中 H 的诱导密度，表示为 i ( H, G )，是 G 中 H 的诱导副本数量除以 | V ( G ) | | V ( H ) | 。对于整数 n ，设 i ( H, n ) 为所有 n 顶点有向图 G 中 i ( H, G ) 的最大值。H 的诱导性定义为为 i ( H ) = lim n \xe2\x86\x92\xe2\x88\x9e i ( H, n )。当 i ( H, n ) 对于 n \xe2\x89\xa5 2 递减时，此极限存在。只有极少数有向图的可诱导性是已知的。一类重要的例子是有向星号。对于非负整数 k 和 \xe2\x84\x93 ，让有向星号 S k,\xe2\x84\x93 为通过对具有 k + \xe2\x84\x93 叶子的星号的边进行有向图，使得中心具有出度 k 和入度 \xe2\x84\x93 。有向星形是所有边都具有相同方向的定向星形，即星形 S k,\xe2\x84\x93 ，使得 k = 0 或 \xe2\x84\x93 = 0。S 2 , 0 和 S 3 , 0 的可诱导性由 Falgas-Ravry 和 Vaughan [5] 确定。为了解决 [5] 中的一个猜想，Huang [10] 扩展了他们的结果，确定了对所有 k \xe2\x89\xa5 2 的 S k, 0 的可诱导性，表明它是通过对入度为 0 的部分进行不平衡的弧爆破而渐近获得的。注意，由于任何有向图的可诱导性等于通过反转所有弧得到的有向图的可诱导性，因此可以考虑有向星号 S k,\xe2\x84\x93 ，使得 k \xe2\x89\xa5 \xe2\x84\x93 。特别地，Huang 的结果还确定了对所有 \xe2\x84\x93 的 S 0 ,\xe2\x84\x93 的可诱导性。 [10] 的结果未涵盖的最小定向星是 S 1 , 1 ，即三个顶点上的有向路径。Thomass\xc2\xb4e [16，猜想 6.32] 猜想 i ( S 1 , 1 ) = 2 / 5，这是通过四个顶点上的有向环的迭代爆炸获得的。
b“极值图论的一个核心问题是确定给定图 H 在 \xef\xac\x81x 大小的图中诱导副本的最大数量。这个问题最早由 Pippenger 和 Golumbic [13] 研究，近年来已成为广泛研究的主题 [2, 3, 7, 8, 11, 18]。本文重点关注有向图的类似问题。准确地说，设 H 是有向图。有向图 G 中 H 的诱导密度，表示为 i ( H, G )，是 G 中 H 的诱导副本数量除以 | V ( G ) | | V ( H ) | 。对于整数 n ，设 i ( H, n ) 为所有 n 顶点有向图 G 中 i ( H, G ) 的最大值。H 的诱导性定义为为 i ( H ) = lim n \xe2\x86\x92\xe2\x88\x9e i ( H, n )。当 i ( H, n ) 对于 n \xe2\x89\xa5 2 递减时，此极限存在。只有极少数有向图的可诱导性是已知的。一类重要的例子是有向星号。对于非负整数 k 和 \xe2\x84\x93 ，让有向星号 S k,\xe2\x84\x93 为通过对具有 k + \xe2\x84\x93 叶子的星号的边进行有向图，使得中心具有出度 k 和入度 \xe2\x84\x93 。有向星形是所有边都具有相同方向的定向星形，即星形 S k,\xe2\x84\x93 ，使得 k = 0 或 \xe2\x84\x93 = 0。S 2 , 0 和 S 3 , 0 的可诱导性由 Falgas-Ravry 和 Vaughan [5] 确定。为了解决 [5] 中的一个猜想，Huang [10] 扩展了他们的结果，确定了对所有 k \xe2\x89\xa5 2 的 S k, 0 的可诱导性，表明它是通过对入度为 0 的部分进行不平衡的弧爆破而渐近获得的。注意，由于任何有向图的可诱导性等于通过反转所有弧得到的有向图的可诱导性，因此可以考虑有向星号 S k,\xe2\x84\x93 ，使得 k \xe2\x89\xa5 \xe2\x84\x93 。特别地，Huang 的结果还确定了对所有 \xe2\x84\x93 的 S 0 ,\xe2\x84\x93 的可诱导性。 [10] 的结果未涵盖的最小定向星是 S 1 , 1 ，即三个顶点上的有向路径。Thomass\xc2\xb4e [16，猜想 6.32] 猜想 i ( S 1 , 1 ) = 2 / 5，这是通过四个顶点上的有向环的迭代爆炸获得的。
将残疾重新定义为能力：解读视障人士的日常科技实践
摘要 全世界有超过十亿人患有某种形式的视力障碍，他们在日常生活中经常使用各种各样的技术。然而，人们对辅助和非辅助技术如何影响物质实践知之甚少。我们介绍了一项为期四个月的民族志研究的结果，该研究由英国一家支持视障人士的慈善机构的当地分支机构推动。我们的研究探讨了他们日常生活中的主流和辅助技术的使用。我们确定了技术使用的三个主要场所：社会关系和沟通实践、文本阅读实践和移动实践。通过民族志方法，我们有助于了解人们如何完成这些实践，并在此过程中发现使视障人士能够开展日常活动的实践能力。因此，我们研究如何从能力的角度来思考残疾，认为对能力的理解可以丰富适合视障人士需求的技术设计。
1.1 智能系统 AI 是计算机科学、心理学和哲学的结合。简而言之，我们可以将 AI 定义为使计算机智能地做事的研究 程序必须具备的能力 AI 程序必须具备的能力和智能特征，如学习、推理、接口以及接收和理解信息。对 AI 的理解 对相关术语的理解 智能、知识、推理、认知、学习和许多其他计算机相关术语。显示依赖于复杂问题，一般原则对这些问题没有多大帮助，尽管有一些有用的一般原则。对 AI 的第一种观点是，AI 是关于复制人脑所做的事情 第二种观点是，AI 是关于复制人脑应该做的事情 即合乎逻辑或理性地做事 ELIZA 这里简要提到了它的主要特征：智能模拟 响应质量 连贯性 语义 ELIZA 是一个用英语与用户对话的程序，就像 iPhone 中的 siri 一样。智能系统的分类为了设计智能系统，对这些系统进行分类非常重要 此类系统可能分为四种类别。
1.1 智能系统 AI 是计算机科学、心理学和哲学的结合。简而言之，我们可以将 AI 定义为使计算机智能地做事的研究 程序必须具备的能力 AI 程序必须具备的能力和智能特征，如学习、推理、接口以及接收和理解信息。对 AI 的理解 对相关术语的理解 智能、知识、推理、认知、学习和许多其他计算机相关术语。显示依赖于复杂问题，一般原则对这些问题没有多大帮助，尽管有一些有用的一般原则。对 AI 的第一种观点是，AI 是关于复制人脑所做的事情 第二种观点是，AI 是关于复制人脑应该做的事情 即合乎逻辑或理性地做事 ELIZA 这里简要提到了它的主要特征：智能模拟 响应质量 连贯性 语义 ELIZA 是一个用英语与用户对话的程序，就像 iPhone 中的 siri 一样。智能系统的分类为了设计智能系统，对这些系统进行分类非常重要 此类系统可能分为四种类别。
边界（重新）建构作为工作场所中人与非人类之间的内部作用 W. David Holford 魁北克大学蒙特利尔分校 本文提出了边界（重新）建构的概念。初始框架将主体通过制定现象塑造对象，正如对象反过来塑造主体的解释和经验一样。以下案例研究介绍强调了仍然存在于这个初始框架中的残余二元性。涉及混合类别和社会物质纠缠的本体论认识论洞察使我们能够随后将边界（重新）建构重新定义为人与物之间的内部作用（而不是相互作用）。有效的知识共享涉及富有成效的内部作用，而这反过来又需要内部作用成员之间的关系参与。这种参与需要管理层的努力，以确保工作场所内的心理安全网。引言 边界对象长期以来一直与实践社区联系在一起。原则上，这些对象是帮助在互动成员之间传递不同观点（即知识共享）的媒介。术语“边界”意味着这些对象位于两个或多个互动成员之间的社会交汇处。过去的研究经常探究边界对象的相对有效性，因此经常提出“关键”对象特征。对于管理者来说，这意味着关注
边界（重新）构建作为工作场所中人类与非人类之间的内部行动 W. David Holford 魁北克大学蒙特利尔分校 本文提出了边界（重新）构建的概念。初始框架描述了主体通过制定现象塑造客体，正如客体塑造主体的解释和经验一样。以下案例研究介绍重点介绍了仍然存在于初始框架中的残余二元性。涉及混合类别和社会物质纠缠的本体论认识论见解使我们能够随后将边界（重新）构建重新定义为人与物之间的内部行动（而不是相互作用）。有效的知识共享涉及富有成效的内部行动，而这反过来又需要内部行动成员之间的关系参与。这种参与需要管理层的参与，以确保工作场所内的心理安全网。简介 边界对象长期以来一直与实践社区相关联。原则上，这些对象是帮助在交互成员之间传递不同观点（即知识共享）的媒介。“边界”一词意味着此类对象位于两个或多个交互成员之间的社会交汇处。过去的研究经常探究边界对象的相对有效性，因此经常提出“关键”对象特征。对于管理者-实践者来说，这意味着关注有形的技术/物理属性。另一方面，本文主张将重点转向更多无形的人为/主观因素。随着这种重视程度的提高，管理层和成员在各自的行为和态度方面的责任也随之增加。为此，我们对边界对象的基本假设（即本体论或存在理论的问题）以及我们如何理解它们（即认识论或知识理论的问题）将受到质疑。在下文中，我们首先回顾了边界对象文献中过去的认识论和本体论立场，以及这些立场有时如何误导我们识别“有效边界对象”条件的重复处方，而这些处方未能充分强调人与物体的相互作用动态。接下来是替代性的认知、认识论和本体论线索，这些线索使我们能够将分析水平转向首先问自己哪些关键的有利条件允许获得有效的知识
![第 9 章 巴甫洛夫、斯金纳和其他行为主义者对人工智能的贡献 *** Witold Kosinski 和 Dominika Zaczek-Chrzanowska 波兰-日本信息技术研究所，波兰-日本计算机技术研究中心 ul. Koszykowa 86, 02-008 Warszawa wkos@pjwstk.edu.pl mado@pjwstk.edu.pl 摘要 将在真实和人工系统的背景下提供一种智能行为的定义。将简要介绍学习原理，从巴甫洛夫的经典条件作用开始，到桑代克和斯金纳的强化反应和操作性条件作用，最后到托尔曼和班杜拉的认知学习。本文将描述行为主义中最重要的人物，尤其是那些对人工智能做出贡献的人物。本文将介绍一些根据这些原理行事的人工智能工具。本文将尝试说明何时一些简单的行为修改规则可以导致复杂的智能行为。 1. 智能：描述 毫无疑问，行为主义者对人工智能的发展做出了巨大贡献。动物学习理论的证据，尤其是行为主义者发现的学习规律，多年来吸引了人工智能领域的研究人员，许多模型都以此为基础。智能是一个复杂而有争议的概念，因此很难用一个简单的定义来概括它。根据 Jordan 和 Jordan [1] 的说法，将智能视为我们用来描述具有一定质量的行为的概念是恰当的。在这方面应该使用两个标准，即速度（即代理执行需要智力的特定任务的速度）和能力（即代理可以执行的任务的难度）。另一方面，我们可以找到另一种智能定义，即执行认知过程的能力。有三个基本的认知过程：1) 抽象，2) 学习，3) 处理新颖性。该领域的杰出研究人员对智力给出了许多定义，例如，它被定义为：](/simg/6/627f48c0041fd2d34b503b6ed02bb4f19b9f3644.png)
第 9 章 巴甫洛夫、斯金纳和其他行为主义者对人工智能的贡献 *** Witold Kosinski 和 Dominika Zaczek-Chrzanowska 波兰-日本信息技术研究所，波兰-日本计算机技术研究中心 ul. Koszykowa 86, 02-008 Warszawa wkos@pjwstk.edu.pl mado@pjwstk.edu.pl 摘要 将在真实和人工系统的背景下提供一种智能行为的定义。将简要介绍学习原理，从巴甫洛夫的经典条件作用开始，到桑代克和斯金纳的强化反应和操作性条件作用，最后到托尔曼和班杜拉的认知学习。本文将描述行为主义中最重要的人物，尤其是那些对人工智能做出贡献的人物。本文将介绍一些根据这些原理行事的人工智能工具。本文将尝试说明何时一些简单的行为修改规则可以导致复杂的智能行为。 1. 智能：描述 毫无疑问，行为主义者对人工智能的发展做出了巨大贡献。动物学习理论的证据，尤其是行为主义者发现的学习规律，多年来吸引了人工智能领域的研究人员，许多模型都以此为基础。智能是一个复杂而有争议的概念，因此很难用一个简单的定义来概括它。根据 Jordan 和 Jordan [1] 的说法，将智能视为我们用来描述具有一定质量的行为的概念是恰当的。在这方面应该使用两个标准，即速度（即代理执行需要智力的特定任务的速度）和能力（即代理可以执行的任务的难度）。另一方面，我们可以找到另一种智能定义，即执行认知过程的能力。有三个基本的认知过程：1) 抽象，2) 学习，3) 处理新颖性。该领域的杰出研究人员对智力给出了许多定义，例如，它被定义为：
第 9 章 巴甫洛夫、斯金纳和其他行为主义者对人工智能的贡献 *** Witold Kosinski 和 Dominika Zaczek-Chrzanowska 波兰-日本信息技术研究所，波兰-日本计算机技术研究中心 ul. Koszykowa 86, 02-008 Warszawa wkos@pjwstk.edu.pl mado@pjwstk.edu.pl 摘要 将在真实和人工系统的背景下提供一种智能行为的定义。将简要介绍学习原理，从巴甫洛夫的经典条件作用开始，到桑代克和斯金纳的强化反应和操作性条件作用，最后到托尔曼和班杜拉的认知学习。本文将描述行为主义中最重要的人物，尤其是那些对人工智能做出贡献的人物。本文将介绍一些根据这些原理行事的人工智能工具。本文将尝试说明何时一些简单的行为修改规则可以导致复杂的智能行为。 1. 智能：描述 毫无疑问，行为主义者对人工智能的发展做出了巨大贡献。动物学习理论的证据，尤其是行为主义者发现的学习规律，多年来吸引了人工智能领域的研究人员，许多模型都以此为基础。智能是一个复杂而有争议的概念，因此很难用一个简单的定义来概括它。根据 Jordan 和 Jordan [1] 的说法，将智能视为我们用来描述具有一定质量的行为的概念是恰当的。在这方面应该使用两个标准，即速度（即代理执行需要智力的特定任务的速度）和能力（即代理可以执行的任务的难度）。另一方面，我们可以找到另一种智能定义，即执行认知过程的能力。有三个基本的认知过程：1) 抽象，2) 学习，3) 处理新颖性。该领域的杰出研究人员对智力给出了许多定义，例如，它被定义为：