XiaoMi-AI文件搜索系统
World File Search System二项式
![机器学习[R17A0534]讲义](/simg/g:\will\search\icon\source\b\b04497115176d4bfc8e822e2e357b3b536e9ea6c.webp)
机器学习[R17A0534]讲义
单元I：机器学习介绍，学习模型，几何模型，概率模型，逻辑模型，分组和分级，设计学习系统，学习类型，学习，监督，无监督，增强，观点和问题，版本空间，PAC学习，PAC学习，VC尺寸。单元II：有监督和无监督的学习决策树：ID3，分类和回归树，回归：线性回归，多线性回归，逻辑回归，神经网络：简介，感知，多层感知，支持向量机：线性和非线性，线性和非线性，内核功能，K最近的邻居。聚类简介，K-均值聚类，K-Mode聚类。单元III：合奏和概率学习模型组合方案，投票，错误纠正输出代码，包装：随机林木，增强：Adaboost：堆叠，堆叠。高斯混合模型 - 期望 - 最大化（EM）算法，信息标准，最近的邻居方法 - 最近的邻居平滑，有效的距离计算：KD -Tree，距离测量。第四单元：加强学习和评估假设的介绍，学习任务，Q学习，非确定性奖励和行动，时间差异学习，与动态编程的关系，主动的加强学习，在增强学习中的概括。动机，抽样理论的基础：误差估计和估计二项式比例，二项式分布，估计器，偏见和差异单位V：遗传算法：动机，遗传算法：代表假设，遗传操作员，遗传操作员，适应性和选择，示例性的探索，遗传探索，遗传学探索，遗传学的探索，模型：效果，并行化遗传算法。
公共卫生phc 6945
1。统计概率和采样分布的主要关键概念，例如标准正常，t，f，二项式，泊松，多项式和卡方。2。将常见的统计方法用于推理，包括估计，置信区间以及单变量或多元假设检验。3。应用和解释各种多变量回归方法，例如线性，逻辑和生存模型。4。开发用于使用统计软件（例如SAS/R）的实用技能，用于公共卫生研究的数据管理，集成，分析和解释。5。与给定的研究问题一起开发了与公共卫生问题有关的统计数据分析的书面和口头介绍，以及通过使用较少的技术术语将这些问题传达给从业人员的能力。
接受骨髓纤维化治疗的患者
二项式反应/无反应终点可能无法完全表征骨髓纤维化治疗的贫血相关益处。在这些对来自第 2 和第 3 阶段试验的骨髓纤维化患者随时间输血负担的新分析中，momelotinib 与未使用和使用过 JAK 抑制剂的人群的平均红细胞输血负担减少有关。在所有试验中，≥ 77% 接受 momelotinib 治疗的患者与基线相比保持或经历了输血强度的改善，这突出表明 momelotinib 为大多数骨髓纤维化患者提供了持续的贫血益处。目的：贫血是骨髓纤维化的主要特征，通常通过红细胞 (RBC) 输血进行治疗，这可能导致负面预后、生活质量和医疗保健相关的经济影响。 Janus 激酶 (JAK) 1/JAK2/激活素 A 受体 1 型抑制剂 momelotinib 获批用于治疗骨髓纤维化和贫血患者，其依据是临床试验中贫血、脾脏和症状获益的证据，这些获益以二项式反应/无反应终点表示。在本事后描述性分析中，进一步描述了 momelotinib 对未使用和使用过 JAK 抑制剂的患者中 RBC 输血负担随时间的影响。方法：在基线和 24 周治疗期间收集所有输血的 RBC 单位，最初在单组 2 期研究中作为概念验证分析，然后在 3 期 SIMPLIFY-1、SIMPLIFY-2 和 MOMENTUM 研究中分别与对照药物（芦可替尼、最佳可用疗法 [BAT] 和达那唑）进行比较。结果：在第 2 阶段研究中，平均输血需求变化为 -1.5 单位/28 天，85% 的患者 (35/41) 实现了输血量数字减少。在 SIMPLIFY-1、SIMPLIFY-2 和 MOMENTUM 中，平均输血需求下降
泰米尔纳德邦政府公报
单元I数学物理学维度分析：微分方程（普通和部分） - 方程顺序 - 梯度，发散，卷曲和laplacian的表达式 - 矢量代数和矢量计算 - 高斯分歧定理 - 格林的定理 - Stokes的定理。矩阵：Cayley - 汉密尔顿定理，矩阵倒数 - 特征值和特征向量。多项式：Hermite，Bessel和Legendre功能。特殊功能：beta和伽马功能。概率：基本概率理论 - 随机变量 - 二项式 - 泊松和正态分布。复杂变量：分析函数 - 奇异点 - 库奇的积分定理和公式-Taylor's和Laurent的扩展，杆子，残基的计算以及积分的评估。积分变换：傅立叶系列和傅立叶变换及其属性。
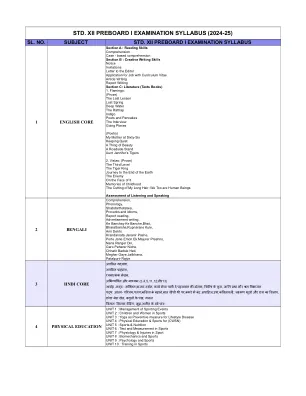
std。 XII预板I考试教学大纲（2024-25）
1。矩阵和决定因素2。“应用矩阵和决定因素（使用矩阵方法和Cramer的规则同时解决系统的求解系统）” 3。“高阶衍生物4。应用导数（切线和正常方程，增加和减少功能，使用衍生物找到最大值和最小值，边际成本和边际收入）” 5。LPP 6模型算术和一致性模型7。概率分布（数学期望，差异，二项式分布，泊松分布，正态分布）8。Alligation＆Rigation，Boats＆Streams，Pipes＆Pisters＆Scisterns，Races＆Games，Races＆Games，数字不平等9.时间序列10。推论统计（人口和样本，参数和统计，t检验一个样本，两个独立样本）11。金融数学12。积分（不确定和确定）13。应用积分（曲线下的区域，消费者和生产者盈余）
行为流行病学：评估的经济模型......
6 我们考虑到了医院以及食品和天然气供应链等基本服务的必要性，¯ 𝜆 代表该阈值。7 这三个参数（𝑐，𝜙 +，𝜙 −）背后的想法是，在一个层面上，我们希望将不参加社交活动的机会成本与实际感染的成本区分开来，在另一个层面上，我们希望将被感染的一次性成本分解为感染他人的个人成本和利他主义关切。8 另一个主要候选者是泊松或几何到达，它是平稳的，因此可以确保疫苗在大流行开始两个月后到达的可能性与在 12 个月时 14 个月内开发出来的可能性相同。该分布是负二项式的极限情况，其中均值和方差重合。例如，Alvarez 等人 [2021] 和 Farboodi 等人 [20] 就使用过这种方法。 [ 2021 ]。
基于自动化的定量检查方法
10确定可能的数字或数字组合的频率用于数字分析，因此必须区分前面的数字（第一，第二，第三方数字等），对于金钱而言，要考虑来自后面的数字（一个欧洲职位，十欧元的职位等）。实证研究，经济数据中的“首次项目”和“第二个零”具有频率分布，这显着偏离随机相等分布，并且可以在统一功能（“ Benford Law”或“ Newcomb-Benford-law”）中进行描述。通过检查评估的数字分布，可以发现单个数字是否过于罕见或过于频率，这可以表明使用单个数字时的无意识的偏好或不喜欢纳税人对数据的操纵。可以在概率测试“ Chi-Quadrat调整测试”（整个拨号分布）或“二项式分布”（单个数字）的帮助下评估观察到的频率分布的一致性和预期频率分布。