XiaoMi-AI文件搜索系统
World File Search System8-9P 吉井勇 4.ai
1934 年至 1937 年间,Isamu 在伊诺诺隐居。 Isamu之所以选择这里,是因为他喜欢伊诺诺市的自然风光和当地的人民,伊诺诺市的人民也喜欢Isamu并欢迎他。 即使在 Isamu 回国后,Inono 的人们仍然无法忘记他,并开始努力为他的诗立一座纪念碑。 1994年,当地居民在井野地区竖立了13座纪念碑,在长濑地区竖立了2座纪念碑。纪念碑的石头是由根须的小松石工所捐赠的。诗句是从勇在伊诺诺时创作的约2300首诗中选出的,由伊诺诺的各个小组选定,并在小组长会议上确定。如果参观完这些古迹,就可以一次性游遍伊诺诺市。 希望大家能够借此机会参观刻有吉井勇诗歌的纪念碑,并通过他的诗歌了解井野市的自然美景、山区生活以及当地人民的热情好客。
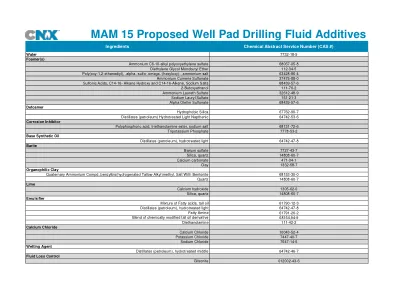
MAM 15提出的井垫钻孔液添加剂MAM 15提出的井垫钻孔液添加剂
水7732-18-5泡沫(S)C6-10-烷基聚氧硫酸盐硫酸盐68037-05-8二乙二醇单丁基单丁基112-34-5聚(Oxy-1,2-乙基) 63428-86-4碳硫酸铵37475-88-0磺酸,C14-16-烷烃羟基和C14-16-烷烯,钠盐68439-57-6 151-21-3α烯丙基磺酸盐68439-57-6 DEDOAMER疏水二氧化硅67762-90-7蒸馏(石油)氢化光核糖64742-53-53-53-5磷酸盐7778-53-2碱基合成油馏出(石油),氢化光64742-47-8硫酸盐硫酸盐7727-43-7硅,石英14808-60-7
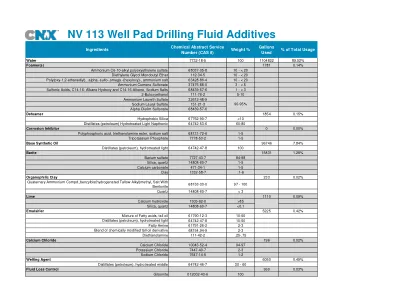
NV 113井垫钻孔液添加剂
Water 7732-18-5 100 1104822 89.52% Foamer(s) 1781 0.14% Ammonium C6-10-alkyl polyoxyethylene sulfate 68037-05-8 10 - < 20 Diethylene Glycol Monobutyl Ether 112-34-5 10 - < 20 Poly(oxy-1,2-ethanediyl), 。 2-二氧乙醇111-76-2 5-10硫酸铵32612-48-99午睡64742-53-6 60-80腐蚀抑制剂0 0.00%多磷酸,三氨基酯酯,钠盐68131-72-6 1-5磷酸三)磷酸盐7778-53-2 1-5 1-5碱基合成油96746 7.845%; 64742-47-8 100 Barite 1.28%硫酸钡7727-43-7 84-98硅,石英14808-60-7 1-5碳酸钙471-34-1 1-5 Compd。,苄基苯基(氢化牛脂烷基)甲基,盐盐68153-30-0 97-100
AI x 设计井上光和
1) https://aws.amazon.com/jp/ 2) https://cloud.google.com/products/ai/ 3) https://www.ibm.com/watson/ 4) https://azure.microsoft.com/ja-jp/services/cognitive-services/ 5) https://trends.google.co.jp/trends/ 6) https://colab.research.google.com/ 7) http://jupyter.org/ 8) https://www.anaconda.com/ 9) http://archive.ics.uci.edu/ml/datasets/Iris 10) http://lib.stat.cmu.edu/datasets/boston 11) https://archive.ics.uci.edu/ml/datasets/wine+quality 12) http://yann.lecun.com/exdb/mnist/ 12) http://megaface.cs.washington.edu/ 14)ReLU(Ramp函数):激活函数之一。当输入值为0以下时,变为0,当大于1时,则按输入原样输出。 15)Softmax函数:将判断结果以百分比的形式输出到输出层的各个单元。一般取百分比最高者作为答案。 16)铃木隆宏,《工作的消失》,讲谈社,2017,第76页 17)新井纪子,《人工智能与不会读教科书的孩子》,东洋经济,2018年 18)小川宏,《中小学编程教育及其在地区的实践》,日本艺术设计协会期刊第77期,2018年,第50-51页 19)迈克尔·施密特、Hod Lipson,《从实验数据中提炼自由形式的自然法则》,2009年,《科学》第324卷 计算机从摆动的钟摆的运动中推导出运动定律。 20)大脑中的侏儒:脑外科医生彭菲尔德绘制的图表,显示了人类大脑皮层的运动区和体感区与身体各部位之间的对应关系。
Tomoki Fujii(Fujii Tomoki),2025年1月...
35。T. Fujii和D. Roland-Holst(2008)“越南对世界贸易组织的加入如何改变贫困的空间发病率?”在全球化和亚洲的穷人中:共享的增长可以维持吗?,由M. Nissanke和E. Thorbecke编辑。pp。47-89。Palgrave Macmillan。[工作文件版本:世界银行政策研究工作文件4521]
单纯井
Sumplex Wellness从事业务已有30多年的历史,开创了员工健康和健康在工作场所的作用。他们为雇主群体提供了全面的服务,以增强人们的健康和福祉。Sumplex Wellness以其动手,积极主动的方法来满足客户需求而感到自豪。通过虚拟能力在费城和周围地区和周围地区为客户提供服务。Primary contact Lauren Shelly ibcwellness@simplexwellness.com Website www.simplexwellness.com Areas of Focus: Select to view available programs Be Active Be Nourished Be Energized Be Empowered Biometric Screenings Challenges Wellness Fairs/Days Turnkey and Value-Added Services
1香农安全和一次性垫
我们如何知道这是计算安全的?我们没有。如果人们假设模块化指数是单向函数,则计算有限的窃听器EVE只有可忽略的概率可以恢复Alice's或Bob的Secret Key,A或B。在不知道{a,b}之一的情况下,对于G a和g b(mod q)的值而言,对于计算G AB(mod Q)的算法很难计算GAB(mod Q)。但是,这并不意味着我们知道如何从离散对数很难计算的假设中证明Di-e-Hellman密钥交换协议的安全性。相反,基于二型 - 赫尔曼密钥交换的安全性的假设称为决策局限性局部假设(DDH)假设。它涉及区分形式(g a,g b,g ab)(mod q)的有序三元组的问题,即形式的有序三元组(g a,g b,g c)(mod q)(mod q),当q是一个较大的素数并且G Modulo Q的顺序是另一个大的prime p。如果a,b,c从[p]随机随机取样,则DDH的假设是对于任何有效的可计算测试τ,概率prτ(g a,g b,g ab)= 1和prτ(g a,g b,g b,g b,g c)= 1 = 1 di e tif.1(n = n = log),以及n = 2(p),以及二(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(p)(P) n的逆多项式函数。换句话说,DDH假设基本上只是一种说明Di-Hellman密钥交换在计算上是安全的一种方式。