XiaoMi-AI文件搜索系统
World File Search System方案-教学大纲-B.E.-机械工程.pdf
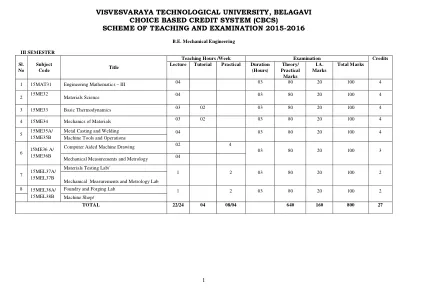
课程名称:工程数学 - III 课程代码:15MAT31 学分:04 L-T-P:4-0-0 每周接触时间:04 总时间:50 考试。分数:80 IA 分数:20 考试。小时数:03 课程目标:本课程的目标是通过让学生学习傅里叶级数、傅里叶变换和 Z 变换、统计方法、数值方法求解代数和超越方程、矢量积分和变分法,向学生介绍不同工程领域中最常用的分析和数值方法。模块 RBT 级别
EE-电气与计算机工程
EE 743. 工程中的数值方法。3 小时。本课程涵盖了广泛工程应用和数据分析的数值方法理论和实践。主题包括数值微积分、线性代数和优化。学生将接触到卷积神经网络、压缩感知、特征脸、稳定性、主成分分析、k 均值聚类、使用活动轮廓进行图像分割、噪声中信号检测和函数拟合等现代主题。本课程提供编程数值分析算法的实践经验。
从第一原理学习理论
1个数学初步3 1.1线性代数和不同的演算。。。。。。。。。。。。。。。。。3 1.1.1最小化二次形式。。。。。。。。。。。。。。。。。。。3 1.1.2反转2×2矩阵。。。。。。。。。。。。。。。。。。。。。。。。4 1.1.3反相矩阵由块,矩阵反转引理定义。。4 1.1.4特征值和奇异值分解。。。。。。。。。。。。6 1.1.5差分线。。。。。。。。。。。。。。。。。。。。。。。。。。7 1.2浓度不平等。。。。。。。。。。。。。。。。。。。。。。。。。。。7 1.2.1 Hoe ting的不平等。。。。。。。。。。。。。。。。。。。。。。。。。10 1.2.2 McDiarmid的不平等。。。。。。。。。。。。。。。。。。。。。。。。13 1.2.3伯恩斯坦的不平等(♦)。。。。。。。。。。。。。。。。。。。。。。14 1.2.4期望最大值。。。。。。。。。。。。。。。。。。。。。16 1.2.5通过正交(♦♦)对期望的估计。。。。。。。18 1.2.6随机矩阵(♦♦)的浓度不平等。。。。。。。19
Adrian She – - 计算机科学系
- 量子 BC 研究日,2023 年 4 月(海报展示)。 - 量子信息与计算机科学联合中心 (QuiCS) 研讨会,2023 年 5 月。 - SIAM 应用代数几何会议,“量子信息中的代数和几何结构”小型研讨会,2023 年 7 月。 - UBC 理论计算机科学研讨会,2023 年 10 月。 - 滑铁卢大学 IQC CS/数学研讨会,2023 年 11 月。 - 多伦多大学理论研讨会,2024 年 5 月。
MATH1020-微积分和线性代数II-单位指南
单元描述Math1010中引入的线性代数和微积分的基础进一步探索和扩展。用代数涵盖的主题包括:反矩阵,决定因素,矢量空间和子空间,特征值以及特征向量以及线性变换。在微积分中,主题包括:限制,连续性和衍生物,数值集成,多项式,序列和序列和微分方程的进一步发展。另外,引入了两个或多个变量的复数和计算。学生在整个课程中都利用数学软件来支持和加强解决各种理论和实际问题的问题。
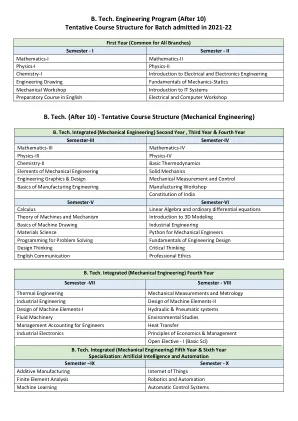
BTI 课程结构 2021-22 (1).pdf
第三学期 第四学期 数学-III 数学-IV 物理-III 物理-IV 化学-II 基础热力学 机械工程要素 固体力学 工程制图与设计 机械测量与控制 制造工程基础 制造业研讨会 印度宪法 第五学期 第六学期 微积分 线性代数和常微分方程 机器与机构理论 3D 建模简介 机械制图基础 工业工程 材料科学 机械工程师的 Python 编程 问题解决 工程设计基础 设计思维 批判性思维 英语交流 职业道德
课程vitae mehmet可以-Lelystad
•向Havo和VWO学生提供辅导数学,物理,化学。•在电气工程,控制技术,数字信号处理,微积分,线性代数和HBO和WO学生的差分比较中进行辅导。•监督时间表。•在职业选择中提供建议。•从HBO到TU的领导学生。•给教学课程涉及智能和高效学习。•从商业界监督人员。网站:http://www.canbijles.nl毕业工作和实习期:2009年3月至2010年2月的职能:研究生硕士组织:Nikhef(阿姆斯特丹国家亚原子化学研究所)。职责: