XiaoMi-AI文件搜索系统
World File Search SystemCS234:加固学习 - 问题会话#1
假设我们有一个无限 - 摩托克,折扣的MDP M =⟨S,A,R,T,γ⟩具有有限的状态行动空间,| S×A | <∞和0≤γ<1。对于任何两个任意集x和y,我们将所有函数的类表示从x到y的所有函数的类别为{x→y}≜{f | F:X→Y}。在随后的问题中,令q,q'∈{s×a→r}是任意两个任意的动作值函数,并考虑任何固定的状态s∈S。没有一般性丧失,您可以假设Q(s,a)≥Q'(s,a),∀(s,a)∈S×a。
量子力学:保持真实吗?
众所周知,埃尔温·薛定谔在发现量子理论时,曾想将量子波函数ψ解释为表示电荷在三维空间中传播的连续分布。但人们不太了解的是,薛定谔最初也希望他的波函数用实值函数而不是复值函数来表示。在关于量子理论的一些早期论文以及写给亨德里克·洛伦兹和马克斯·普朗克的信中,薛定谔描述了他寻找实值波动方程的进展和挣扎,尽管他知道以他的名字命名的复值方程。最终,他发现了一个完全实的方程,等同于薛定谔方程,并将其称为“标量场ψ的均匀和一般波动方程”(2020,163)。在普朗克看来,他把这一突破描述为“闻所未闻的简单和闻所未闻的美”(Przibram 1967,16)。本文是探索这种形式的薛定谔方程的一种广告。假设我们将这个实方程视为量子理论的另一种表述,比如海森堡表述,甚至视为提供一种不同的本体论,将波函数的实部与 JS Bell 2004 所称的可视对象联系起来。我们是否会以不同的方式看待一些未解决的问题,又会出现什么新问题?在概述历史和一些背景之后,我将说明如何使用这种替代形式来理解量子基础中的问题。受 Struyve 2020 的最新论文的启发,我将展示“实薛定谔方程”如何极大地改变量子理论中关于时间反转不变性的难题。我希望读者能找到其他类似的例子,其中“保持真实”可以有所帮助。
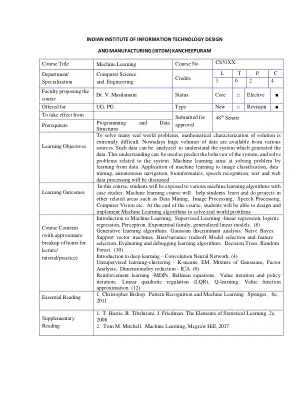
机器学习(4个学分)
机器学习介绍,监督学习 - 线性回归,逻辑回归,感知。指数族,广义线性模型。(8)生成学习算法。高斯判别分析。幼稚的贝叶斯。支持向量机。偏见/方差权衡模型选择和特征选择。评估和调试学习算法,决策树,随机森林。(10)深度学习简介 - 卷积神经网络。(4)无监督的学习聚类 - k-均值,em,高斯的混合物,因子分析。降低降低 - ICA。(8)增强学习-MDP,Bellman方程,价值迭代和政策迭代,线性二次调节(LQR),Q学习。值函数近似。(12)
基于事件的联合Q学习
我们介绍了基于事件的QAVG(EBQAVG)算法,该算法将基于事件的通信集成到联合Q学习中。QAVG由(Jin等人,2022),在局部计算和全局聚集之间交替。每个代理都会在服务器汇总所有N代理的值函数之前执行其值函数的多个本地更新。为了提高沟通效率,连续的聚集之间执行了几个本地更新。遵循相同的本地更新和聚合结构,基于事件的QAVG算法使代理只有在发生重大更改时才可以将Q-table更新传达给中央服务器,从而减少了不必要的通信开销。我们提供了算法及其通信协议的详细描述。
基于Bellman的强化学习中的理论障碍
对此限制的潜在补救措施正在扩大算法利用的反馈。一种这样的方法是事后观察经验重播(她)(Andrychowicz等,2017)。她建立在Bellman方程式上以学习通用价值功能(Sutton等,2011; Schaul等,2015)。假设目标是达到某种目标状态,标准值函数仅根据其达到此目标的能力来估计状态的价值。相比之下,通用价值函数可预测任何其他状态的任何状态。她利用学习过程中遇到的状态来学习这种普遍的价值功能,利用富裕的反馈,而不是达到目标是否达到目标。考虑到这一点,文献中的几项作品应用于ATP(Aygéun等,2022; Trinh等,2024; Poesia等,2024)。
B.Sci. (数据科学与人工智能)课程适用于 2018 年或以后入学的学生
MH1802 科学微积分 本课程旨在让学生掌握 数学知识和分析技能,使他们能够应用微积分技术(以及他们现有的数学技能)来解决适用的科学问题; 数学阅读技能,使他们能够阅读和理解基础和流行科学和工程文献中的相关数学内容;以及 数学交流技能,使他们能够有效和严格地向数学家、科学家和工程师介绍他们的数学思想。内容基础 (BAS) 数字类型;函数和图形;常用函数及其图形;重要的代数、三角、对数和指数恒等式;基本复数。微积分 (DIF) 极限;微分;微分技术;微分的应用;基本偏导数。积分 (INT) 积分;积分技术;对数、指数和反三角函数的微积分;积分的应用;微分方程 (DE) 基础;一阶常微分方程;二阶常微分方程;级数、序列和微分方程。MH1812 离散数学 学习目标 本课程介绍数学和计算机科学中常用的离散数学基本概念。内容 - 计数、排列和组合、二项式定理 - 递归关系 - 图、路径和电路、同构 - 树、生成树 - 图算法(例如最短路径、最大流)及其计算复杂度、大 O 符号 MH2100 微积分 III 学习目标 这是微积分系列中的最后一门课程。本课程介绍多变量微积分。内容 参数方程、极坐标。向量值函数、向量值函数微积分、立体解析几何。多变量函数、极限、连续性、偏导数、可微分性和全微分、链式法则、隐函数定理。方向导数、梯度、拉格朗日乘数。二重积分、表面面积、三重积分。线积分、格林定理、曲面积分、高斯散度定理、斯托克斯定理。
基于能量的模型的流对比估计
本文研究了一种联合估计基于能量的模型和基于流的模型的训练方法,其中两个模型基于共享的对抗值函数进行迭代更新。该联合训练方法具有以下特点:(1)基于能量的模型的更新基于噪声对比估计,流模型作为强噪声分布。(2)流模型的更新近似地最小化了流模型与数据分布之间的 Jensen-Shannon 散度。(3)与生成对抗网络(GAN)估计由生成器模型定义的隐式概率分布不同,我们的方法估计数据上的两个显式概率分布。使用所提出的方法,我们证明了流模型的综合质量的显著改进,并展示了通过学习到的基于能量的模型进行无监督特征学习的有效性。此外,所提出的训练方法可以轻松适应半监督学习。我们取得了与最先进的半监督学习方法相媲美的成果。
合作多代理增强学习中的最佳任务概括
虽然在单药强化学习(RL)的背景下广泛研究了任务概括,但在多代理RL的背景下,很少有研究。确实存在的研究通常将任务概括视为环境的一部分,当明确认为没有理论保证时。我们提出了以目标为导向的多任务多任务多代理RL(GOLEMM)的学习,该方法实现了可以证明是最佳的任务概括,据我们所知,在MARL中还没有实现。在学习了单个任意任务的最佳目标价值函数之后,我们的方法可以零弹性地推断出分布中任何其他任务的最佳策略,仅给出了每个代理的终端奖励的知识,即新任务和学习任务。从经验上我们证明,我们的方法能够概括一个完整的任务分布,而代表性基线只能学习任务分布的一小部分。
通过自学习模糊强化学习实现燃料电池混合动力汽车的终身延长能源管理策略
摘要 — 建模困难、模型时变和外部输入不确定是燃料电池混合动力汽车能源管理面临的主要挑战。本文提出了一种基于模糊强化学习的燃料电池混合动力汽车能源管理策略,以降低燃料消耗、维持电池的长期运行并延长燃料电池系统的使用寿命。模糊 Q 学习是一种无模型强化学习,可以通过与环境交互进行自我学习,因此无需对燃料电池系统进行建模。此外,燃料电池的频繁启动会降低燃料电池系统的剩余使用寿命。所提出的方法通过在强化学习的奖励中考虑燃料电池启动次数的惩罚来抑制燃料电池的频繁启动。此外,在 Q 学习中应用模糊逻辑来近似值函数可以解决连续状态和动作空间问题。最后,基于 Python 的训练和测试平台验证了所提出方法在初始状态变化、模型变化和驾驶条件变化条件下的有效性和自学习改进。