XiaoMi-AI文件搜索系统
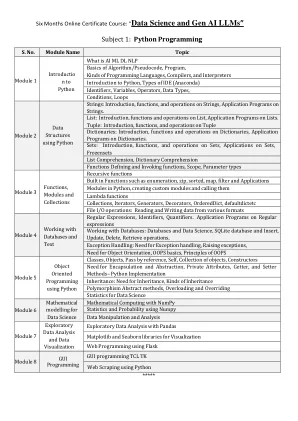
World File Search System主题1:Python编程
字符串:在字符串上的引言,功能和操作,在字符串上的应用程序。列表:列表上的简介,功能和操作,列表上的应用程序。元组:元组词典上的简介,功能和操作:词典上的简介,函数和操作,词典上的应用程序。集合:集合的简介,功能和操作,集合上的应用程序,frozensets列表理解,字典理解函数定义和调用功能,范围,参数类型
双幺正分解算法与开放量子系统模拟
对于直接实现酉门的传统量子计算机来说,模拟描述非酉演化后量子系统真实相互作用的一般量子过程是一项挑战。我们分析了有前途的方法的复杂性,例如 Sz.-Nagy 膨胀和酉函数的线性组合,它们可以通过非酉算子的概率实现来模拟开放系统,这需要多次调用编码和状态准备预言机。我们提出了一种量子二酉分解 (TUD) 算法,使用量子奇异值变换算法将具有非零奇异值的 a 维算子 A 分解为 A = ( U 1 + U 2 ) / 2,避免了经典的昂贵的奇异值分解 (SVD),其时间开销为 O(d3)。这两个酉函数可以确定性地实现,因此每个酉函数只需要调用一次状态准备预言机。对编码预言机的调用也可以显著减少,但测量误差可以接受。由于TUD方法可以将非幺正算子实现为仅两个幺正算子,因此它在线性代数和量子机器学习中也有潜在的应用。
与共同诱导的形式化图算法
≻操作员将搜索的输出限制为特定的深度。因此,上面的表达式说,在顶点a开始,重量小于15的汉密尔顿路径(在图中)分别为a:[a,b,c,d]和[a,b,c,d]和[a,c,d,b],重量为11和10。计算汉密尔顿路径的算法通常很复杂。 但是,我们的实现很简单,是由小的代数组件建立的。 有关这些组件的更多详细信息,请参见第3节。 第一个组件是∗运算符,该操作员计算传递闭合。 图 1包含其用途的图:图形是一个图形,每个顶点都具有每个可触及顶点的边缘,重量等于该顶点的最短路径上的权重之和。 例如,有一个边缘(a↦→d)∈Gragr∗,重量5,由路径a↦→c↦→d构建(请注意,在我们的形式化中,∗不是直接在图上调用,而是在图5.4中所述的理想,而是在其理想上调用)。 大多数算法“工作”都是由∗函数完成的;其余的实施是保存和过滤。 路径函数,例如,标记每个顶点的列表,代表所需的路径到达该顶点。 > =>操作员连接图形:在这里我们将其用于组合计算汉密尔顿路径的算法通常很复杂。但是,我们的实现很简单,是由小的代数组件建立的。有关这些组件的更多详细信息,请参见第3节。第一个组件是∗运算符,该操作员计算传递闭合。图1包含其用途的图:图形是一个图形,每个顶点都具有每个可触及顶点的边缘,重量等于该顶点的最短路径上的权重之和。例如,有一个边缘(a↦→d)∈Gragr∗,重量5,由路径a↦→c↦→d构建(请注意,在我们的形式化中,∗不是直接在图上调用,而是在图5.4中所述的理想,而是在其理想上调用)。大多数算法“工作”都是由∗函数完成的;其余的实施是保存和过滤。路径函数,例如,标记每个顶点的列表,代表所需的路径到达该顶点。> =>操作员连接图形:在这里我们将其用于组合
土耳其凯恩斯主义储蓄函数分析...
本研究的目的是测试凯恩斯主义储蓄函数对土耳其经济的影响。为了实现这一目标,我们利用了凯恩斯提出的基本储蓄函数,并使用了 1985 年至 2021 年土耳其经济的数据。模型中储蓄的决定因素包括人均 GDP、所得税率、存款利率和通货膨胀率。模型中选择的变量与文献一致。实证分析确定最合适的方法是自回归分布滞后 (ARDL) 方法。根据进行的实证分析,人均 GDP 和存款利率的增加会导致储蓄金额的增加。另一方面,税率和通货膨胀率的增加会减少储蓄金额。根据研究结果,凯恩斯主义储蓄函数适用于 1985 年至 2021 年的土耳其经济。
8116A 50MHz 可编程脉冲/函数发生器...
仪器背面贴有序列号牌(图 1-1 和图 1-2)。前四位数字仅在仪器发生重大修改时才会更改,后五位数字按顺序分配给仪器。本手册直接适用于标题页上引用序列号的仪器。对于序列号较高的仪器,请参阅附录 C 中的手册变更表。为了使本手册保持最新,惠普建议您定期索取最新的手册变更补充,方法是引用本手册的部件号和印刷日期,这两者都出现在标题页上,
使用实例和实体中心分割损失函数
在本文中,我们提出了一种新型的两组分损失,用于生物医学图像分割任务,称为实例和实例中心(ICI)损失,这是一种损失函数,在使用像素损失功能(例如骰子损失)时,通常会遇到实例不平衡问题。实例组件改善了具有大型和小实例的图像数据集中的小实例或“斑点”的检测。实体中心组件提高了整体检测准确性。我们使用ATLAS R2.0挑战数据集的Miccai 2022。与其他损失相比,ICI损失提供了更好的平衡分段,并以改进1的改善而显着超过了骰子损失。7-3。7%,斑点损失为0。6-5。0%的骰子相似性系数在验证和测试集中,这表明ICI损失是实例不平衡问题的潜在解决方案。关键字:实例和实体中心细分损失,细分损失。
i-motif DNA:识别,形成和细胞函数
#这些作者为这项工作做出了同样的贡献。*通信:wzhang25@njau.edu.cn(W.L.张)。抽象的i-motif(im)是一种四链(或四链体)DNA结构,它折叠了胞嘧啶(C) - 富序列。ims可以在体外的许多不同条件下折叠,这为它们在活细胞中形成的道路铺平了道路。被怀疑,IMS在各种DNA交易中起关键作用,特别是在基因组稳定性,基因转录和翻译,DNA复制,端粒和丝粒功能以及人类疾病的调节中起关键作用。我们在这里总结了用于评估IMS体外折叠的不同技术,并概述了影响其体内形成和稳定性的内部和外部因素。因此,我们描述了IM的可能生物学相关性,并提出了将其用作生物学目标的方向。关键字i -Motifs,方法论,基础修改,内部和外部条件,生物学意义突出显示 - 不同方法和分子工具的组合对于询问
在体重的代数免疫力上完全平衡函数
摘要。在本文中,我们研究了权重的代数免疫(AI)完美平衡(WPB)函数。在以前文献中显示了两类WPB函数的AI的下限后,我们证明了WPB N-可变量函数的最小AI是恒定的,对于N≥4的2。然后,我们在4个变量中计算WPB函数的AI的分布,并估计8和16个变量中的一个。对于N的这些值,我们观察到绝大多数WPB函数具有最佳的AI,并且我们无法通过随机采样来获得AI-2 WPB函数。最后,我们解决了具有有界代数免疫力的WPB函数的问题,从[GM22C]利用了构造。特别是我们提出了一种以最小AI生成多个WPB函数的方法,并且我们证明[GM22C]中表现出高非线性的WPB函数也具有最小的AI。我们以构造为WPB功能提供了较低的AI,并以AI至少N/ 2- log(n) + 1的所有元素为例。
模拟Sigmoid函数及其近似导数的设计方法
摘要 — 在本文中,我们建议使用模拟电路实现 S 型函数,该函数将用作多层感知器 (MLP) 网络神经元的激活函数,以及其近似导数。文献中已经提出了几种实现方法,特别是 Lu 等人 (2000) 的实现方法,他们提供了采用 1.2 µ m 技术实现的可配置简单电路。在本文中,我们展示了基于 Lu 等人的 S 型函数电路设计,使用 65 nm 技术以降低能耗和电路面积。该设计基于对电路的深入理论分析,并通过电路级模拟进行验证。本文的主要贡献是修改电路的拓扑结构以满足电路所需的非线性响应以及提取所得电路的直流功耗。索引词——激活函数、模拟 CMOS 电路、近似导数、反向传播、多层感知器、S 型函数。