XiaoMi-AI文件搜索系统
World File Search System区分
AI 蛇油：人工智能能做什么，不能做什么，以及如何区分 - 第 1 章
想象一个平行宇宙，人们没有专门用来形容不同交通方式的词语，只有集合名词“交通工具”。他们用这个词来指汽车、公共汽车、自行车、宇宙飞船以及从 A 地到 B 地的所有其他交通方式。这个世界上的对话令人困惑。人们就交通工具是否环保展开了激烈的争论，但没人意识到争论的一方在谈论自行车，而另一方在谈论卡车。火箭技术取得了突破，但媒体的焦点是交通工具如何变得更快，因此人们打电话给汽车经销商（哦，汽车经销商）询问何时会有更快的车型。与此同时，欺诈者利用消费者在交通工具技术方面不知道该相信什么的事实，因此交通工具行业诈骗猖獗。现在，将“汽车”一词替换为“人工智能”，我们就很好地描述了我们生活的世界。人工智能（简称 AI）是一组松散相关技术的总称。ChatGPT 与银行用来评估贷款申请人的软件几乎没有共同之处。两者都被称为 AI，但在所有重要方面——如何
与无荡险密码学的应用同时无法区分性
无统治的密码学关注的是利用无关原则来构建否则不可能实现经典实现的加密原则。理解不统治的加密的可行性，这是一个关键的不统一的基础之一，满足普通模型中无法区分的安全性是该地区的一个主要开放问题。到目前为止，无统治加密的现有构造要么在量子随机甲骨文模型中，要么基于新的猜想。我们提出了一种新的方法来通过简化有关非本地量子状态歧视的新奇问题来进行无统治的加密方法：非沟通（但纠结）的玩家如何区分不同的分布而不是量子状态？我们将此任务同时称为状态。我们的主要技术结果表明，玩家无法区分每个接收独立选择的HAAR随机状态与所有接收相同HAAR随机状态的玩家。我们利用此结果在平原模型中使用量子解密密钥的首次构建不可吻合的加密可满足不合格性的安全性。我们还对单分隔符的加密和泄漏 - 弹性的秘密共享显示了其他影响。
使用基于实验室的高光谱图像和机器学习来区分开花蓝细菌：在环境范围内对有毒物种的验证
蓝细菌是内陆水域藻类开花的主要因素，威胁生态系统功能和用水的用途，尤其是在产生毒素的菌株占主导地位时。在这里，我们检查了140个高光谱（HS）图像，这些代表的五个代表，可能是毒素产生和盛开的属属微囊藻，浮游生物，浮游生物，阿法尼兹瘤，菊花菌，菊花菌和dolichospermum，以确定可见和近距离散布的潜在的（以/nirir的范围）的潜在。培养物在各种光和营养条件下生长，以诱导各种色素和光谱变异性，模仿自然环境中可能发现的变化。重要的是，我们假设了一个简化的方案，其中所有光谱变异性均来自蓝细菌。在整个蓝细菌生命周期中，获得了多个HS图像以及叶绿素A和植物蛋白酶的提取。图像，并使用K-均值算法提取来自感兴趣区域的平均光谱。使用七种方法对光谱数据进行了处理，以随后整合到随机森林模型中，其性能通过训练，验证和测试集的不同指标进行了评估。使用第一或第二个衍生物以及光谱平滑的成功分类率接近90％，并确定VIS和NIR中的重要波长。微囊孢子和Chrysosporum是达到最高精度（> 95％）的属，其次是浮游生物（79％），最后是Dolichospermum和Aphanizomenon（> 50％）。HS图像对
如何使用量子不可区分混淆
量子复制保护由 Aaronson [ 1 ] 提出，它能够给出无法被有效复制的量子程序描述。尽管经过十多年的研究，但人们知道只有极少数程序能够实现复制保护。作为我们的第一项贡献，我们展示了如何为所有程序实现“最佳”复制保护。我们通过引入量子态不可区分混淆 ( qsiO ) 来实现这一点，这是用于经典程序量子描述的混淆概念。我们表明，将 qsiO 应用于程序可立即实现最佳复制保护。我们的第二项贡献是表明，假设存在单向注入函数，qsiO 是一大类可穿孔程序的具体复制保护 — — 大大扩展了可复制保护程序的类别。我们证明中的一个关键工具是不可克隆加密 (UE) 的新变体，我们称之为耦合不可克隆加密 (cUE)。虽然在标准模型中构建 UE 仍然是一个重要的未解决的问题，但我们能够从单向函数构建 cUE。如果我们另外假设 UE 的存在，那么我们可以进一步扩展 qsiO 是复制保护的可穿孔程序类。最后，我们相对于一个有效的量子预言机构建 qsiO。
如何使用量子不可区分混淆
量子复制保护由 Aaronson [ Aar09 ] 提出，它可以给出无法被有效复制的量子程序描述。尽管经过十多年的研究，但已知复制保护仅对非常有限的一类程序可用。作为我们的第一项贡献，我们展示了如何为所有程序实现“最佳”复制保护。我们通过引入量子态不可区分混淆 ( qsiO ) 来实现这一点，这是用于经典程序量子描述的混淆概念。我们表明，将 qsiO 应用于程序可立即实现最佳复制保护。我们的第二项贡献是表明，假设存在单向注入函数，qsiO 是一大类可穿孔程序的具体复制保护 — — 大大扩展了可复制保护程序的类别。我们证明中的一个关键工具是不可克隆加密 (UE) 的新变体，我们称之为耦合不可克隆加密 (cUE)。虽然在标准模型中构建 UE 仍然是一个重要的未解决的问题，但我们能够从单向函数构建 cUE。如果我们另外假设 UE 的存在，那么我们可以进一步扩展 qsiO 是复制保护的可穿孔程序类。最后，我们相对于有效的量子预言机构建 qsiO。
通过肠道菌群区分轻度和重度疾病
1数学生物学与生物信息学系系统生物学和医学研究所，莫斯科117246，俄罗斯； fedorov.de@gmail.com（D.E.F.）; hed.robin@gmail.com（e.v.s.）; paraslonic@gmail.com（a.i.m.）; pavav@mail.ru（A.V.P。）2洛普金联邦研究和联邦医学生物机构物理医学临床中心，莫斯科119435，俄罗斯； ks-selezneva@yandex.ru（O.V.S.）; ppp843@yandex.ru（K.M.K.）; djdf26@gmail.com（v.a.v.）; maxim_d_morozov@mail.ru（M.D.M.）3莫斯科州立医学院哥伦斯大学临床牙科系，莫斯科127473，俄罗斯； olegyanushevich@yandex.ru（O.O.Y。 ）; krikheli_msu@mail.ru（N.I.K. ）; truovl@gmail.com（O.V.L. ）; dna-mit8@mail.ru（D.N.A。 ）; phlppsokolov@gmail.com（F.S.S. ）; docfomenko@yandex.ru（a.k.f. ）; devkota@bk.ru（M.K.D. ）; nicdoctor2009@yandex.ru（N.G.A。 ）; azabor@mail.ru（A.V.Z。 ）; pbely@ncpharm.ru（P.A.B. ）; sergiotsar@yandex.ru（s.v.t. ）; vvevdokimov@rambler.ru（v.v.e。 ）; igormaev@rambler.ru（i.v.m. ）; vgovorun@yandex.ru（v.m.g。） *通信：olgagaleeva546@gmail.com（J.S.G. ）; ilinaen@gmail.com（E.N.I.）3莫斯科州立医学院哥伦斯大学临床牙科系，莫斯科127473，俄罗斯； olegyanushevich@yandex.ru（O.O.Y。）; krikheli_msu@mail.ru（N.I.K.）; truovl@gmail.com（O.V.L.）; dna-mit8@mail.ru（D.N.A。）; phlppsokolov@gmail.com（F.S.S.）; docfomenko@yandex.ru（a.k.f.）; devkota@bk.ru（M.K.D.）; nicdoctor2009@yandex.ru（N.G.A。）; azabor@mail.ru（A.V.Z。）; pbely@ncpharm.ru（P.A.B.）; sergiotsar@yandex.ru（s.v.t.）; vvevdokimov@rambler.ru（v.v.e。）; igormaev@rambler.ru（i.v.m.）; vgovorun@yandex.ru（v.m.g。）*通信：olgagaleeva546@gmail.com（J.S.G.）; ilinaen@gmail.com（E.N.I.）
![b'B'The分数量子厅（FQH）状态是物质拓扑阶段的一些最佳研究的例子。它们的特征是各种拓扑数量，例如准颗粒电荷，霍尔电导，霍尔粘度和边缘理论的手性中心电荷，这从根本上是由电子之间的非平凡相关性引起的。这些状态中相关性的一种特别用途是\ xe2 \ x80 \ x9cguiding Center \ xe2 \ x80 \ x80 \ x9d静态结构因子\ xc2 \ xaf s（k），它在长波长的the translation and-In-insementies [1，2]中，在长波长度上是四分之一的。 A fundamental feature of the FQH ground states is that the fourth rank tensor that determines this quartic term satisfies the so called \xe2\x80\x9cHaldane bound\xe2\x80\x9d [ 2 , 3 ] , a lower bound on the strength of long-wavelength density fluctuations in terms of the Hall viscosity tensor [ 4 , 5 ] .在旋转不变的情况下，当指南中心静态结构因子和霍尔粘度张量的四分之一项都由一个pa-rameter确定时，界限可以表示为两者之间的简单标量不平等。在物理层面上，它可以理解为将QH状态与拓扑琐碎的产物状态态区分开的相关性最小的存在，即前者不能绝步地变形到后者。 FQH上的大量工作涉及一类旋转不变的模型wave](/simg/c/c60171978270993a15b3267b52b0da3abc5d5b5e.webp)
b'B'The分数量子厅（FQH）状态是物质拓扑阶段的一些最佳研究的例子。它们的特征是各种拓扑数量，例如准颗粒电荷，霍尔电导，霍尔粘度和边缘理论的手性中心电荷，这从根本上是由电子之间的非平凡相关性引起的。这些状态中相关性的一种特别用途是\ xe2 \ x80 \ x9cguiding Center \ xe2 \ x80 \ x80 \ x9d静态结构因子\ xc2 \ xaf s（k），它在长波长的the translation and-In-insementies [1，2]中，在长波长度上是四分之一的。 A fundamental feature of the FQH ground states is that the fourth rank tensor that determines this quartic term satisfies the so called \xe2\x80\x9cHaldane bound\xe2\x80\x9d [ 2 , 3 ] , a lower bound on the strength of long-wavelength density fluctuations in terms of the Hall viscosity tensor [ 4 , 5 ] .在旋转不变的情况下，当指南中心静态结构因子和霍尔粘度张量的四分之一项都由一个pa-rameter确定时，界限可以表示为两者之间的简单标量不平等。在物理层面上，它可以理解为将QH状态与拓扑琐碎的产物状态态区分开的相关性最小的存在，即前者不能绝步地变形到后者。 FQH上的大量工作涉及一类旋转不变的模型wave
b'B'The分数量子厅（FQH）状态是物质拓扑阶段的一些最佳研究的例子。它们的特征是各种拓扑量，例如准粒子电荷，霍尔电导，霍尔的粘度和边缘理论的手性中心电荷，这从根本上是由电子之间的非平凡相关性引起的。在这些状态下相关性的一种特别用途是\ xe2 \ x80 \ x9cguiding Center \ xe2 \ x80 \ x80 \ x9d静态结构因子\ xc2 \ xaf s（k），在长波长的情况下，在平移和In-in-in-in-in-in-in-in-in-in-in-in-in-in-in-in-in-in-in-in-nimememementscements中是四分之一的Quartic [k）。FQH接地的一个基本特征是，确定此四分之一术语的第四个等级张量满足所谓的\ xe2 \ x80 \ x9Chaldane绑定\ Xe2 \ x80 \ x80 \ x9d [2，3]，较低的结合在长波长度的强度下，构成了hall [4 hall sects of Hall ted the the Hall [4 hall [4 hall]的强度。在旋转不变的情况下，当引导中心静态结构因子和霍尔粘度张量的四分之一项都由每个pa-rameter确定时，界限可以表示为两者之间的简单标量不平等。在物理层面上，可以理解为将QH状态与拓扑琐碎的产物状态区分开的相关性最小的存在，即，前者不能绝热地变形到后者。在FQH上进行了许多工作，涉及一类旋转不变的模型波函数（Laughlin [6]，Moore-Read [7]，Read-Rezayi [8]），与欧几里得的保形场理论有关，并使Haldane结合饱和[9，10]。这些模型状态是属于某些非常特殊模型的汉密尔tonians的最高密度状态（零能量特征态），并且在理解FQHE方面发挥了关键作用。他们非常特殊的功能之一是，它们是\ xe2 \ x80 \ x9cmaxmaximally手性\ xe2 \ x80 \ x9d，因为它们在圆柱形几何形状中仅包含一个与半融合状态相对于一个cut的圆柱状态的贡献。这是\ xe2 \ x80 \ x9cmaximal手性\ xe2 \ x80 \ x9d的非常强烈的条件：最大性手性的较弱版本是，纠缠谱的低较低部分（或同等地，拓扑模式）仅具有一种chirality的贡献。这个较弱的版本通常会被汉密尔顿人的基础状态所满足，而汉密尔顿人的基础状态却远离模型。在本文中，我们解决了一个问题 - 饱和hal -dane结合需要什么条件？我们在附录B中显示，连续旋转不变性是必需的。之所以如此，是因为角动量的波动有助于O（K \ Xe2 \ X84 \ X93）4的静态结构因子4，但对HALL粘度张量不足。对于旋转不变的系统，先前已显示[11 \ xe2 \ x80 \ x93 13]，即\ xce \ xbd \ xbd \ xe2 \ x88 \ x92 = p /（2 np \ xe2 \ xe2 \ x88 \ x92 1）jain状态[14]不满意，不满意n> 1，不满足n> 1，不满意 任何一个。这些FQH状态包含旋转不变的基态上方的Spin-2重力激发的两种手势。特别是一些研究支持了后者[9]。这会导致长波长的静态结构因子的相关性比霍尔粘度的大小所需的更大的相关性。但是，尚不清楚是否需要强大的最大性手性或较弱的版本足以使各向同性FQH状态的结合饱和。我们以数值调查了这个问题，并提供了明确的证据，表明弱的最大手性不足。因此，我们期望只有理想的保形块波形饱和haldane结合。我们使用旋转不变的二维Hamilto-Nians在\ xce \ xbd = 1 / 3,1 / 5和2/5的FQH状态的长波长极限中计算静态结构因子。为此，我们在圆周的无限缸[15]上使用密度矩阵重新归一化组，并通过考虑大的l y /\ xe2 \ x84 \ x93来接近2D-LIMIT。我们计算O（K \ Xe2 \ X84 \ X93）的系数\ XC2 \ Xaf S 4）4项在指南中心静态结构因子的长波长膨胀中，并表明它比Haldane绑定的Haldane by by for Haldane by to haldane by to for for for Haldane to for Haldane to for Haldane to for for for f q QH的Haldane Hamiltonians的FQH地面。我们通过分析围绕模型'
在常染色体显性和零星阿尔茨海默氏病中区分淀粉样ββ
淀粉样蛋白β沉积是散发性阿尔茨海默氏病和常染色体主导的阿尔茨海默氏病的标志性病变之一，后者是由淀粉样蛋白β处理中涉及的基因突变引起的。尽管淀粉样蛋白β沉积是散发性阿尔茨海默氏病和常染色体主导的阿尔茨海默氏病的核心，但这些阿尔茨海默氏病亚型的某些差异在与淀粉样ambeta的空间模式方面存在观察到。Previous work has shown that the spatial pattern of amyloid-beta in individuals spanning the sporadic Alzheimer ' s disease spectrum can be reproduced with high ac- curacy using an epidemic spreading model which simulates the diffusion of amyloid-beta across neuronal connections and is constrained by individual rates of amyloid-beta production and clearance.然而，尚未研究是否可以以相同的方式对稀有的常染色体式阿尔茨海默氏病中的淀粉样蛋白-Beta沉积进行建模，如果是这样，如果是这样，淀粉样蛋白贝塔（Alzheimer）的淀粉样蛋白β的传播模式多么一致。我们利用流行病扩散模型作为数据驱动的方法，用于探测淀粉样蛋白β的传播模式在三个不同的大型成像数据集中的淀粉样蛋白β传播模式（2种散发性阿尔茨海默氏病，1个常染色体典型的阿尔茨海默氏病）。我们分别评估了每个数据集中的个体和个体内模型性能，并进一步识别了淀粉样蛋白β扩散的最可能受试者特异性的表述。我们将流行病扩散模型分别应用于阿尔茨海默氏病神经影像学计划（n = 737），开放式成像研究系列（n = 510）和主要遗传的阿尔茨海默氏症网络（n = 249），其中后两个使用相同的管道处理。使用在零星阿尔茨海默氏病的先前作品中定义的epcentres，流行病扩散模型对所有三个数据集中的淀粉样蛋白β沉积的区域模式进行了适度的预测。我们进一步发现，虽然大多数淀粉样蛋白β的最有可能的中心 - 积极对象与默认模式网络重叠，但常染色体占主导地位的13％
Haruna GS等。研究了Aloxan诱导的糖尿病白化病大鼠阳离子甲醇提取物的抗糖尿病潜力。 Clin J Dia Care Control 2024，6（1）：180049。 smita r和kochar是。儿童中的拉达：是时候重新思考了。 Clin J Dia Care Control 2024，6（1）：180045。 Mahmood Arifa和Sawai Ma。电纺纳米纤维在牙周炎治疗中的新兴作用。牙科和凹痕练习J 2025，7（1）：180095。 Joseph S等。医疗保健提供者中无菌非接触技术临床实践框架的知识，态度和实践：系统审查协议。 ADV护理患者护理INT J 2023，6（1）：180067。 Katikar M和Abhishek BP。将获得的童年失语症与发育语言障碍区分开来。 Acta Neurophysiol 2025，6（1）：180097。
糖尿病是一个严重的全球健康问题，其特征是高血糖，是由胰岛素的绝对或相对缺乏或细胞水平上的胰岛素抵抗引起的。这项研究的目的是研究白化大鼠中grandiflora的甲醇茎皮的抗糖尿病潜力。使用标准方法确定植物化学分析，α淀粉酶和α葡萄糖酶抑制活性以及葡萄糖浓度。二十只白化大鼠被随机分为五组四只大鼠，每组1是正常对照，用糖尿病诱导了组2，未接受治疗，用Glibenclamide诱导并用Glibenclamide诱导第4组，第4组和5组被诱导并用提取物进行100天和血液限制的次数（分别为100 mgkk-1），将所有次数切成三天的间隔。结果表明，不存在酚类，碳水化合物和单宁酸，类黄酮中等量，而类固醇，皂苷，萜烯，甘氨酸，蒽醌和心脏糖苷则没有。与A. grandiflora提取物相比，标准药物Glibenclamide（98.06％）和二甲双胍（96.77％）显示出更高的α淀粉酶抑制活性。样品的5.0mg浓度显示（79.53％）抑制作用。在30.0mg/ml的样品（98.70％）中具有显着（P <0.05）的抑制作用（p <0.05），而标准药物（Glibenclamide）（Glibenclamide）（84.88％）抑制蛋白和二甲双胍表现出（88.22％）抑制性活性（88.22％）。显着（p <0.05）在治疗组中血清葡萄糖的降低显着，而（第2组）在所有大鼠中均表现出持续的糖尿病状态，证实了甲醇提取物的抗糖尿病特性。
定量MRCP将恶性与良性区分开来...
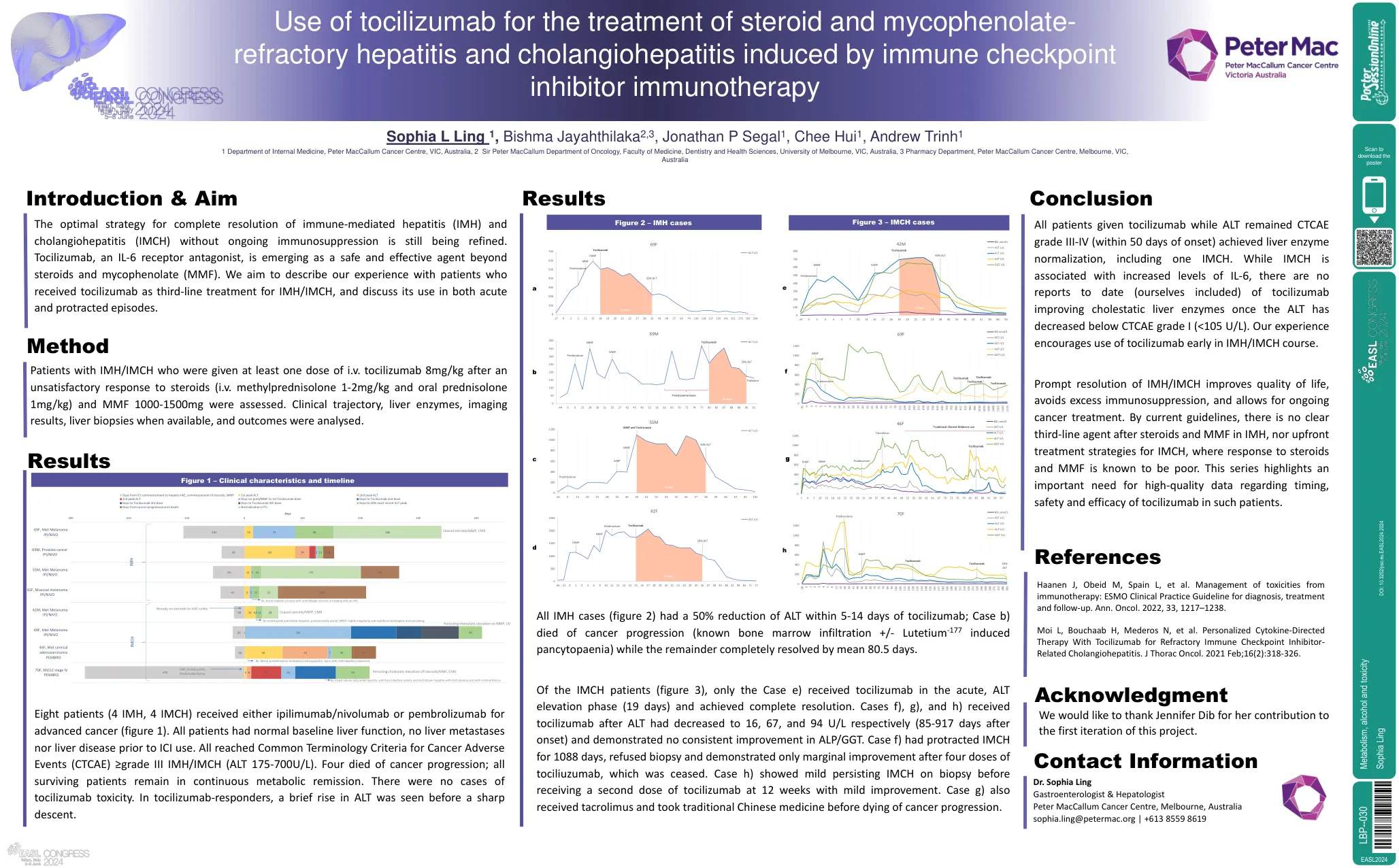
IMCH患者的（图3），仅此病例E）在急性，ALT升高阶段（19天）接受了弓形虫，并实现了完全分辨率。 病例f），g）和h）在ALT降低到16、67和94 U/L（发病后85-917天）后接受毒珠，并且在ALP/GGT方面没有一致的改善。 案例f）持续了1088天，拒绝活检，仅在四剂tociliuzumab停止后才证明了边缘改善。 案例H）在活检中显示出轻度的持续iMch，然后在12周时接受第二剂托曲珠单抗，并有温和的改善。 病例G）还接受了他克莫司，并在死亡癌症进展之前服用了中药。（图3），仅此病例E）在急性，ALT升高阶段（19天）接受了弓形虫，并实现了完全分辨率。病例f），g）和h）在ALT降低到16、67和94 U/L（发病后85-917天）后接受毒珠，并且在ALP/GGT方面没有一致的改善。案例f）持续了1088天，拒绝活检，仅在四剂tociliuzumab停止后才证明了边缘改善。案例H）在活检中显示出轻度的持续iMch，然后在12周时接受第二剂托曲珠单抗，并有温和的改善。病例G）还接受了他克莫司，并在死亡癌症进展之前服用了中药。