XiaoMi-AI文件搜索系统
World File Search System奥地利生物医学工程学会(ÖGBMT)年会
1 自动检测镫骨肌反射以进行客观人工耳蜗植入 Celine Desoyer, C. Baumgartner 2 研究脑组织模拟水凝胶的微流体灌注多孔行为 Marcel Horn, MP Kainz, M. Terzano, GA Holzapfel 3 可植入水凝胶的形态变化 Luca Kalchgruber, M. Polz, C. Baumgartner 4 A1 腺苷受体在星形胶质细胞中诱发的 Ca2+ 信号 Filip Kienleitner, K. Lenk 5 谷氨酸转运蛋白密度对衰老过程中星形胶质细胞钙动力学的影响 Melanie Anna Koch, K. Lenk 6 使用随机上下文无关语法进行 miRNA 预测 Daniel Schulhofer 7 基于 PVA 的组织模拟水凝胶的压缩-拉伸特性 Manuel Steinberger, MP Kainz, M. Terzano, GA Holzapfel 8 简化头部模式下光电植入物皮层刺激的计算研究 Vincent Thomas Valente, T. Rienmüller
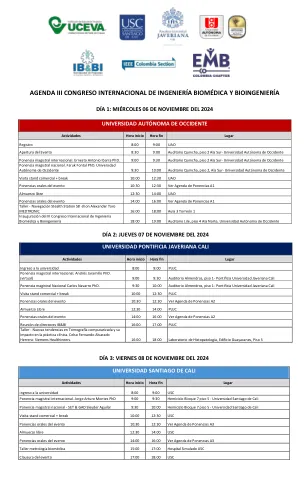
第三届生物医学工程与生物工程国际大会议程
活动口头报告 14:00 16:00 查看报告议程 A1 研讨会 - 隐形站导航 S8 -Jhon Alexander Toro MEDTRONIC 16:00 18:00 教室 3 塔 1 第三届国际生物医学工程和生物工程大会开幕式 18:00 19:00 西方自治大学北翼 4 楼 Lile 礼堂
M. Tech的书面测试教学大纲。 (生物医学工程...
M. Tech的书面测试教学大纲。(生物医学工程)入学AY 2024-25书面测试将有以下六个部分,候选人必须选择这六(6)个部分中的任何两个(2)个部分进行考试:1。生物学2。化学3。物理4。数学5。生理学6。工程(A或B节)。选择工程部分的候选人必须选择A或b节。只能尝试和评估候选人选择的两个部分(例如:生物学和工程部分A,化学和物理学,生理学和工程款B等)。每个部分的试卷将包括10个问题,每个问题分别1个。不会有负标记。将允许在书面测试期间使用科学计算器,候选人应带上自己的科学计算器(手机等。将不允许)。每个部分的教学大纲将达到与GATE 2024检查或等效测试/考试相当的水平。下面给出了每个部分的教学大纲:
3D打印在生物医学工程中的应用
摘要 - 这篇全面的审查论文封装了3D印刷在生物医学工程中的变革性影响,阐明了关键发现和贡献,这些发现和贡献强调了其在革新医疗保健方面的重要性。患者特异性植入物,假肢和矫形器的出现已成为标志性的成就,为个别患者提供了优化的舒适性和功能。手术精度已通过使用解剖上精确的3D打印模型细致的计划提升,从而大大降低了风险和并发症。定制的药物输送系统预示着个性化医学的新时代,确保了精确的给药和最小的副作用。生物打印技术已通过成功打印出功能组织和器官的重生医学的潜力,这有望在移植和组织修复方面取得突破。在牙科和颌面外科的领域中,3D打印简化了程序,提供定制的解决方案并改变了患者的生活质量。本评论强调了3D打印对医疗保健的深远影响,提供了个性化,精确且有效的医疗干预措施,为改善患者结果提供了巨大的承诺。
课程名称:BME1560 生物医学工程人工智能(2022 年秋季)
课程描述:本课程为研究生提供在机器学习和深度学习领域应用生物医学应用的广度和深度。本课程首先介绍基本的机器学习算法,包括监督学习(例如逻辑回归、朴素贝叶斯、决策树等)和无监督学习(k-means、层次聚类)。随后将描述其他基本概念,例如分类器评估和统计测试以比较分类器。下一部分是研究用于各种生物医学应用的不同深度学习模型(研讨会形式),处理多种类型的数据,包括但不限于生物信号、生理数据、环境数据、语音、文本、图像和视频。将讨论用于顺序和非顺序数据的不同类型的监督和非监督框架,包括前馈神经网络、卷积神经网络、自动编码器、长短期记忆、时间卷积网络。在最后一部分,将讨论应用于生物医学应用的高级深度学习架构,包括生成对抗网络和对比学习。本课程将包括编程作业(2)、论文评论和小组项目(1-3 人团队)。
卡尔加里大学第十六届年度生物医学工程...
会议 1 - 人类活动 (KNB 214) 会议主席:Karson Fitzsimons 评委:Kirsten Bott 和 Sam Leech 9:20 - 前臂拐杖长度对上肢运动学的影响 演讲者:Amanda Chen 指导老师:Ranita Manocha 博士 9:30 - 周期性负荷中断对牛皮质骨的影响 演讲者:Tudor Muresan 指导老师:Brent Edwards 博士 9:40 - pH 值的变化如何影响肌联蛋白中的应激?演讲者:Nikhil Srivalsan 主管:Walter Herzog 博士 9:50 – 胫骨加速度不是预测肌肉骨骼负荷的有效替代测量指标 演讲者:Jean Tu 主管:Brent Edwards 博士 10:00 – 脑瘫儿童剥皮肌肉纤维的主动力 演讲者:Gavin Thomas 主管:Venus Joumaa 博士和 John Holash 博士 10:10 – 整理支撑:预测马的肌腱拉伤 演讲者:Sammy Patwary 主管:John Bertram 博士 10:20 – 研究免疫荧光标记的骨骼兔腰肌肌节长度不均匀性和力量 演讲者:Dhairya Desai 主管:Walter Herzog 博士 10:30 – 延迟 3 周益生元纤维干预对脂肪的影响雌性斯普拉格道利大鼠股外侧肌的浸润 演讲者:Arman Murani 主管:Walter Herzog 博士
第24届艾伯塔省生物医学工程会议...
Sergei Gasilov的高级科学家,加拿大光源Sergey Gasilov是加拿大光源的高级科学家,专门从事仪器和技术的开发,用于硬X射线成像和微视频学。他毕业于莫斯科工程物理研究所,后来又在俄罗斯,意大利,日本,法国和德国工作,从而使用不同的X射线来源进行相比的X射线成像。 在他的博士后研究期间,谢尔盖(Sergey)开发了折射成像技术的硬X射线指数,用于对欧洲同步加速器辐射设施的大型生物医学标本进行层析成像检查。 后来,谢尔盖(Sergey)在ANKA同步器源构建了硬X射线成像光束线和显微镜站。 自2018年以来,谢尔盖(Sergey)负责加拿大光源的生物医学成像和疗法(BMIT)束线。 来自加拿大和国外的生物医学研究人员和物质科学家应用BMIT的最先进的工具和软件工具,用于对位于现场,室内和现场的各种标本的3D非破坏性成像。他毕业于莫斯科工程物理研究所,后来又在俄罗斯,意大利,日本,法国和德国工作,从而使用不同的X射线来源进行相比的X射线成像。在他的博士后研究期间,谢尔盖(Sergey)开发了折射成像技术的硬X射线指数,用于对欧洲同步加速器辐射设施的大型生物医学标本进行层析成像检查。后来,谢尔盖(Sergey)在ANKA同步器源构建了硬X射线成像光束线和显微镜站。自2018年以来,谢尔盖(Sergey)负责加拿大光源的生物医学成像和疗法(BMIT)束线。来自加拿大和国外的生物医学研究人员和物质科学家应用BMIT的最先进的工具和软件工具,用于对位于现场,室内和现场的各种标本的3D非破坏性成像。
M.Sc.生物医学工程与医学物理(BEMP)M ...modulhandbuch
研究/考试服务的描述:考试表现包括对英语学士学位论文的科学阐述,该论文是由参与课程学院的大学讲师发行和监督的(主题)。与主题演员同意的德语准备工作应根据考试委员会要求或主题。学生使用在课程中获得的专家和方法知识来处理航空航天领域的科学,特定工程或应用科学问题。必须观察到慕尼黑的各个主席的正式要求和“确保良好科学实践的准则”。指南:https://portal.mytum.de/ archive/commendium_rechts excalse/other/wiss_fehlenbalge.pdf/查看处理时间为6个月。书面阐述通常应包含以下各节:引言,问题和客观,理论基础,方法,结果,摘要和书目附录。主题演员或在交货前澄清主题的主题。提交科学工作的提交补充了口头表现,该陈述不是分别分别分级的。
CRISPR-CAS技术在生物医学工程中的应用概述
1 <部门,哈马丹医学院医学院,哈马丹,伊朗2伊朗Zanjan医学科学大学,伊朗5 INSERM-S-MD 1197/武装部队部,武装部队生物医学研究所(IRBA),Paul-Brousse医院Villejuif和CTSA Clamart,法国CTSA Clamart,法国6 Sivancell 6 Sivancell,Sivan Aryo Pharmen fulling tehran,Tehran,iran fullan iran fulleran irantaran,iran erantaran irantaran,iran rutial erantaran irrator,美国加利福尼亚州洛杉矶的南加州大学生物化学与分子生物学9 9应用微生物技术系,生物技术与生命科学学院,苏霍大学,库玛莫托,日本,<部门,哈马丹医学院医学院,哈马丹,伊朗2伊朗Zanjan医学科学大学,伊朗5 INSERM-S-MD 1197/武装部队部,武装部队生物医学研究所(IRBA),Paul-Brousse医院Villejuif和CTSA Clamart,法国CTSA Clamart,法国6 Sivancell 6 Sivancell,Sivan Aryo Pharmen fulling tehran,Tehran,iran fullan iran fulleran irantaran,iran erantaran irantaran,iran rutial erantaran irrator,美国加利福尼亚州洛杉矶的南加州大学生物化学与分子生物学9 9应用微生物技术系,生物技术与生命科学学院,苏霍大学,库玛莫托,日本,<部门,哈马丹医学院医学院,哈马丹,伊朗2伊朗Zanjan医学科学大学,伊朗5 INSERM-S-MD 1197/武装部队部,武装部队生物医学研究所(IRBA),Paul-Brousse医院Villejuif和CTSA Clamart,法国CTSA Clamart,法国6 Sivancell 6 Sivancell,Sivan Aryo Pharmen fulling tehran,Tehran,iran fullan iran fulleran irantaran,iran erantaran irantaran,iran rutial erantaran irrator,美国加利福尼亚州洛杉矶的南加州大学生物化学与分子生物学9 9应用微生物技术系,生物技术与生命科学学院,苏霍大学,库玛莫托,日本,<部门,哈马丹医学院医学院,哈马丹,伊朗2伊朗Zanjan医学科学大学,伊朗5 INSERM-S-MD 1197/武装部队部,武装部队生物医学研究所(IRBA),Paul-Brousse医院Villejuif和CTSA Clamart,法国CTSA Clamart,法国6 Sivancell 6 Sivancell,Sivan Aryo Pharmen fulling tehran,Tehran,iran fullan iran fulleran irantaran,iran erantaran irantaran,iran rutial erantaran irrator,美国加利福尼亚州洛杉矶的南加州大学生物化学与分子生物学9 9应用微生物技术系,生物技术与生命科学学院,苏霍大学,库玛莫托,日本,<部门,哈马丹医学院医学院,哈马丹,伊朗2伊朗Zanjan医学科学大学,伊朗5 INSERM-S-MD 1197/武装部队部,武装部队生物医学研究所(IRBA),Paul-Brousse医院Villejuif和CTSA Clamart,法国CTSA Clamart,法国6 Sivancell 6 Sivancell,Sivan Aryo Pharmen fulling tehran,Tehran,iran fullan iran fulleran irantaran,iran erantaran irantaran,iran rutial erantaran irrator,美国加利福尼亚州洛杉矶的南加州大学生物化学与分子生物学9 9应用微生物技术系,生物技术与生命科学学院,苏霍大学,库玛莫托,日本,
第 25 届年度阿尔伯塔生物医学工程会议...
Sabina Bruehlmann Nimble Science 首席执行官 Christian Clermont 加拿大阿尔伯塔体育学院高级研究员 Abhilash Hareendranathan MEDO.ai Inc. 前研发主管 Emily Matijevich Orpyx Medical Technologies 生物识别和应用研究总监