XiaoMi-AI文件搜索系统
World File Search System标量弹性动力学与非厄米量子力学的联系
近年来,量子理论与弹性动力学(一种从现象学角度描述材料随时间变化的宏观响应的理论)之间的思想交流十分活跃。在这里,我们开辟了一条从非厄米量子力学中转移更多工具的途径。我们首先确定一维无体力弹性动力学方程与时间无关的薛定谔方程之间的异同,并找出两者等价的条件。随后,我们展示了非厄米微扰理论在确定弹性系统响应中的应用;使用量子力学方法计算具有开放边界的异质固体中的泄漏模式和能量衰减率;以及在这些组件的光谱中构建简并性。后者的结果可能具有技术意义,因为它引入了一种通过在简单的弹性系统中设计它们来利用与非厄米简并性相关的异常波动现象的方法,用于实际设备。作为此类应用的一个示例,我们展示了如何利用简并异常点附近的独特拓扑结构,将按照我们的方案设计的具有两个简并剪切状态的弹性板组件用于增强灵敏度的质量传感。
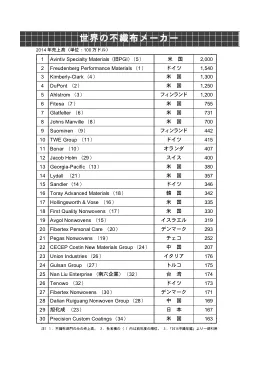
1 Avintiv Specialty Materials (旧PGI)(5) 米 国 ...
1 Avintiv Specialty Materials ( 旧 PGI )( 5 ) 米 国 2,000
超导量子比特的非厄米动力学中的量子跳跃
耗散在自然界中普遍存在;例如原子核的放射性衰变和吸收介质中的波传播,耗散是这些系统与不同环境自由度耦合的结果。这些耗散系统可以用有效非厄米汉密尔顿量进行现象学描述,其中引入非厄米项来解释耗散。非厄米性导致复杂的能谱,其虚部量化系统中粒子或能量的损失。非厄米汉密尔顿量的简并性称为异常点 (EP),其中特征值和相关的特征态合并 [1,2]。许多经典系统 [3-11] 已证明有效哈密顿的存在,并应用于激光模式管理 [12-14]、增强传感 [15-20] 和拓扑模式传输 [21-24]。尽管有效哈密顿方法是几十年前作为量子测量理论的一部分发展起来的,但最近对单电子自旋 [25,26]、超导量子比特 [27] 和光子 [28-30] 的实验扩大了人们对非厄米动力学中独特量子效应的兴趣。已经采用两种方法来研究量子区域内的非厄米动力学。第一种方法是通过将非厄米哈密顿量嵌入到更大的厄米系统中 [25,26,30],通过称为哈密顿膨胀的过程来模拟这些动力学。第二种方法是将非厄米动力学直接从耗散量子系统中分离出来 [27] 。为了理解这种方法,回想一下耗散量子系统通常用包含两个耗散项的林德布拉德主方程来描述:第一个项描述系统能量本征态之间的量子跳跃,第二个项产生相干非幺正演化 [31 – 33] 。通过抑制前一个项,得到的演化是
非厄米物理的非幺正量子行走方法
[1] K. Mochizuki, D. Kim, 和 H. Obuse, Phys. Rev. A 93 , 062116 (2016)。[2] L. Xiao, X. Zhan, ZH Bian, KK Wang, X. Zhang, XP Wang, J.Li, K. Mochizuki, D. Kim, N. Kawakami,Y. Wi, H. Obuse, B. Sanders, P. Xue, Nature Phys. 13 , 1117 (2017)。[3] L. Xiao, X. Qin, K. Wang, Z. Bian, X. Zhan, H. Obuse, B.Sanders, W. Yi, P. Xue, Phys. Rev. A 98 , 063847 (2018)。[4] K. Mochizuki, D. Kim, N. Kawakami, 和 H. Obuse, Phys. Rev. A, 102 , 062202 (2020)。[5] M. Kawasaki、K. Mochizuki、N. Kawakami 和 H. Obuse, Prog. Theor. Exp. Phys. 2020 , 12A105 (2020)。[6] N. Hatano 和 H. Obuse, Annals of Physics 435, 168615 (2021)。[7] T. Bessho、K. Mochizuki、H. Obuse 和 M. Sato, Phys. Rev. B 105 , 094306 (2022)。[8] R. Okamoto、N. Kawakami 和 H. Obuse(准备中)。
超导量子比特的非厄米动力学中的量子跳跃
耗散在自然界中普遍存在;例如原子核的放射性衰变和吸收介质中的波传播,耗散是这些系统与不同环境自由度耦合的结果。这些耗散系统可以用有效非厄米汉密尔顿量进行现象学描述,其中引入非厄米项来解释耗散。非厄米性导致复杂的能谱,其虚部量化系统中粒子或能量的损失。非厄米汉密尔顿量的简并性称为异常点 (EP),其中特征值和相关的特征态合并 [1,2]。 EP的存在已在许多经典系统中得到证明[3-11],并应用于激光模式管理[12-14]、增强传感[15-20]和拓扑模式传输[21-24]。
任意子系统中多体非厄米趋肤效应的动态抑制
非厄米趋肤效应 (NHSE) 是非平衡系统中一种令人着迷的现象,其中本征态大量局限于系统边界,将系统中加载的(准)粒子单向泵送到边界。最近,它与多体效应的相互作用得到了广泛的探索,并且已经证明粒子间排斥或费米简并压力会限制 NHSE 在其本征解和动力学中引起的边界积累。然而,在这项工作中,我们发现任意子统计数据可以更深远地影响 NHSE 动力学,抑制甚至逆转状态动力学朝着 NHSE 的局部方向。当涉及更多粒子时,这种现象更加明显。该系统中量子信息的传播显示出更加奇特的现象,其中 NHSE 仅影响热集合的信息动力学,而不会影响单个初始状态。我们的研究结果为探索由 NHSE 与任意子统计之间的相互作用引起的新型非厄米现象开辟了一条新途径,并有可能在超冷原子量子模拟器和量子计算机中得到证明。
包括糯米在内的 133 种其他商品
收集。 7 关于样品的提交 (1) 提交项目 食品采购申请书/投标书上带有圆圈标记的项目为必须提交样品的项目。 (2) 样品提交日期:2020 年 6 月 18 日星期二 10:00 之前提交给立川驻军食品食品组(注明数量、产品名称和供应商名称) 8. 投标无效 (1) 不具备第 2 款所述参加竞争性招标所需资格的人投标。 (2) 投标金额、投标人姓名和印章难以识别。 (3) 通过电报、电话、或传真。 (4) 未在指定时间到达的投标人(到达确认由发送人负责) (5) 对被拒绝样品的产品或未提交样品的产品进行投标 (6) 如果投标人等的承诺不真实,或者出现违反承诺的情况,则投标人等提交的投标文件等无效。