XiaoMi-AI文件搜索系统
World File Search System分子状态的信息论描述和反应物之间的电子通信
Fisher [ 1 ] 和 Shannon [ 3 ] 的信息论 (IT) [ 1 – 8 ] 已成功应用于分子电子结构的熵解释 [ 9 – 11 ]。人们研究了一些信息原理 [ 9 – 16 ],并对分子中原子的分子电子密度片段 (AIM) 进行了研究 [ 12 , 16 – 20 ],为 Hirshfeld 的直观股东分裂提供了 IT 基础 [ 21 ]。人们从分子中的电子通信中提取了熵键多重性的模式[9-11,22-32],探索了分子中的信息分布[9-11,33,34],并将非加性 Fisher (梯度) 信息[1,2,9-11,35,36]与密度泛函理论 (DFT) [40-45] 的电子局域化函数 (ELF) [37-39] 联系起来。该分析制定了用于定位化学键的逆梯度 (CG) 探针[9-11,46],而利用分子信息系统中的“级联”传播的化学键轨道通信理论 (OCT) 已确定了 AIM 之间的桥相互作用[11,47-52],通过中间轨道实现。分子系统的量子电子态及其动力学由薛定谔方程 (SE) 确定。这些 (复) 波函数由其模量和相位分量指定,它们产生系统电子的概率和电流分布。这些物理属性分别反映了“存在”和“成为”的互补经典 (静态) 和非经典 (动态) 结构,它们都对状态总熵和信息内容有所贡献。研究它们的连续性关系以建立这些属性的净产量并确定其来源的起源是有意义的。在量子力学 (QM) 中,波函数相位或其梯度决定了概率密度的有效速度,从而产生了非经典信息和熵补充
生物能量学
4-下列哪一项关于生化反应中自由能变化(ΔG)的陈述是正确的?A. 如果ΔG为负,则反应会自发进行,同时损失自由能。B. 在放能反应中,ΔG为正。C. 当反应物浓度为 1.0 mol/L 且 pH 值为 7.0 时,标准自由能变化表示为ΔG0 D. 在吸能反应中,ΔG为负。5-如果反应的 ΔG 为零:A. 反应实际上会完成并且基本上是不可逆的。B. 该反应是吸能的。C. 该反应是放能的。D. 只有在可以获得自由能的情况下,反应才会进行。E. 系统处于平衡状态,没有发生净变化。 6-ΔG0' 定义为以下情况下的标准自由能电荷:A. 反应物的浓度为 1.0 mol/LB 反应物的浓度为 1.0 mol/L,pH 值为 7.0。C. 反应物的浓度为 1.0 mmol/L,pH 值为 7.0。D. 反应物的浓度为 1.0 μmol/LE 反应物的浓度为 1.0 mol/L,pH 值为 7.4。7-如果 ΔG ⁰ = -10 kcal/mole,则意味着:A) 该反应是非自发的 B) 该反应可与吸能反应相结合 C) 该反应速度较慢 D) 该反应可能是水解反应 E) B+D
手性阳离子指导的对映选择性过渡金属催化
在手性阳离子催化中,催化剂与阴离子中间体配对,通常是由无机碱基的反应物质子抽象引起的它形成的。例如,诸如烷基化,迈克尔添加,藻反应和曼尼奇反应等反应已经融合了中间体,并且可以使用手性阳离子相转移的细胞来促进中间体。1 B其他阴离子(例如氰化物和uoride)也可以使用这种方法分别激活以进行氰化和uorination。然而,涉及中性电子状态的反应物或对无机碱基的反应物不能使用手性阳离子催化剂进行催化。因此,为了扩大手性阳离子催化的范围,人们热切期望制定避免这种弱点的策略。为了激活与甘氨酸schi b碱添加的烯丙基醋酸盐,锣3 a和takemoto 3 b,c在
火星 - 曲面 - 生成 - 挑战 -
燃料电池经常提出,但是它们不能很好地构成质量,因为它们要么需要降落的反应物质量,要么需要更多的能量和生产量才能使反应物与燃料电池提供的原位。生物关系(依靠微生物将有机原料直接转化为热量或其他商品,例如甲烷,然后可以用来产生能力),也已被提议作为发电技术选择。但是,微生物的引入可能会因行星保护的限制而变得复杂。此外,如果由于存在高氯酸盐或其他化学物质及其副产品,可能需要采取原料/生物量补充涉及火星土壤,则可能需要采取其他安全/加工措施。
10年级科学C3定量化学(PDF)
如果质量增加 - >一种反应物可以是气体,例如金属与空气中的氧气反应。如果质量减少 - >其中一种可能是气体,例如释放氢气的气泡。
牛津AQA IGCSE化学修订说明
反应物的质量始终等于产物的质量,但是在反应过程中,质量似乎已经丢失或获得。如果在反应过程中释放出气体,则质量似乎已经丢失。如果物质与气体反应,则似乎已经获得了质量。您的笔记
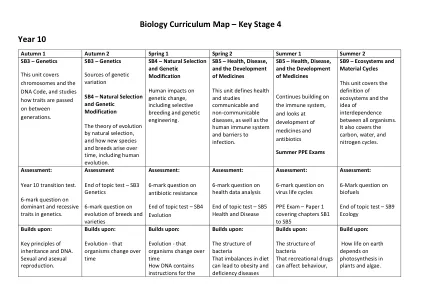
生物学课程图 – 关键阶段 4 10 年级
扩散 不同的动物细胞及其适应性 介绍: 更多关于光合作用以及不同因素如何影响其速率的知识 不同因素如何影响植物对水的吸收速率 光合作用的反应物和产物如何运输 更专业的细胞:栅栏细胞、根毛细胞、木质部细胞和韧皮部