XiaoMi-AI文件搜索系统
World File Search SystemQuantum-Safe密码学中的加密方法
简介量子计算有助于重新定义功能,将量子的原理作为叠加原理和纠缠的速度比经典系统更快。t在众多D材料科学,药物发现和ARTIF中具有巨大的潜力,但它也引入了基本密码系统。Classical public-ke such as RSA, ECC, and DSA, rely on mathe like integer factorization and discrete logar computationally difficult for classical com Quantum algorithms, such as Shor's and Gr these problems efficiently, making these sy In response to this emerging threat, the quantum-safe cryptography has become es safe cryptography aims to develop cryptogra can withstand classical and quantum comp Efforts like the National Institute of标准(NIST)量子后密码学单位在评估和耐药算法方面至关重要。
自然工程与DNA纳米技术简介
在本课程的第一单元中,我们将探索水滴在各种表面上的干燥机制。然后,我们将研究含有固体颗粒的液滴的干燥模式。进入第二单元,我们将研究干燥水滴溶液在组织工程、微电子制造、印刷质量控制和医学诊断等领域的实际应用。第三单元将重点介绍水滴在表面上的运动,特别强调超疏水表面,这导致了自清洁材料的发展。在第四单元中,我们将深入研究扩散现象,包括菲克第一和第二扩散定律,以及膜科学和工程的应用。还将研究扩散分子对聚合物链的塑化与聚合物的粘弹性行为及其工程应用的关系。第五单元将介绍时间叠加原理及其应用,以及吸附机制及其与碳捕获和全球变暖效应等问题的关系。在第六个也是最后一个单元中,我们将重点介绍 DNA 纳米技术,探索随机
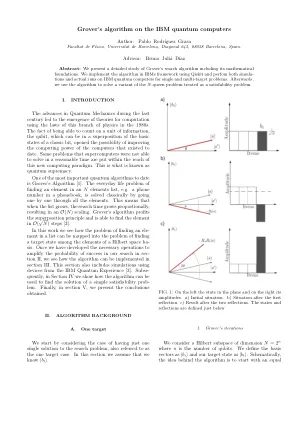
Grover的算法IBM量子计算机
上个世纪的量子力学进步导致了使用该物理学分支在1980年代的定律中出现计算理论。能够依靠一个信息单位的事实,即可以在经典位的基本状态叠加的量子,这打开了提高迄今为止现有计算机的计算能力的可能性。超级计算机无法在合理时间内无法解决的一些问题被放置在此新计算范式的范围内。这就是所谓的量子至上。迄今为止最重要的量子算法之一是Grover的算法[1]。在n个元素列表中找到元素的日常生活问题,例如电话簿中的一个电话号码是通过一个元素一个一个一个一个一个一个元素的一个人来解决的。这意味着当列表增长时,搜索时间会成比例地增长,从而导致O(n)缩放。Grover的算法可拟合叠加原理,并能够在O中找到元素(√
应力强度因子叠加在考虑裂纹闭合的残余应力场中的应用
应力强度因子 (SIF) 范围与疲劳裂纹扩展之间的相关性是应用于轻型结构的故障安全设计方法的有力工具。关键作用是精确计算疲劳载荷循环的 SIF。先进的材料加工可以塑造残余应力,使 SIF 计算成为一项具有挑战性的任务。虽然 SIF 叠加成功地解决了拉伸残余应力的考虑问题,但压缩残余应力的处理仍需澄清。这项工作展示了 SIF 叠加原理在包含高压缩残余应力的区域中的应用,这些区域会导致裂纹闭合效应。裂纹闭合取决于残余应力和施加应力的组合载荷,在本研究中被解释为裂纹几何形状的变化。因此,源(即施加或残余应力)与其结果(即相应的 SIF)之间的关系取决于源(即组合载荷)的相互作用。由于这种相互作用,残余应力引起的疲劳行为变化不能仅与残余或施加的 SIF 相关联。这项工作提出了应用 SIF 和残余 SIF 的两种替代定义,从而允许残余 SIF 或应用 SIF 与疲劳行为变化之间建立明确的相关性。
聚合物和聚合物复合材料的环境老化建模——耐久性预测方法
摘要:聚合物和聚合物复合材料受到环境老化的负面影响,从而缩短了它们的使用寿命。材料与环境相互作用的不确定性损害了它们的优异强度和刚度。新型复合材料和结构的验证通常涉及冗长而昂贵的测试程序。因此,建模是一种经济实惠的替代方案,可以部分替代大量测试,从而降低验证成本。耐久性预测模型通常会受到多功能性和验证所需的最少实验工作量之间相互冲突的要求。基于对复合材料宏观性能的物理观察,工程和现象学模型提供了复杂机械模型的可管理表示。本综述系统地概述了用于预测聚合物和聚合物复合材料长期机械性能的最新模型和加速测试方法。概述了在环境因素的单一或耦合影响下预测各种聚合物和聚合物复合材料的静态、蠕变和疲劳寿命的加速测试方法。通过降解率模型、叠加原理和参数化技术预测使用寿命。本综述是作者关于聚合物复合材料环境老化建模工作的延续:综述的第一部分涵盖了环境降解的多尺度和模块化建模方法。本研究的重点是工程机械性能建模。
FastField:用于有效近似深部脑刺激电场的开源工具箱
深部脑刺激 (DBS) 是一种通过电调节神经组织来缓解某些脑部疾病症状的外科疗法。预测电场和激活组织体积的计算模型是有效参数调整和网络分析的关键。目前,我们缺乏支持复杂电极几何形状和刺激设置的高效灵活软件实现。现有工具要么太慢(例如有限元法 - FEM),要么太简单,对基本用例的适用性有限。本文介绍了 FastField,一个用于 DBS 电场和 VTA 近似的高效开源工具箱。它根据叠加原理计算可扩展的电场近似,并根据脉冲宽度和轴突直径计算 VTA 激活模型。在基准测试和案例研究中,FastField 的求解时间约为 0.2 秒,比使用 FEM 快 ∼ 1000 倍。此外,它几乎与使用 FEM 一样准确:平均 Dice 重叠度为 92%,这大约是临床数据中发现的典型噪声水平。因此,FastField 有潜力促进有效的优化研究并支持临床应用。
从多指双极晶体管中的测量数据中提取真实的手指温度
摘要 - 在此简介中,我们提出了一种逐步策略,以准确估计基于硅的多纤维双极晶体管结构中的纤维温度,从常规的调查中。首先,我们在给定的环境温度下提取几乎零动力的自加热电阻(r TH,II(t a))和热耦合因子(C IJ(t a))。现在,通过将叠加原理应用于几乎零功率的这些变量上,其中保留了热扩散方程的线性,我们估计有效的热电阻(r th,i(t a))和相应的修订后的效率温度t i(t a)。最后,Kirchhoff在T I(t a)上的trans形得出每个纤维处的真实温度(t i(t a,p d))。所提出的提取技术自动包括晶体管结构中存在的后端金属层和不同类型的沟渠的影响。该技术是针对具有不同发射极尺寸的双极晶体管的3D TCAD模拟结果验证的,然后应用于从stmicroelectronics B5T技术中从最先进的多纤维sige HBT获得的实际测量数据。可以观察到,原始测量数据在40 mW左右的叠加量低估了真正的纤维温度约10%。
DSC 5:量子力学简介
DSC 5:量子力学简介单元3教学大纲:简要讨论古典物理学解释黑体辐射,光电效应,康普顿效应,原子的稳定性和原子光谱。康普顿散射:Compton Shift的表达(带推导)。物质波:物质波,电子显微镜,波数据包的颗粒的波浪描述,组和相位速度的波浪描述,物质波的实验证据:Davisson-Germer实验,G.P Thomson的实验及其意义。海森伯格不确定性原理:海森堡动量与位置,能量和时间,角动量和角位置之间关系的基本证明,伽玛射线显微镜思维实验的不确定性原理的说明。不确定性关系的后果:电子在单个缝隙中的衍射,核中电子的不存在。对光子和电子的两缝实验。线性叠加原理因此。_______________________________________________________________________________________ Brief discussion on failure of classical physics to explain black body radiation, Photoelectric effect, Compton effect, stability of atoms and spectra of atoms.古典力学无法解释以下现象:1)它在原子维度的区域中不存在,即无法解释
量子技术中的量子最佳控制。欧洲研究现状,愿景和目标的战略报告
1引言量子最佳控制理论(QOCT)是指设计和实施外部电磁场的形状的一组方法,这些方法以最佳方式以原子或分子量表操纵量子型的过程[246]。它以控制理论为基础,以更笼统的术语为基础,这些术语以应用数学,工程和物理学之间的接口发展,并涉及对实现特定任务的动态过程的操纵。主要目标是使正在研究的动力系统可以最佳地运行并达到其物理限制,同时满足手头设备施加的约束。量子过程也不例外,但必须对控制理论的某些方面进行调整以考虑量子世界的特殊性。在过去的几年中,Qoct已成为新兴量子技术的组成部分[6],这证明了以下事实:控制将科学知识转化为技术[246]:如果叠加原理是量子力学的核心特征,则量子力学的核心特征,量子控制是量子控制的主要原理。量子技术需要相对良好的且特征良好的量子系统。与使用QOCT(例如化学反应动力学)相比,这一特征使它们成为Qoct的理想测试。相反,Qoct已经成熟到如今在实验中很容易使用的阶段。Qoct的下一个挑战将是成为
量子计算不同量子比特设计的比较
„ 引言 在过去十年中,量子计算一直是一个不断发展的领域。与依靠比特将信息表示为 0 或 1 的传统计算机不同,量子计算机使用量子比特或量子位,由于叠加原理,量子比特可以同时存在于多种状态中。预计量子计算机解决特定问题的速度将比传统计算机快得多。这些问题包括复杂的量子模拟 1 和特定的优化任务。2 量子计算还可用于加密。3,4 量子计算应用是一个不断发展的领域,随着量子计算机计算能力的增长,它们也在不断发展。量子计算机的这些潜在应用引起了人们对该领域的极大关注,人们对这些计算机的设计和改进进行了广泛的研究。量子位是量子计算机中最小的计算单元,其属性决定了计算所需的设计。设计量子位的第一步是定义量子计算机需要满足的标准,才能被视为实用的计算机设计。理论物理学家 David P. DiVincenzo 在 21 世纪提出了这些特性。5 DiVincenzo 提出了量子计算的五个必要条件和量子通信的两个必要条件。DiVincenzo 的量子计算标准如下: