XiaoMi-AI文件搜索系统
World File Search System1. SALC 和 SAMO 的生成
可约表示 (RR),Γ red ,是通过对位于每个原子位置上的 p 个原子轨道应用点群的对称运算而获得的。在对称运算后留在原子位置上的原子轨道在 Γ red 矩阵的对角线上贡献 +1,而在对称运算后保留其位置但改变相位的原子轨道在 Γ red 矩阵的对角线上贡献 -1。在对称运算后与另一个原子轨道交换位置的原子轨道在 Γ red 矩阵的对角线上贡献 0。使用以下公式可以得到 Γ red 就群的不可约表示 (iRR) 而言的以下约化:
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道
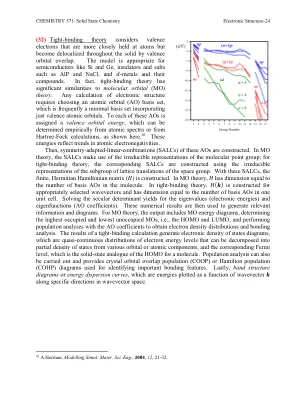
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道重叠进行了离域。该模型适用于SI和GE等半导体,ALP和NACL等绝缘体和盐,以及𝑑金属及其化合物。实际上,紧密结合理论与分子轨道(MO)理论具有显着相似之处。电子结构的任何计算都需要选择原子轨道(AO)基集,该集通常是最小的基础集,仅包含价原子轨道。对这些AOS中的每一个都分配了价值轨道能,可以从原子光谱或Hartree-fock计算中进行经验确定,如下所示。10这些能量反映了原子电负性的趋势。然后,构建了这些AOS的对称适应性线性组合(SALC)。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。 使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。 在MO理论中,𝐻具有等于分子中基本AO的数量。 在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。 求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。在MO理论中,𝐻具有等于分子中基本AO的数量。在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。这些数值结果然后用于生成相关信息和图表。对于MO理论,输出包括MO能量图,确定最高占用和最低的无置置的MOS,即HOMO和LUMO,以及使用AO系数进行电子密度分布和键合分析的人群分析。紧密结合计算的结果产生了状态图的电子密度,这是电子能级的准连续分布,可以分解为来自各种轨道或原子成分的态密度,以及相应的FERMI水平,这是Homo的固态类似物的固态类似物。种群分析也可以进行,并提供用于识别重要键合特征的晶体轨道重叠种群(COOP)或汉密尔顿人群(COHP)图。最后,带结构图或能量分散曲线,这些曲线是沿波向量空间中特定方向的波形绘制的能量。
量子系统的运动分解
经典物理学(如汉密尔顿动力学)和量子物理学(如幺正动力学)的标准描述都描述了封闭系统。它们的形式主义排除了描述与周围环境交换能量的系统的可能性。在经典物理学中,这个问题由波特-汉密尔顿理论解决,该理论允许描述开放系统及其相互作用。在量子力学中,不存在这种全面的开放系统理论。量子系统的组合是由张量积构造定义的,因此量子系统的组合和分解要困难得多。在本文中,我们利用有限维量子系统的任何张量积组合都可以重写为直接和分解这一事实,成功地解决了该问题的运动学部分。通过不失一般性地仅考虑其希尔伯特空间是 SU(2) 的可约或不可约表示的基本量子系统,可以得到唯一的这种直接和分解。现在可以根据这个结果建立以量子端口哈密顿方式分解的量子系统的动力学描述,并进行简要介绍。
dirac Bispinors和旋转1/2状态
摘要。在本文中,我们研究了由洛伦兹提升引起的单个粒子纠缠。我们将粒子描述为自由狄拉克方程的解决方案,一种狄拉克·比斯皮诺(Dirac Bispinor),并将诱导的动量旋转纠缠与在相对论旋转1/2状态的广泛考虑的框架中获得的结果进行了比较。两种方法的自旋线性熵在超级主义极限中一致。我们还验证了双旋格纠缠与双旋转病例的旋转熵之间的不同,表明涉及Dirac Bispinor状态的自由度:动量,自旋,自旋和本质平等的真正多部分纠缠。Dirac Bispinors属于完整Lorentz群体的不可约表示的事实(也包括均等作为对称性),是这种非平凡结构的最终原因。
具有非阿贝尔对称性的开放量子系统的稳态简并性
摘要 我们研究了具有多个非阿贝尔强对称性的开放量子系统的零空间退化。通过将这些对称性的希尔伯特空间表示分解为涉及多个交换不变子空间的直接和的不可约表示,我们推导出稳态退化的严格下限。我们将这些结果应用于开放量子多体系统,并给出了三个说明性示例:全连通量子网络、XXX Heisenberg 模型和 Hubbard 模型。我们发现,在 SU(2) 对称情况下,导出的边界在系统尺寸上至少以立方级缩放,通常是饱和的。此外,我们的工作为具有非阿贝尔对称性的 Liouvillian 的系统块分解提供了一种理论,从而降低了对这些对象进行对角化所涉及的计算难度,并将自然的物理结构暴露给稳定状态——我们在示例中观察到了这一点。
具有非阿贝尔对称性的开放量子系统的稳态简并性
摘要 我们研究了具有多个非阿贝尔强对称性的开放量子系统的零空间退化。通过将这些对称性的希尔伯特空间表示分解为涉及多个交换不变子空间的直接和的不可约表示,我们推导出稳态退化的严格下限。我们将这些结果应用于开放量子多体系统,并给出了三个说明性示例:全连通量子网络、XXX Heisenberg 模型和 Hubbard 模型。我们发现,在 SU(2) 对称情况下,导出的边界在系统尺寸上至少以立方级缩放,通常是饱和的。此外,我们的工作为具有非阿贝尔对称性的 Liouvillian 的系统块分解提供了一种理论,从而降低了对这些对象进行对角化所涉及的计算难度,并将自然的物理结构暴露给稳定状态——我们在示例中观察到了这一点。
第 3 章 自旋的基本量子统计力学...
其中 ϵ abc 是完全反对称张量,ϵ xyz = 1。该代数被称为旋转(即角动量分量)生成代数。这里,旋转不是在自旋的位置,而是在其“方向”上(加引号是因为当然不可能测量量子自旋的所有三个分量)。量子自旋的希尔伯特空间通过选择自旋算子的表示来定义。李代数的表示是一组满足对易关系的三个矩阵,对于 su (2),由 (3.1) 给出。不可约表示是一组矩阵,使得没有一个酉变换 US a U † 能使这三个矩阵块对角化。根据李代数理论,已知对于 su (2),每个整数 n 恰好有一组(最多酉变换)不可约 n × n 矩阵。出于很快就会明白的原因,对于所有整数和半整数 s ,习惯上都写为 n = 2 s + 1 。指标 s 通常被称为粒子的“自旋”,这有点令人困惑。因此,空间中固定点处的单个自旋为 s 的量子粒子具有希尔伯特空间 C 2 s +1 ,因此矩阵 S a 均为 (2 s + 1) × (2 s + 1)。正交基由任何一个矩阵的特征态给出。哪一个并不重要;任何选择的此类基都可以“旋转”(在自旋空间中!)为任何其他基。对于 s = 0,矩阵都由数字零组成;毫不奇怪,这被称为平凡表示。对于 s = 1 / 2,它变得有趣;S a = σ a ℏ / 2,其中 σ a 为
对称保护的量子计算
我们考虑一种使用量子比特的量子计算模型,其中可以测量给定的一对量子态是处于单重态(总自旋为 0)还是三重态(总自旋为 1)。其物理动机是,只要哈密顿量中的所有项都是 SU (2) 不变的,我们就可以以一种不会泄露其他信息的方式进行这些测量。我们推测这个模型等价于 BQP。为了实现这一目标,我们证明了:(1)如果补充单量子比特 X 和 Z 门,该模型能够以多对数开销进行通用量子计算。(2)在没有任何额外门的情况下,它至少与 Jordan 的弱“置换量子计算”模型一样强大 [ 14 , 18 ]。(3)通过后选择,该模型等价于 PostBQP。不完美的物理门是构建可扩展量子计算机的主要挑战。克服这一挑战的一种可能方法是使用纠错码从低保真度物理门构建高保真度逻辑门 [10]。另一种方法是使用拓扑有序状态来存储和操纵量子信息,直接获得良好的逻辑门 [17]。在这里,我们提出了第三种方法,通过物理哈密顿量的对称性保护操作。特别地,我们考虑在量子自旋中编码的量子位,并且我们假设哈密顿量和任何噪声项都遵循同时作用于所有量子位的 SU (2) 对称性。我们需要快速介绍一下 SU (2) 的表示理论。SU (2) 的不可约表示由一个量 S ∈{0, 1 / 2, 1, 3 / 2, ... } 来索引,称为自旋。自旋 S 的表示维数为 2 S + 1 。自旋 1 / 2 的表示维数为
量子自旋系统简介
1. 简介 3 2. 量子自旋系统 3 2.1. 自旋和量子数 3 2.2. 可观测量 4 2.3. 状态 4 2.4. 狄拉克符号 5 2.5. 有限量子自旋系统 7 3. 附录:C ∗ -代数 13 3.1. C ∗ -代数 13 3.2. C ∗ -代数中的谱理论 14 3.3. 正元素 16 3.4. 表示 17 3.5. 状态 18 4. 有限和无限量子自旋系统的一般框架 21 4.1. 有限系统的动力学 21 4.2. 无限系统 24 5. Lieb-Robinson 界限 25 5.1.动力学的存在 30 6. 基态和平衡态 32 6.1. 基态 32 6.2. 热平衡、自由能和吉布斯态的变分原理 33 6.3. Kubo-Martin-Schwinger 条件 35 6.4. 能量-熵平衡不等式 36 7. 无限系统和 GNS 表示 40 7.1. GNS 构造 40 7.2. 无限系统的基态和平衡态 43 8. 对称性、激发谱和相关性 45 8.1. Goldstone 定理 46 8.2. 指数聚类定理 51 9. 附录:李群和李代数 56 9.1.李群和李代数的表示 57 9.2. SU(2) 的不可约表示 60 9.3. 表示的张量积 62 10. 四个例子 64 10.1. 例 1:各向同性的海森堡模型 64 10.2. 例 2:XXZ 模型 66 10.3. 例 3:AKLT 模型 66 10.4. 例 4:Toric Code 模型 67 11. 无失稳模型 68 11.1. AKLT 链 69 11.2. 具有唯一矩阵积基态的无失稳自旋链 77 11.3. 平移不变矩阵积态的一些性质 78 11.4. 交换性质。 82
魔角石墨烯中多体波函数的量子纹理
方法样品制备使用“撕扯和堆叠”方法制造器件。用聚乙烯醇(PVA)拾取石墨烯和hBN。然后,将异质结构翻转到由甲基丙烯酸甲酯共聚物(Elvacite 2550/透明胶带/Sylgard 184)组成的中间结构上,并转移到具有 Ti/Au 电极的预先图案化的 SiO 2/Si 芯片上。将残留聚合物溶解在N-甲基-2-吡咯烷酮、二氯甲烷、水、丙酮和异丙醇中。我们进一步使用AFM尖端清洁和高温形成气体退火程序清洁样品表面。最后,将器件在170°C的超高真空中退火12小时,并在400°C下退火2小时,然后将其转移到STM中。 STM 测量 STM/STS 测量是在自制的稀释制冷机 STM 上进行的,其钨尖端在 Cu(111) 表面上制备。MATBG 的载流子密度由施加到简并掺杂 Si 的栅极电压 V g 和通过 Au/Ti 电极施加到 MATBG 的样品电压 V s 控制。dI/dV 是通过锁定检测由添加到 V s 的交流调制 V rms 引起的交流隧道电流来测量的。测量是在样品偏置电压 V s 接近零的情况下进行的,以避免由于 K 点或 M 点声子 43 引起的非弹性隧穿。序参数分解有关此过程的完整详细信息和说明,我们请读者参阅 SI。简而言之,大型低偏置 STM 图像被分割成较小的 0.25 - 1 nm 2 子区域。每个子区域都相对于每个子区域的中心进行傅里叶变换。我们对 FFT 峰值应用位置相关的相位因子,以强制跨子区域保持一致的原点。在 IVC 波矢处获得的每个局部 FFT 的三个独立复值分解为三个复 IVC 序参数(“IVC 键”、“IVC 位点 A”和“IVC 位点 B”),它们对应于 C 3 点群的三个不可约表示 {(1, 1, 1)、(1, ω, ω 2) 和 (1, ω 2 , ω),其中 ω ≡ e 2πi/3 }。根据构造,如果 LDOS 是莫尔周期的,则这些序参数也是莫尔周期的。参考文献:1. Cao, Y. 等人。魔角石墨烯半填充时相关绝缘体的行为