XiaoMi-AI文件搜索系统
World File Search SystemOPSA:带有TEE的有效且可验证的一通安全聚合用于联合学习
摘要 - 在联合学习,安全的聚合(SA)促成(S&P'23)和Lerna(Asiacrypt'23)等诸如恶意模型中已实现了有效的多轮SA。但是,他们的每一轮聚合需要至少三个客户服务器往返通信,并且缺乏对聚合结果验证的支持。可验证的SA方案,例如Versa(TDSC'21)和Eltaras等。(TIFS'23),根据服务器不与任何用户相关的安全性假设提供可验证的聚合结果。尽管如此,这些方案会产生高沟通成本,并且缺乏对有效的多轮聚合的支持。完全在SEAR中(TDSC'22)中完全在受信任的执行环境(TEE)中执行SA,可以保证隐私和可验证的聚合。但是,T恤中的有限物理内存带来了重要的计算瓶颈,尤其是在汇总大型模型或处理众多客户时。在这项工作中,我们介绍了OPSA,这是一种基于TEE的多轮安全聚合框架,以实现有效的通信,简化的计算和可验证的聚合。OPSA采用了一种新的策略,可以在TEE中揭示共享键,并实例化两种类型的掩盖方案。 此外,结果验证模块设计为与在OPSA框架下实例化的任何类型的SA协议兼容,并且安全性假设较弱。 与最先进的方案相比,OPSA在多轮聚集中达到了2个〜10×速度,同时也支持结果验证。OPSA采用了一种新的策略,可以在TEE中揭示共享键,并实例化两种类型的掩盖方案。此外,结果验证模块设计为与在OPSA框架下实例化的任何类型的SA协议兼容,并且安全性假设较弱。与最先进的方案相比,OPSA在多轮聚集中达到了2个〜10×速度,同时也支持结果验证。OPSA对具有高网络延迟和大规模模型聚合的方案更友好。
SD-BLS:隐私保存选择性披露可验证的凭据,并具有不可链接阈值吊销
隐私违反撤销清单,我们认为匿名撤销是condicio condicio siin qua non to vasee,在数字身份和证书中是足够的隐私水平。在Eudi-arf或W3C-VC和BBS+中没有设计隐私的吊销系统。如果选择撤销战略的选择将向开发商开放,则可能会发生重大隐私违规的风险,例如,采用公共公共设备清单[7]。证书状态列表(CRL)的偏瘫使用介绍了主要与隐私相关的问题[8],因为有关持有人的敏感信息从列表中泄漏。如果凭证可能是短暂的(通常不太重要的凭据),但不适用于数字识别文件,例如ID,驾驶执照,护照和社会保险号,而这些凭据更长或没有到期时间。我们观察到的国家标准的未来计划包括采用“ Bitstring”状态清单[9],这些状态可能会授予隐私权。在SD-BLS中,我们设计了一种隐私的吊销机制,以消除持有人的信息的泄漏,并将撤销的治理委派给了多个撤销发行人的法定人数,这可能与证书发行人不同。
年龄验证系统访问在线内容
在发行过程中,可验证的凭据与使用最终用户的公共密钥创建的DIT(分散标识符)链接,从而有效地使DID获得了可验证的凭据,从而确认了多数年龄。通过使用用于创建DID的公共密钥链接的专用密钥进行的签名,该匿名关联可以保证只有所有者才能提供可验证的凭据。换句话说,该凭据由数字管理秘书处(SGAD)签署,然后由用户再次签署,确保只有用户才能将其呈现给第三方。这可以确保通过公共密钥进行可追溯性,因为在提供凭据时,内容提供商将始终获得相同的公钥。由数字管理总秘书处开发的本文档中提出的解决方案旨在减少用户分析。
Stephen Smalley NSA高级网络安全研究实验室(LACR)
•可验证的,值得信赖的软件和配置报告•保护长期秘密免受泄漏和滥用的保护•即使面对完整的软件折衷,也有弹性
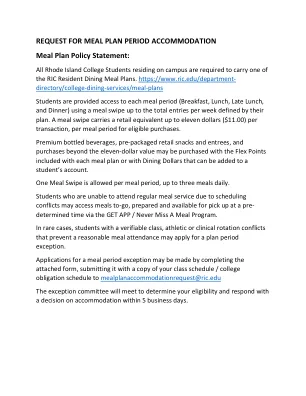
适用于 Apple 的 COVID-19 疫苗接种卡
如果您之前曾扫描二维码、下载文件或联系医疗保健提供者在 iPhone 或 iPod touch 上添加健康记录,则您可以将存储的可验证的 COVID-19 疫苗接种记录添加到 Wallet。
EE382 2010 年春季 - 电气工程
经常被忽视的方面。现实一点来说,应该有办法证明该目标在技术上是可行的。例如,要求可能表明机器人以 1,000,000 英里/小时的速度行驶。它是抽象的、可验证的、明确的——然而,无法实现。
申请膳食计划期间住宿
我承认,我申请膳食计划住宿是因为存在合法且可验证的冲突。我进一步承认,并非所有请求都会得到批准,膳食计划住宿申请委员会将在我提出申请后的 5 个工作日内审核我的申请并做出决定。
讲座 1:量子计算硬件概况和简介
算法我们的具体目标是:(1) 为未来的容错硬件开发新型量子算法,(2) 开发适合更有限计算资源的替代量子计算范式,以及 (3) 扩大量子计算对经典计算机科学的影响。可验证的量子优势我们应对这一挑战的具体目标是:(1) 开发严格可验证的量子优势协议,(2) 细化噪声和误差模型与计算能力之间的联系,以及 (3) 开发 NISQ 计算最有价值的应用之一,即通过量子模拟推动物理科学的发展。扩展基于原子的计算机的具体目标是利用 AMO 研究扩展量子系统挑战的具体目标是利用基于 AMO 的量子技术,包括光学工程的进步,在不断增加的大小和复杂性的量子系统中实现改进的模块化、高保真操作和经典控制,从而推导出扩展量子信息处理器的通用方法。