XiaoMi-AI文件搜索系统
World File Search System量子计算机噪声的时间研究
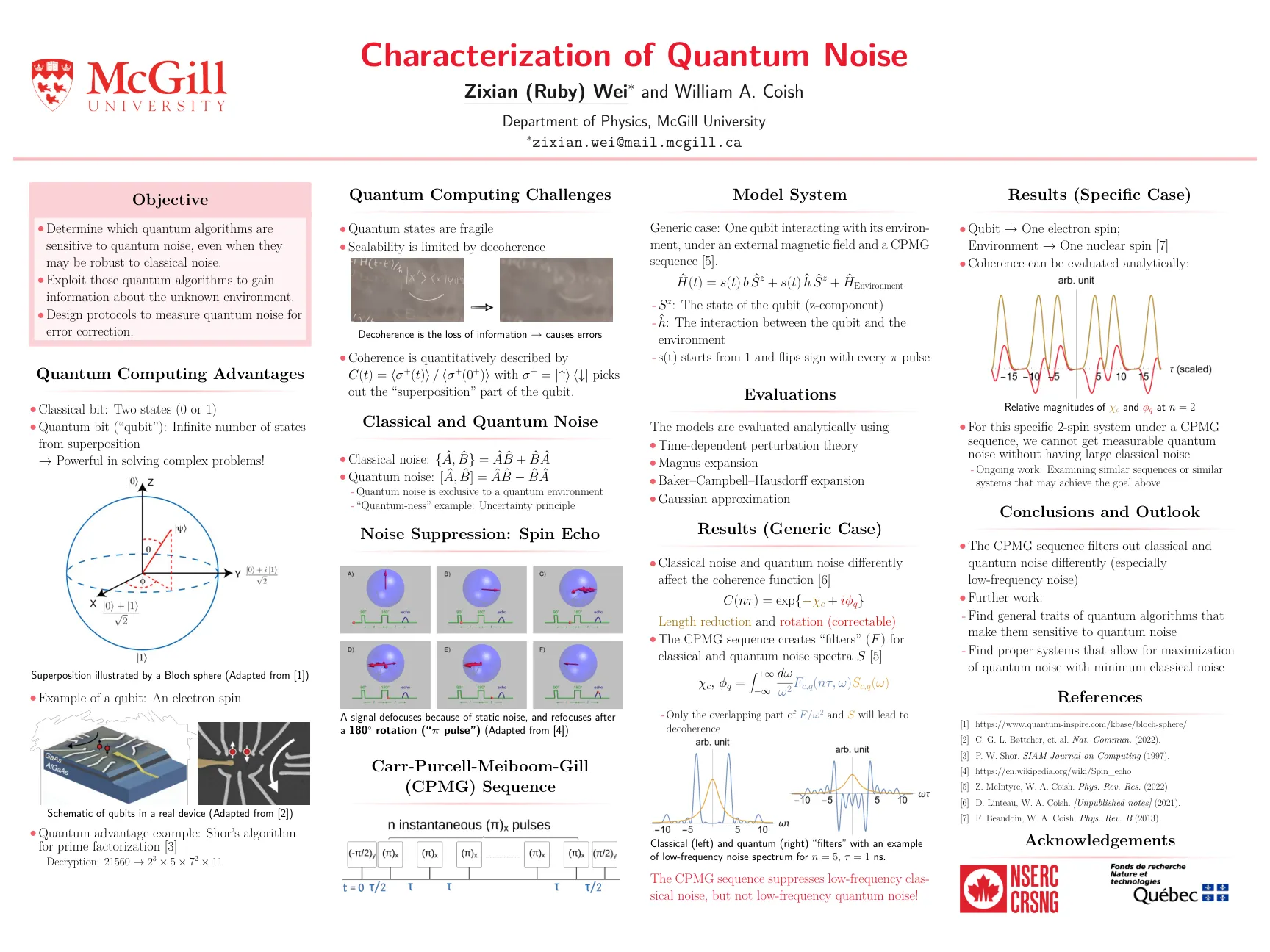
摘要 — 在过去的几年中,量子计算 (QC) 引起了计算机科学家的兴趣,因为它具有量子加速、解决 NP 难题的可能性以及实现更高的计算能力。然而,减轻每个量子设备内部噪声的影响是一个迫在眉睫的挑战。这些变化为研究校准参数对每个量子比特的个体特征的影响提供了新的机会。在本文中,我们基于校准数据和单个设备的特性研究了嘈杂的中型量子 (NISQ) 计算机的时间行为。具体来说,我们收集了过去两年 IBM-Q 机器的校准数据,并将量子误差鲁棒性与 IBM-Q 机器的处理器类型、量子拓扑和量子体积进行比较。索引术语 — 量子计算、量子特性、量子时间研究、量子误差
任意Pauli噪声的错误阈值
[Schumacher '96;舒马赫,尼尔森'96;劳埃德'97; Shor '02; Devetak '05;渡边'12; Cubitt '15]
转录噪声的工程蜂窝交响曲
真核细胞导航混乱的环境,其中随机细胞过程会收敛以产生细胞表型。从混乱中出现,基因表达的精确协调模式支持诸如组织稳态和发育模式等细胞行为。经过细胞的转换后,尽管内部和外部干扰,细胞在长期内保持稳定的身份。细胞种群如何保持稳定性,同时保留足够的可塑性以应对外部提示和侮辱?缓冲和线束反式十字噪声的内源性机制正在成为赋予稳定性和可塑性的调节系统。虽然当前的合成回路主要围绕基因表达的平均水平而设计,但通过研究转录调控而获得的见解表明,刺激转录噪声具有对工程真核细胞和组织的有望。
基于人工智能的晶体管中电荷噪声的变化
nist.gov › publication › get_pdf 基于 AI 的晶体管中电荷噪声的变化... 2瑞士联邦计量局,3003 Bern-Wabern,瑞士。
用于辐射噪声的垂直线阵列... - RTSYS
由于传感器尺寸的原因,阵列尺寸减小到 31 毫米,并且足够轻,长度不到 20 米,一个人就可以轻松操作。内部不锈钢电缆和 Dyneema 编织纺织外电缆提供了高强度和声学噪声保护的完美结合。软件,例如 ©PAMguard、R、Python 和 ©Matlab。
广泛的自动乘车驾驶和对交通噪声的影响
实施高效且可持续的乘车系统需要制定良好的战略和伴随的公共政策。在基于严厉的停止场景中观察到最高的潜力。尽管这种情况在政治上可能不可行,但它显示了可以通过乘车来实现多少流量和降噪的上限。可以通过基于停止的服务设计观察到少量降低噪音,尤其是在居民区。门到门服务甚至可能会增加居民区的噪音。这项研究发表在运输研究部分,可访问开放式:https://doi.org/10.1016/j.trd.2020.102673
面对高噪声的基于纠缠的量子通信的途径
•QKD是量子信息科学的主要应用•实际实现易受噪声•噪声阻碍:1。可实现的关键费率2。传输距离•提高噪声阻力是剩余的关键挑战之一•我们通过将信息编码为𝑑-
基准测试量子计算机和量子噪声的影响
基准测试是如何确定计算系统的性能。令人惊讶的是,即使对于古典计算机来说,这也不是一个简单的过程。必须选择适当的基准和指标来提取有意义的结果。不同的基准测试以不同的方式测试系统,每个单独的指标可能会或可能不是感兴趣的。选择适当的方法很棘手。对于量子计算机来说,情况更加开放,那里的硬件范围更大,建立的指南更少和其他复杂因素。值得注意的是,量子噪声会显着影响性能,并且难以准确建模。在这里,我们从计算机体系结构的角度讨论量子计算机的基准测试,并提供数值模拟,突出了暗示谨慎的挑战。