XiaoMi-AI文件搜索系统
World File Search System复合 - 弗里米昂在半填充和四分之一...
在半完整的最低兰道水平上,Halperin-Lee-Lee读取的复合材料费米斯是一个引人入胜的金属相,它是从电子角度出发的强烈相关的“非弗里米液体”。值得注意的是,实验发现,随着量子井的宽度增加,该状态将过渡到分数量子厅状态,自从三十多年前发现以来,其起源一直是一个重要的难题。我们使用系统的变分框架进行详细且准确的定量计算,以配合复合费米子的配对,这些框架紧密模仿了Bardeen-Cooper-Schrieffer超导性的理论。我们的计算表明,(i)随着量子 - 孔宽度的增加,占量子的最低对称子带的单组分复合材料费米·费米(Fermi Sea)将不稳定的不稳定性进入单组P波 - 复合材料的配对状态; (ii)量子孔宽度 - 电子密度平面中的理论相图与实验非常吻合; (iii)量子井的电荷分布中有足够的不对称性破坏了分数量子霍尔的效应,如实验上所观察到的; (iv)两个组件331状态在能量上比单组分配对状态的好处。在四分之一填充的最低兰道水平的宽量子井中也可以看到分数量子大厅效应的证据;在这里,我们的计算表明复合费米子的F波配对状态。提到了各种实验意义。我们进一步研究了等于一个的填充因子的最低兰道水平的玻色子,并表明复合费米子的P波配对不稳定性是携带单个涡流的玻色子,对于短范围以及库仑的相互作用,与精确的焦点研究相一致。通过实验的复合 - 弗里米式 - 贝尔·索菲夫方法的一般一致性为复合feermion配对的概念提供了支持,这是在均匀施加剂纤维效果下的分数量子响应效应的主要机制。
复合 - 弗里米昂在半填充和四分之一...
在半填充的最低兰道水平上,Halperin-Lee-Lee读的复合材料式费米斯是一个引人入胜的金属相,它是从电子的角度出发的强烈相关的“非Fermi液体”。值得注意的是,实验发现,随着量子井的宽度增加,该状态将过渡到分数量子霍尔状态,自从三十多年前发现以来,其起源一直是一个重要的难题。我们使用系统的变分框架进行详细而准确的定量计算,以配合复合费米子的配对,这些框架紧密模仿了Bardeen-Cooper-Schrieffer超导性的理论。我们的计算表明(i)随着量子 - 孔宽度的增加,占据量子的最低对称子带的单个成分复合材料费米式海洋井口将不稳定置于单一组件p-波配对的复合材料材料状态; (ii)量子孔宽度 - 电子密度平面中的理论相图与实验非常吻合; (iii)量子井的电荷分布中有足够数量的不对称性破坏了分数量子霍尔的效应,如实验性观察到的; (iv)两个组件331状态在能量上比单个组件配对状态的好处。在四分之一填充的最低兰道水平的宽量子井中已经看到了分数量子厅效应的证据;在这里,我们的计算表明复合费米子的F波配对状态。提到了各种实验意义。我们进一步研究了等于一个的填充因子的最低兰道水平的玻色子,并表明复合费米子的p波配对不稳定性,它们是携带单个通量量子的玻色子,对于短范围以及库仑的相互作用,都与精确的直径研究一致。通过实验的复合 - 弗里米亚 - schrieffer方法的一般一致性为偶数量指填充因子的分数量子霍尔效应的机制提供了支持的概念。
汽车悬架系统回顾及四分之一汽车悬架系统介绍
巴巴萨海布·安贝德卡尔大学,奥兰加巴德,印度 摘要:悬架系统可减少由道路和驾驶条件引起的振动的影响。领先的汽车公司已开始在其高端汽车中使用智能悬架。但在行驶过程中,车辆会经历不同程度的动态激励。这种激励可能导致诱发振动或噪音,从而影响车辆的完整性和乘员。车辆系统中一种突出的隔振方法是悬架系统。汽车悬架系统的主要目的是在不影响驾驶操纵特性的情况下提高乘坐舒适度。近年来,执行器、传感器和微电子技术的迅猛发展使得智能悬架系统在汽车工业中更易于实施。这些系统的设计和制造方式能够减少驾驶员和乘客受到的有害垂直加速度的影响。四分之一汽车悬架模型是研究和分析车辆垂直隔离特性动态行为的最佳基准。本文介绍了背景信息和四分之一汽车悬架模型的描述,该模型可用于评估智能悬架系统的性能。关键词:车辆;半主动;悬架;减震器;汽车;自适应;智能;评论;比较
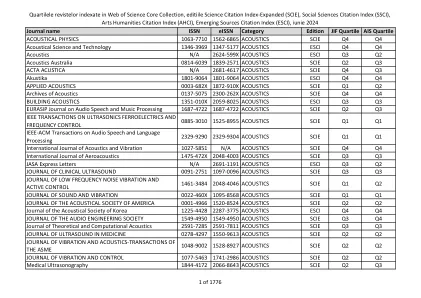
杂志的四分之一索引在科学核心收藏中,科学引文索引扩展(SCIE),社会科学cite Index(SSC
NOISE CONTROL ENGINEERING JOURNAL 0736-2501 0736-2501 ACOUSTICS SCIE Q4 Q4 Noise Mapping N/A 2084-879X ACOUSTICS ESCI Q2 Q3 PHONETICA 0031-8388 1423-0321 ACOUSTICS SCIE Q3 Q1 Romanian Journal of Acoustics and Vibration 1584-7284 1584-7284 ACOUSTICS ESCI Q4 Q4 SHOCK AND VIBRATION 1070-9622 1875-9203 ACOUSTICS SCIE Q3 Q3 SOUND AND VIBRATION 1541-0161 1541-0161 ACOUSTICS ESCI Q4 Q4 SPEECH COMMUNICATION 0167-6393 1872-7182 ACOUSTICS SCIE Q2 Q1 ULTRASCHALL IN DER MEDIZIN 0172-4614 1438-8782 ACOUSTICS SCIE Q1 Q1 ULTRASONIC IMAGING 0161-7346 1096-0910 ACOUSTICS SCIE Q1 Q2 ULTRASONICS 0041-624X 1874-9968 ACOUSTICS SCIE Q1 Q1 ULTRASONICS SONOCHEMISTRY 1350-4177 1873-2828 ACOUSTICS SCIE Q1 Q1 ULTRASOUND IN MEDICINE AND生物学0301-5629 1879-291x声学SCIE SCIE Q2 Q2 Q1超声波在妇产科中超声检查0960-7692 1469-0705 ACOUSTICS SCIE SCIE Q1 Q1波动运动0165-2125 1993-3738农业经济学和政策ESCI Q4 Q4
创新力量_NGSS 和 CCSS_Alignment。
• 1.G3. 将圆形和矩形分成两份和四份,使用二分、四分之一和四分之一等词语描述这些份额,并使用一半、四分之一和四分之一等短语。将整体描述为两份或四份。从这些示例中理解,分解成更相等的份额会产生更小的份额。
创新力量_NGSS 和 CCSS_Alignment。
• 1.G3。将圆形和矩形分成两份和四份相等的份额,使用二分、四分之一和四分之一等词描述份额,并使用一半、四分之一和四分之一等短语。将整体描述为两份或四份。 从这些示例中理解,分解成更相等的份额会产生更小的份额。
指令 038:噪音控制
每四分之一区域的密度——指受影响住宅位于中心的四分之一区域(半径 451 米)。对于土地用途各异或密度混合的四分之一区域,所选密度为所考虑区域的平均值。
Chia-Wei Chen*、Matthias Hartrumpf、Thomas Längle 和 Jürgen Beyerer 通过四分之一波片增强灵敏度的滚动角传感器
摘要:姿态计量(滚转、俯仰和偏航)在许多不同领域发挥着重要作用。与俯仰角和偏航角相比,滚转角被认为是角位移中最难测量的量,因为滚转角的旋转轴与探测光束平行。在本文中,提出了一种灵敏度增强的滚转角传感器。其原理基于传感单元(四分之一波片)的偏振变化。通过 Mueller 矩阵形式分析了偏振模型。斯托克斯参数由斯托克斯偏振计检测。新颖的同轴设计通过固定的四分之一波片提高了灵敏度并降低了光学系统对准的复杂性。所提出的传感器提供了一种简单的装置来测量滚转角,具有 0.006 ∘ 的高灵敏度和 180 ∘ 的长无模糊测量范围。
理事会特别会议 - 2025 年 1 月 25 日 - 议程 - Pdf
从威拉米特子午线以东 40 区第 4 乡镇南侧第 18 区西北区的西北区 [角] 开始,向东延伸一英里半;然后向南延伸一英里四分之一;然后向东延伸一英里四分之一;然后向南延伸一英里四分之一;然后向东延伸一英里半;然后向西延伸一英里四分之一;然后向南延伸一英里;然后向西延伸四分之三英里;然后向北延伸一英里四分之一;然后向西延伸四分之三英里到达威拉米特子午线以东 39 区第 4 乡镇西南区的东南区西北角;然后向北延伸约八分之七英里到凯瑟琳溪;然后以凯瑟琳溪为线向东延伸四分之一英里;然后向北约八分之三英里,到达第 13 区中心、第 4 乡镇南、威拉米特子午线以东第 39 区;然后向东一四分之一英里;然后向北一四分之一英里;然后向东一四分之一英里;然后向北一四分之一英里到达起点。