XiaoMi-AI文件搜索系统
World File Search System图同构
Guardian LVS 中的逻辑门识别
介绍晶体管级电路中常见CMOS门的识别。使用基于规则技术的结构识别算法对于逻辑门识别最有效[1,2,3,4]。这些算法非常快，可以轻松找到静态逻辑门，例如反相器、NAND、NOR、AOI 和 OAI 门。识别后，可以根据逻辑门和剩余的晶体管来比较修改后的网表。表示网表连通性的注释图比晶体管级图小得多，并且可以更好地区分结构。因此，它更有效地解决了电路比较问题，该问题被视为图同构问题 [5] 的一个示例。
格雷戈里罗森塔尔 - 计算机科学
会议论文 Rosenthal, Gregory。“通过一个查询实现高效的量子态合成”。在：2024 年 ACM-SIAM 离散算法研讨会 (SODA) 论文集。2024 年，第 2508-2534 页。doi：10.1137/1.9781611977912。arXiv：2306.01723。Rosenthal, Gregory 和 Henry Yuen。“用于合成量子态和幺正的交互式证明”。在：第 13 届理论计算机科学创新会议 (ITCS 2022)。第 215 卷。2022，112：1-112：4。doi：10.4230/LIPIcs.ITCS.2022.112。 arXiv: 2108.07192 。Rosenthal, Gregory。“近似奇偶校验的 QAC 0 复杂度的界限”。在：第 12 届理论计算机科学创新会议 (ITCS 2021)。第 185 卷。2021 年，32：1-32：20。doi：10.4230/LIPIcs.ITCS.2021.32。arXiv：2008.07470。最佳学生论文奖。Rosenthal, Gregory。“击败平均情况子图同构的树宽”。在：第 14 届参数化和精确计算国际研讨会 (IPEC 2019)。第 148 卷。2019 年，24：1-24：14。 doi：10.4230/LIPIcs.IPEC.2019.24。arXiv：1902.06380。最佳学生论文奖。
使用 HyperGraphs 的 FDG-PET 图像增强抑郁症诊断
摘要 — 本研究探讨了图神经网络 (GNN) 和超图在使用氟脱氧葡萄糖正电子发射断层扫描 (FDG-PET) 图像改善抑郁症诊断的潜力。我们使用核密度估计和动态时间规整从单个静态 FDG-PET 图像构建图形和超图表示。在本地精神病数据集上使用各种 GNN 分类器（包括图卷积网络 (GCN) 和图同构网络 (GIN)）评估这些表示。我们的实验表明，与成对图相比，GNN（尤其是 GCN）在超图上的性能更优越。我们强调了基于超图的表示在捕捉与抑郁症相关的复杂模式方面的整体功效。此外，我们对超图表示的探索为提高诊断准确性提供了有希望的途径，特别是在捕捉复杂的大脑连接模式方面。这项研究为 GNN 有助于使用 FDG-PET 图像更好地诊断精神疾病提供了证据，为个性化治疗策略和跨不同临床环境的诊断进步提供了见解。索引词 — 抑郁症、FDG-PET、KDE、DTW、图、超图、图神经网络、GIN、GCN。
通用顺序搜索问题-Lance Fortnow
在阐明了算法的概念后，证明了许多经典问题的算法不可分辨性（例如，小组元素的认同，流形的同态性，同型二芬太汀方程的溶解性等）。这消除了找到解决方案的实用方法的问题。然而，由于这些算法规定的大量工作，解决其他问题的算法并不能消除它们的类似问题。这是所谓的顺序搜索问题的情况：最小化布尔功能，搜索有限的长度证明，确定图同构以及其他。所有这些问题都是通过列举所有可能性组成的琐碎算法来解决的。但是，这些算法需要指数级的工作时间，而数学家已经形成了信念，即对它们的简单算法是不可能的。已经获得了许多认真的论点以支持其有效性（见[1，2]），但没有人能够证明这一说法。（例如，尚未证明找到数学证据比验证它们需要更多的时间。）但是，如果我们假设存在无法通过简单算法解决的顺序搜索类型的某些（甚至是人为构造的）问题（就计算量而言），则可以证明许多“经典”顺序搜索问题（包括最小化问题，包括最小化问题，证明搜索问题等）也具有此属性。这构成了本文的主要结果。
r22 m. 技术。中央安全与环境部
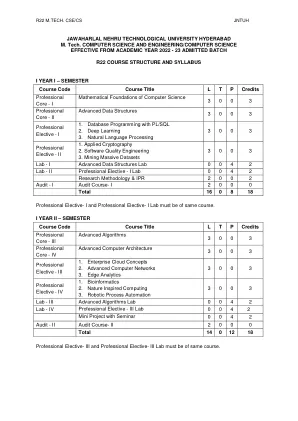
第一单元：基础逻辑与证明：命题逻辑、命题逻辑的应用、命题等价、谓词和量词、嵌套量词、推理规则、证明简介、证明方法与策略。第二单元：基本结构、集合、函数、序列、和、矩阵和关系：集合、函数、序列与和、集合和矩阵关系的基数、关系及其性质、n 元关系及其应用、表示关系、关系的闭包、等价关系、偏序。第三单元：算法、归纳与递归：算法、函数的增长、算法的复杂性。归纳与递归：数学归纳、强归纳与良序、递归定义与结构归纳、递归算法、程序正确性。第四单元：离散概率和高级计数技术：离散概率简介。概率论、贝叶斯定理、期望值和方差。高级计数技术：递归关系、解决线性递归关系、分治算法和递归关系、生成函数、包含-排除、包含-排除的应用。第五单元：图：图和图模型、图术语和特殊类型的图、表示图和图同构、连通性、欧拉和汉密尔顿路径、最短路径问题、平面图、图着色。树：树的简介、树的应用、树的遍历、生成树、最小生成树。教科书：
![arXiv:2004.08681v3 [quant-ph] 2020 年 10 月 21 日](/simg/g:\will\search\icon\source\5\54629a20e2a980c7278538293c6c1948ab71ba1c.webp)
arXiv:2004.08681v3 [quant-ph] 2020 年 10 月 21 日
所有已知例子都表明经典模拟算法与量子绝热量子计算（StoqAQC）之间存在指数分离，这些例子都利用了将绝热动力学限制在有效对称子空间的对称性。对称性产生较大的有效特征值间隙，从而使得绝热计算高效。我们提出了一种经典算法，从任何 k 局部量子汉密尔顿量 H 的有效子空间中进行亚指数采样，而无需先验了解其对称性（或近似对称性）。我们的算法将任何 k 局部汉密尔顿量映射到图 G = ( V, E )，且 | V | = O (poly( n ))，其中 n 是量子比特的数量。鉴于 Babai [ 1 ] 的著名结果，我们利用图同构来研究 G 的自同构，并得出 | V | 中的算法准多项式。用于从 H 的有效子空间本征态中生成样本。我们的结果排除了 StoqAQC 与经典计算之间的指数分离，这种分离是由 k -局部汉密尔顿函数中的隐藏对称性引起的。我们对 H 的图形表示不限于 stoquatic 汉密尔顿函数，并且可以排除非 stoquatic 情况下的相应障碍，或者有助于研究 k -局部汉密尔顿函数的其他属性。
量子统计零知识能力的限制
不可能性证明，如 BQP 在 PP 中的包含 [2, 15]、量子比特承诺的不可能性 [27]，以及预言机和黑盒问题的存在，相对于这些问题，量子计算机的能力有限 [1, 5, 6, 7, 15]。在本文中，我们考虑零知识证明系统的量子变体的潜在优势。零知识证明系统最早由 Goldwasser、Micali 和 Rackooff[20] 于 1985 年定义，此后在复杂性理论和密码学中得到了广泛的研究。本文假设您熟悉零知识证明系统的基础知识。有关零知识的最新调查，请参阅 Goldreich [16]。已经研究了几种零知识概念，但在本文中我们只考虑统计零知识。此外，我们将重点关注诚实验证者统计零知识，这意味着只需一个多项式时间模拟器就可以近似地模拟遵循指定协议的验证者的观点（而不是为了获取知识而故意偏离指定协议的验证者的观点）。在经典情况下，Goldreich、Sahai 和 Vadhan [18] 证明了任何诚实验证者统计零知识证明系统都可以转化为针对任何验证者的统计零知识证明系统。具有统计零知识证明系统的语言类表示为 SZK；已知 SZK 在补集下是封闭的 [32]，SZK ⊆ AM [4, 14]，并且 SZK 具有自然的完全承诺问题 [19, 34]。已知几个有趣的问题（例如图同构和二次剩余）包含在 SZK 中，但不包含在 BPP 中 [17, 20]。有关统计零知识的全面讨论，请参阅 Vadhan [38]。据我们所知，文献中之前没有出现过量子零知识证明系统的正式定义。然而，量子信息是否允许扩展具有零知识证明的问题类别的问题已经被一些研究人员解决了。例如，研究量子比特承诺可能性的动机之一是它对零知识证明系统的适用性。缺乏正式定义的主要原因似乎是当以最直接的方式将零知识的经典定义转换为量子设置时会出现困难。有关这些问题的进一步讨论，请参阅 van de Graaf [21]。本文的目的不是试图解决这些困难，也不是提出一个从密码学角度令人满意的量子零知识定义。相反，我们的目标是研究基于诚实验证者概念的量子零知识简单定义的复杂性理论方面。我们考虑这个定义的主要动机是：