XiaoMi-AI文件搜索系统
World File Search System复数
揭示了农业转型叙事之间的多样性：坦桑尼亚北部基洛姆贝罗山谷的小农户的见解
当前在政策领域中采用的转型话语给予了人们对各种知识，复数道路和政治的关注。关于非洲景观变化和农业转型的叙述是多种多样的。然而，未能认识到主要食品生产者的叙事之间的多样性（卑鄙的农民）在规划和政策过程中限制了实现仅仅实现农业转型的潜力。在本文中，为了了解各种知识，复数途径和农业转型政治的理解，我们介绍了对未来农场的小农主愿景及其在非洲景观中的农业转型叙事及其对快速生态和生计变化的叙述。我们将转型的小农叙述与国家和私营部门蓝图促进的人一起介绍，并认真地反思转型的社会正义。在坦桑尼亚南部农业增长走廊（Sagcot）的北基洛姆贝罗山谷的九个参与式研讨会中，确定了四个主要的转型叙事：（1）土地所有权，（2）（2）农业活动的扩展，（3）多元化，以及（4）供水以供水。小农提出的转型观似乎与国家蓝图政策和计划不相容。这些具有供水的更大，更多样化的农场的视野不一定与该地区的甘蔗种植的扩展兼容，并且尚未在甘蔗膨胀计划中充分认识，从而产生了加剧不公正现象的潜力。尽管“双赢”了转型的叙述以及萨格科特，国家政府和基洛姆贝罗糖业公司促进的甘蔗种植的扩展的外属计划方法，但我们发现，土地所有权和扩张仍然具有挑战性，对现在的小持有人来说仍然具有挑战性，并代表了对未来的关键愿望，以及对灌溉的多样化和获得量的多样性。鉴于缺乏认可，小农倡导在保护其作为公民的利益方面发挥更强大的作用，以与Sagcot私人公共合作伙伴有关。我们表明，非洲农村景观中的参与者需要更大的努力，以实现并认识到计划和政策中所期望的未来的多样性和背景性，以及
三年制飞机文凭课程... - Bteup
1. 代数 (i) 方程理论和根的对称函数。(ii) 二项式、对数和指数级数、一般指数和对数级数（修订版）。(iii) 复数及其在工程问题中的应用。(iv) 矢量及其图形表示矢量的数学运算。(v) 矩阵和行列式（基本概念）。 2. 三角学 (i) 反圆函数。(ii) 德莫维尔定理及其应用。 3. 微分学：(i) 求函数微分系数导数的方法。(ii) 函数的微分。(iii) 对数微分。(iv) 逐次微分。(v) 偏微分。(vi) 切线和法线的应用。(vii) 最大值和最小值 4. 积分学 (i) 不定积分的方法。 (ii) 代换积分。 (iii) 分部积分。 (iv) 积分在圆柱体、圆锥体和球体的表面积、面积和体积计算中的应用。
练习表4：图和量子通道
您可能已经注意到，即使是简单的计算，也很难轻松地遵循，甚至很难遵循量的张力因素。因此，开发了一种视觉计算的替代方法。我们将在本练习中简要介绍该计算技术的基础知识。但是，我们鼓励您查看https://arxiv.org/abs/1912.10049，该概述对Tensor Networks提供了一个很好而完整的概述。在本课程中，您不需要大部分内容。在张量网络表示法中，张量只是一个具有索引的对象，通常是一组复数a i 1，...，i n。带有一个索引的张量是向量，带有两个索引的张量是矩阵。带有n个指数的张量表示为带N腿的盒子。我们在我们已经知道的对象和图表之间具有以下对应关系。首先，我们将使用线的方向区分状态的KET和胸罩（与向量相对应）：
练习表 4：图表和量子通道
您可能已经注意到，对于少量的张量因子，即使是简单的计算也可能变得难以理解。因此，开发了一种可视化此类计算的替代方法。在本练习中，我们将简要介绍这种计算技术的基础知识。但是，我们鼓励您查看 https://arxiv.org/abs/1912.10049，它对张量网络进行了完整而全面的概述。但是，对于本课程，您不需要大部分内容。在张量网络符号中，张量只是一个具有索引的对象，通常是一组复数 A i 1 ,...,in 。具有一个索引的张量是向量，具有两个索引的张量是矩阵。具有 n 个索引的张量表示为具有 n 条腿的盒子。我们有已知对象与图表之间的以下对应关系。首先，我们将使用线的方向来区分状态（对应于向量）的 kets 和 bra：
随机量子定理
本文介绍了几类与物理学和动态系统理论密切相关的新数学结构。这些结构中最普遍的一种称为广义随机系统，它们共同包含许多重要的随机过程，包括马尔可夫链和随机动态系统。然后，本文陈述并证明了一个新定理，该定理建立了任何广义随机系统与酉演化的量子系统之间的精确对应关系。因此，该定理导致了量子理论的新表述，以及希尔伯特空间、路径积分和准概率表述。该定理还从第一原理的角度解释了为什么量子系统基于复数、希尔伯特空间、线性酉时间演化和玻恩规则。此外，该定理表明，通过选择合适的希尔伯特空间，并选择适当的幺正演化，可以在量子计算机上模拟任何广义随机系统，从而可能为量子计算开辟一系列新颖的应用。
Ureqa：利用操作感知错误率来……
背景和问题陈述。在量子计算机中，量子比特是基本单位，类似于经典比特。量子比特状态 ( | Ψ ⟩ ) 可以表示为两个基态的叠加：| 0 ⟩ 和 | 1 ⟩ 。更正式地说，| Ψ ⟩ = a | 0 ⟩ + b | 1 ⟩ ，其中 a 和 b 是复数，满足 ∥ a ∥ 2 + ∥ b ∥ 2 = 1。由于量子比特的量子物理行为，在测量时，这种叠加会崩溃，并且量子比特要么处于状态 | 0 ⟩（概率为 ∥ a ∥ 2 ），要么处于状态 | 1 ⟩（概率为 ∥ b ∥ 2 ）。可以在计算机上对一组量子比特依次执行多个操作来运行量子算法。在完成量子算法的执行后，测量所有量子比特的量子比特状态并分析输出。量子比特操作称为量子操作，有三种类型：1 量子比特门、2 量子比特门和读出。1 量子比特门对单个量子比特进行操作并改变量子比特的叠加状态。2 量子比特门
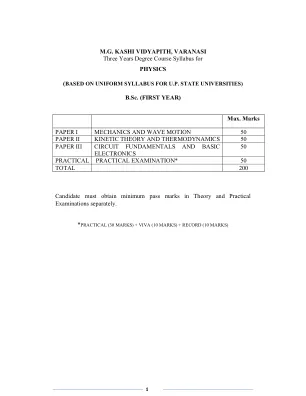
瓦拉纳西的喀什维迪亚皮特
试卷 I - 力学与波动 第一单元 惯性参考系、牛顿运动定律、直线和圆周运动中粒子的动力学、保守力和非保守力、能量守恒、线性动量和角动量、一维和二维碰撞、横截面。 第二单元 简单物体的转动能量和转动惯量、刚体在水平和倾斜平面上的平动、转动和运动的综合、陀螺运动的简单处理。弹性常数之间的关系、梁的弯曲和圆柱体的扭转。 第三单元 中心力、两粒子中心力问题、减小质量、相对和质心运动、万有引力定律、开普勒定律、行星和卫星的运动、地球静止卫星。 第四单元 简谐运动、SHM 的微分方程及其解、复数符号的使用、阻尼和强迫振动、简谐运动的合成。波动的微分方程、流体介质中的平面行进波、波的反射、反射时的相变、叠加、驻波、压力和能量分布、相速度和群速度。
量子实验和超图：量子干涉、量子计算和量子纠缠的多光子源
我们引入了超图的概念来描述具有概率多光子源的量子光学实验。每个超边代表一个相关光子源，每个顶点代表一条光输出路径。这种通用的图形描述为产生复杂的高维多光子量子纠缠态提供了新的见解，超越了通过自发参数下转换对创建所施加的限制。此外，可以通过实验研究超图的性质。例如，确定超图是否具有完美匹配的 NP 完全问题可以通过在量子实验中通过实验检测多光子事件来回答。通过在超图中引入复数权重，我们以图形方式展示了一般的多粒子量子干涉和操纵纠缠。我们的工作为多光子高维状态生成的发展铺平了道路，并可能激发使用超图映射的量子计算的新应用。