XiaoMi-AI文件搜索系统
World File Search SystemPiperton 分区条例
2.1.定义 - 除本条例另有明确定义外,本条例中使用的所有词语均有其惯常词典定义,只要与条例上下文不矛盾。“应”一词是强制性的。现在时态中使用的词语应包括将来时态;单数应包括复数,复数应包括单数;“建筑物”一词应包括“结构”一词。如果建筑规范或词典定义与本条例中的定义发生冲突,则以本条例中的定义为准。本条例中为定义允许用途而建立的类别源自《标准土地使用编码手册》,并根据 Piperton 市附属建筑的特殊需求进行了调整:在同一地块上具有通常附带性质并从属于主要用途或建筑物的用途或建筑物。就本条例而言,此类建筑物包括但不限于储藏棚、车间、卫星天线和垫子。小巷:仅提供通往相邻物业的次要途径且通行权宽度为三十 (30) 英尺或更少的通道。公寓:多户住宅中的一个单元,包括生活、烹饪和卫生设施。汽车存放场:用于停放和/或存放一辆或多辆被遗弃或扣押的可操作车辆的任何土地,并为此获得补偿。护堤:用土堆成的土丘,无论是天然的还是人造的,用于遮挡视线。寄宿公寓或宿舍:在预定的时间段内为两人或多人提供住宿和/或餐饮并收取报酬的建筑。缓冲带:为保护一种土地用途不受与其不相容的另一种土地用途影响而设立的一条土地带,该带经过景观美化并永久保留为开放空间用途。建筑物:为支撑、围护、遮蔽或保护人员、动物、动产或财产而设计或建造的任何结构。建筑物高度:从建筑物前线的完工坡度到屋顶线最高点的垂直距离。建筑物线 - 前、侧、后:根据本条例规定,定义前院、侧院和后院所需面积的线。这条线通常与地块线平行固定,相当于所需的院子。
激进聚合的共聚数据
尽管在文献中已经累积了有关共聚物和共育的大量知识,但是在共聚物中没有适当的图形用户界面(GUI)的免费数据库。专注于共聚物仅具有两种类型的单体(由于对基本面的关注)和自由基聚合中的共聚物,即最重要的聚合物ization,我们提出复数b,这是一个具有许多有用的GUI函数的共聚物数据库,包括两个:1)图形显示了两个单体和相应的共聚物之间的多个连接(具有不同的反应性比),从而有助于用户的直觉理解(图。3D和4),以及2)根据与原始单体的相似性,为每个单体对提供了替代单体的列表(图。3D和5)。我们认为,CopoldB是一种有用的资源,可以完全和全面地了解当前的共聚状态,也是促进聚合物化学研究的鼓舞人心的工具。CopoldB可通过https://www.copoldb.jp/获得。
决策和命令-Enbridge Gas Inc. EB-2022-0200
如果在此代码中定义单词或短语,则该法或电力法,语音或单词或短语的语法形式的其他部分具有相应的含义。标题仅是为了方便的,不会影响该法规的解释。导入单数的单词包括复数,反之亦然。导入性别的单词包括任何性别。导入一个人的单词包括:(i)一个人; (ii)一家公司,独资经营,合伙企业,信托,合资企业,协会,公司或其他私人或公共公司; (iii)任何政府,政府机构或机构,监管机构或机构或其他政治或大学的任何人。对一个人的引用包括该人的继任者和允许的分配。对身体的引用,无论是否法定,都将不再存在或传递到另一个身体的功能是对身体替换的人的引用,或者基本上成功地取代了其功能或功能。对文件(包括法定文书)或文件的规定的引用包括对该文件或该文件的规定的任何修正或补充。“包括”的表达方式是不受限制的。
资优教育基金:校外进阶学习计划
课程大纲 本课程旨在让资优学生了解量子计算机的运作、量子计算所使用的算法及其应用。学生将获得在桌上型量子计算机上编写和测试程序的实用技能,以供教育和研究之用。他们还可以学习和了解中国量子计算的现况以及量子物理与艺术之间的联系。此外,通过学与教活动,学生可以培养对个人成长和发展至关重要的积极价值观和态度。教育心理学家将为学生参加者讲授情感教育课。本课程分为三个阶段。 第一阶段:量子计算基础(共 36 小时) 模式:课时 学生将获得必要的数学知识(矩阵代数和复数),以理解量子计算语言、量子计算机架构、量子态和量子比特、多量子比特和纠缠、构建量子计算机的方法、量子电路、量子算法等。 教育心理学家将主持一节课,以
未来工作的五维空间
摘要。我们提出了未来工作 (FoW) 的结构化观点,使用未来学家的视角来推进两个目标:推进 FoW 的核心维度,同时概述未来学家考虑可能的未来的方法。专业未来学家指出,他们并不预测未来,而是构建多个未来——复数。这些未来观点以情景形式呈现,以帮助决策者考虑替代方案并更好地理解规划维度之间的相互作用。推动规划的情景是通过借鉴将塑造我们未来的特征或维度构建的。我们在这里介绍的就是这些维度。我们为 FoW 提供了五个基础维度,将它们表达为构成问题的对立观点:(1) 虚拟性与压缩工作安排;(2) 原子工作与整体工作;(3) 算法与人类决策;(4) 新自由主义资本主义与安全网资本主义;(5) 超人与虚无主义者。我们使用这些维度来提供场景以说明它们的用途。最后,我们反思了 2020 年疫情带来的冲击以及公司规模对未来工作的影响。
量子计算的构建模块
1. 需要一个具有良好特征的量子比特的可扩展物理系统。量子比特只是一个量子两能级系统,就像自旋为 1/2 粒子的两个自旋态,原子的基态和激发态,或单个光子的垂直和水平极化。量子比特状态的通用符号将一个状态表示为 | 0 ⟩,将另一个状态表示为 | 1 ⟩ 。量子比特与比特之间的本质区别是,根据量子力学定律,单个量子比特的允许状态填满一个二维复向量空间;一般状态写为 a | 0 ⟩ + b | 1 ⟩ ,其中 a 和 b 为复数,通常采用规范化约定 | a | 2 + | b | 2 = 1 。两个量子比特的一般状态 a | 00 ⟩ + b | 01 ⟩ + c | 10 ⟩ + d | 11 ⟩ 是一个四维向量,两个系统的每个可区分状态对应一个维度。这些状态一般是纠缠的,这意味着它们不能写成两个单独量子比特状态的乘积。n 个量子比特的一般状态由 2 n 维复向量指定
课程描述
阿拉伯ARBC 101基本阿拉伯语I 3学分学生将研究五个主要辩证区的阿拉伯文字和语音学,并获得对这些地理区域的概述。将重点放在获取阿拉伯文字,发音和学习简单对话的上。ARBC 102基本阿拉伯语II 3学分,学生将研究单数,双重和复数的语法案例系统。他们还将开始三边形和四边形自由基系统。将重点放在改善发音和学习简单对话上。先决条件:ARBC 101。arbc 201中级阿拉伯语I 3个学分,学生将提高他们在Ruq'a脚本中的阅读,翻译和写作的熟练程度。重点将放在情境对话和语法分析上。先决条件:ARBC 102。ARBC 202中级阿拉伯语II 3学分学生将提高其发音和使用阿拉伯文字的设施的能力。重点将使用简单的短文,情境对话和语法分析来讲话,阅读和写作技巧。先决条件:ARBC201。
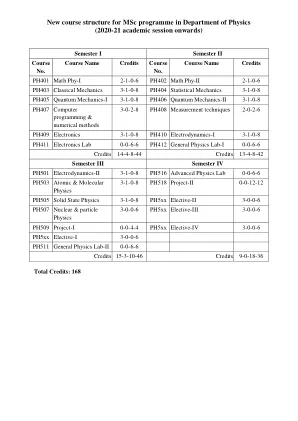
物理系理学硕士课程的新课程结构
PH401:数学物理 I (2-1-0-6) 线性代数:线性向量空间:对偶空间和向量、柯西-施瓦茨不等式、实数和复数向量空间的定义、度量空间、线性算子、子空间;跨度和线性独立性:行减少和方法;基础和维度:使用简化的跨度和独立性测试 (RREF) 方法;线性变换:图像、核、秩、基础变换、转移矩阵、同构、相似变换、正交性、Gram-Schmidt 程序、特征值和特征向量、希尔伯特空间]。张量:内积和外积、收缩、对称和反对称张量、度量张量、协变和逆变导数。常微分方程和偏微分方程:幂级数解、Frobenius 方法、Sturm-Liouville 理论和边界值问题、格林函数;笛卡尔和曲线坐标系中不同波动方程的分离变量法,涉及勒让德、埃尔米特、拉盖尔和贝塞尔函数等特殊函数以及涉及格林函数的方法及其应用。教材:
金门DNA组装的自动化和微型化
量子位可以隔离以执行有用的信息理论任务,即使物理系统从根本上是由非常高维操作员代数来描述的。这是因为可以将Qubits始终嵌入更高维的Hilbert空间中。将经典概率分布的类似嵌入到量子理论中,可以通过变质出现经典物理。在这里,我们询问哪些其他概率模型可以类似地嵌入到有限的维量子理论中。我们表明,可嵌入的模型正是与欧几里得特殊的约旦代数相对应的模型:对真实,复数或四元素的量子理论以及“自旋因子”(具有三个以上自由度的量子),及其直接总和。在这些情况下,只有具有超级条例规则的经典和标准量子理论才能由物理腐蚀图产生。我们的结果通过阐明如何(或不能)伪造量子理论的某些实验测试对量子理论的某些实验测试产生了重大影响。此外,它们暗示所有不受限制的非古典模型都必须是上下文。
注册商(通过授权公司的身份验证...
定义和一般解释3。(1)这些规则中使用的定义术语及其含义在附表1(2)中包含,除非上下文另有要求 - (a)对各节的参考是《 2006年《公司法》的部分; (b)对“规则”或“规则”的引用是对这些注册服务商(授权的公司服务提供商的身份验证)规则2025的引用,并参考编号规则,章节,部分或时间表是对这些规则中的规则,章节,部分或时间表; (c)提及文件的引用包括提交或发送该文件; (d)对一项法案的提及包括对根据该法案制定的任何下属立法的提及; (e)提到立法或立法规定是对立法或立法规定的提及,因为随后可以修改(f)单数中的单词包括复数,反之亦然。(3)除非上下文另有要求,否则在这些规则中提到的信息为指定,描述,可访问或可用,或者在网站中包括在这些规则的一部分中,并且对网站的任何参考是对网站的参考,因为可能会不时地修改