XiaoMi-AI文件搜索系统
World File Search System杜尔加布尔国家技术学院
出席会议的成员如下: 1. Anupam Basu 教授:NIT Durgapur 理工学院院长兼参议院主席 2. S. Chattopadhyay 教授:NIT Durgapur 生物技术系成员 3. K. Aikat 教授:NIT Durgapur 生物技术系成员 4. Surabhi Chaudhuri 教授(女士):NIT Durgapur 生物技术系成员 5. Debjani Dutta 博士:NIT Durgapur 生物技术系主任成员 6. SS Mukhopadhyay 教授:NIT Durgapur 生物技术系成员 7. Dalia Dasgupta Mandal 教授:NIT Durgapur 生物技术系成员 8. A. Dey 教授:NIT Durgapur 生物技术系成员 9. D. Sukul 教授:NIT Durgapur 化学系成员 10. AK Patra 教授:NIT 化学系成员Durgapur 11. M. Maji 教授:NIT Durgapur 化学系成员
M.Tech。嵌入式和机器学习系统课程和教学大纲-M.Sc.应用数学电子与ICT学院,NIT WARANGAL https://forms.gle/ ...
关于FDP:有关人工智能(AI)的教师发展计划(FDP),用于计算机视觉,医学成像应用将帮助教育者和研究人员了解AI基础知识及其如何应用于具有多个安全应用的医学成像技术。参与者将探索机器学习和深度学习概念,专注于使用AI进行医学成像,这有助于诊断,医疗保健,农业,零售和监视系统。AI通过基于面部识别,虹膜识别,指纹分析和语音识别的准确有效的身份验证方法,在计算机视觉中起关键作用。通过实践活动和实例实例,与会者将获得实用技能,可以在教学和研究中有效地使用不同的AI使用AI。在计划结束时,参与者将准备将AI工具集成到他们的工作中,提高他们通过现代技术教授和解决安全挑战的能力。这将通过增强他们在这些关键领域的专业知识和教学能力来使参与者受益。主要课程内容:针对计算机视觉应用程序的最新实施介绍。机器学习基础知识,使用数据预处理和数据可视化。监督和无监督的学习方法,SVM分类,神经网络和应用程序。深度学习方法的简介和基于DL的其他架构及其应用程序。用于计算机视觉,生物特征和医学成像实现的深度学习体系结构。使用Python/Matlab的动手会话。医学图像数据处理和分析。用于生物医学成像,基于CT扫描/MRI的图像分析,眼底和医学图像分类的AI/ML。对象检测/跟踪算法(例如Yolo等),诸如UNET等分段算法等使用张量流/Pytorch识别人类活动/动作/生物识别识别张量流/keras/pytorch/jupyter和colab的基础知识。使用Python/Matlab使用数据预处理和数据可视化。CV和AI算法在硬件平台上实现,例如Jetson Nano,TX2和Pynq等。主持此计划的教师:该计划将由Nit Warangal的教职员工进行;邀请来自IIT/NIT/IIIT的有关领域的院士在该计划中发表讲座。也有望作为课程的一部分提供行业的演讲者。
CARE-电子应用研究中心-印度理工学院德里分校
射频和微波(微波电路、子系统、天线等)、微电子学(量子和纳米器件、微传感器和 MEMS、高达 THz 的新型器件等)信号处理(语音处理、声学、机器学习、波形设计、阵列信号处理等)。“射频设计和技术”硕士项目的学生将获得这三个领域的基础知识,然后继续专攻其中之一。该硕士项目的特色是“实践”培训,包括硬件实验室工作以及应用型软件的技能开发。最后一年的项目占有很高的比重,许多学生所做的项目最终会发表高质量的出版物,也会做与产品开发相关的项目。从该项目毕业的学生已经准备好着手开发最先进的电子系统。
研究生手册 - 健康与人类科学学院
HONORS & AWARDS Honorable Mention, SIOP Owens Scholarly Achievement Award (Best Paper) for 2020 Carter et al., Understanding job satisfaction in the causal attitude network (CAN) model European Association for Work and Organizational Psychology (EAWOP) Best 2019 Practitioner Poster Finalist for Harris et al., Applicant Reactions to Ideal Point Measures of Personality Herbert Zimmer Award for Research Scholarship 2018 University of Georgia, I-O心理学系Donald L.授予杰出硕士论文奖学金2018年佐治亚大学,I-O心理学系DAN MACK研究奖与个体差异和选择有关的研究2017年佐治亚大学I-O心理学系
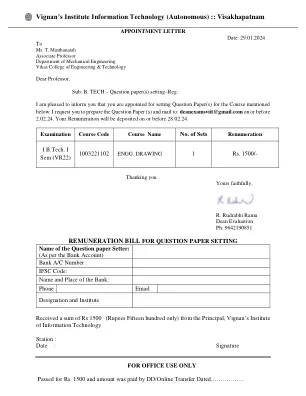
维尼昂信息技术学院(自治)
cation TE SE CC Dist contact 1 NQ R2021011 数学-III Dr.D.Ratna Babu 教授 博士 13 13 KT KRI 9000976638 2 NQ R2021011 数学-III Dr.R.Leela Vathi 助理教授 博士 10 6 HP KRI 9383455555 3 NQ R2021042 开关理论与逻辑设计 Dr K Srinivasa Rao 教授 博士 20 6 8T KRI 9494379031 4 NQ R2021043 信号与系统 Dr.T Lakshmi Narayana 副教授 博士 11 9 HP KRI 8686000546 NQ R2021044 随机变量与随机过程 Dr S Srigowri 教授 博士29 13 X4 KRI 7093322366 6 NQ R2021422 使用 Java 的面向对象编程 Dr.A.Radhika 副教授 博士 23 9 X4 KRI 9885986856 7 49 R2021011 数学-III Dr B Mahaboub 教授 博士 24 15 F0 PKS 8465977870 8 49 R2021011 数学-III Dr K Srinivas 教授 博士 28 28 8A PKS 9908786858 9 49 R2021041 电子器件与电路 Dr DVN Sukanya 副教授 博士 18 18 F0 PKS 9032869703 10 49 R2021042 开关理论与逻辑设计 Dr A Ranganayakulu 教授 博士 30 20 JU PKS 6281311010 11 49 R2021043 信号与系统 Dr M Ratnababu 教授 博士 17 10 F0 PKS 8074506708 12 49 R2021044 随机变量与随机过程 Dr P Srinivasulu 教授 博士 19 19 35 PKS 9676136356 13 7W R2021011 数学-III Dr. D Naga Bhargavi 助理教授 博士 18 18 NN GTR 9490514627
Pimpri Chinchwad工程学院
董事长30年代,电子和电信发动机Ering PCET,PIMPRI CHINCHWAD工程学院编号26,Pradhikaran,Nigdi Pune-44
14:30小时-Gujarat灾难管理学院
1。背景气候变化是由于全球温度升高引起的温室效应引起的,对古吉拉特邦面临重大挑战。该地区经历了许多与气候相关的影响,包括平均温度的迅速升高,云覆盖率和降水模式的改变,极端气候条件,海洋温度上升和海平面。这些气候变化涉及在整个州,尤其是在沿海地区施加持续的压力,加剧了现有的脆弱性,并需要采取紧迫的行动以整合适应措施和缓解策略。鉴于居住在海岸线附近的大量人口,尤其是古吉拉特邦(Gujarat),因此需要积极适应以应对气候变化影响的需求是当时的最大需求。许多人认为气候变化是21世纪的首要挑战之一,强调了负责监测此类地区的政府机构迅速采取行动的重要性。将气候适应性纳入沿海管理实践对于减轻气候变化的影响并维护古吉拉特邦的社区和生态系统的福祉至关重要。极端天气对古吉拉特邦古吉拉特邦(Gujarat Gujarat)的影响,其海岸线延伸1,663公里,在40个沿海talukas的990万居民所在地,拥有印度最长的海岸线(人口普查,2011年)。气候变化引起的温度变化预计会加剧,世界银行预计到2050年,古吉拉特邦26个地区的19个地区中,世界银行的温度升高为2-2.5°C,使他们的气候变化热点。该地区对海平面上升,旋风,盐水入侵的敏感性以及鱼产卵模式的转移预示着未来的未来迁移和由于气候变化而引起的社区流离失所,如《联合国世界移民报告》(2020年)所强调。古吉拉特邦的主要气候变化危害包括温度,降水和海平面的极端,每种都会对基础设施,人口人群,各种经济部门和农业产生各种影响。农业与劳动人口的50%吸引了9.5%的农业,对美国的GDP贡献了9.5%,面临着脆弱性的增强,热应激和草地减少了可能减少牲畜和畜牧业的产量,影响该地区的2690万牲畜人口。此外,对于民众日常需求的很大一部分,森林通道仍然至关重要。古吉拉特邦的独特生态系统,尤其是在环境脆弱的库奇奇和索拉什特拉地区,面临着气候变化,荒漠化和栖息地丧失的风险,强调迫切需要全面适应和缓解策略。
BIM第五学期教学大纲2024.pdf-管理学院
单元4。知识表示14 LHS。Definition and importance of Knowledge, Issues in Knowledge Representation, Knowledge Representation Systems, Properties of Knowledge Representation Systems, Types of Knowledge Representation Systems: Semantic Nets, Frames, Conceptual Dependencies, Scripts, Rule Based Systems(Production System), Propositional Logic, Predicate Logic, Propositional Logic(PL): Syntax, Semantics, Formal logic-connectives, truth tables, tautology, validity, well-formed-formula,使用分辨率,向后链式和前进的推理,谓词逻辑:FOPL,语法,语义,语义,定量,与FOPL的推断:通过转换为PL(存在和普遍实例化),统一和提升,使用分辨率,使用不确定的知识来处理不确定的知识,辐射变量,先前和后网络,使用完整的范围,使用完整的范围,bayes bay obles,bayes bay obles,bays bay obles,bayes bay obles,bayes obles of bay bay bays bay bay bay'模糊逻辑:模糊集,模糊集中的会员资格,模糊规则基础系统。
大脑思维学院HelixScreen创造了乳腺癌护理的新时代什么是Bose-Einstein冷凝物?冷原子...
Bose-Einstein冷凝物的研究很重要,因为它具有原子理的潜力。可以提高精度的原子激光器和测量仪器。 例如,BEC可用于精确的重力波检测。 bec还具有减速光的能力,并且已经表明,光脉冲甚至可能被困在它们中。 这可能会导致在基于光的技术领域的充分应用,并影响量子计算的世界。 总的来说,在ISS的CAL中研究更长的BEC的能力肯定会带来令人兴奋的机会。可以提高精度的原子激光器和测量仪器。例如,BEC可用于精确的重力波检测。bec还具有减速光的能力,并且已经表明,光脉冲甚至可能被困在它们中。这可能会导致在基于光的技术领域的充分应用,并影响量子计算的世界。总的来说,在ISS的CAL中研究更长的BEC的能力肯定会带来令人兴奋的机会。