XiaoMi-AI文件搜索系统
World File Search System支出计划——制定基于预算的计划
o 开始日期和结束日期:根据预算期填写这些内容。 o 预算:可与支出计划自动匹配的发票总额。 o 最大发票数量:定义可与支出计划自动匹配的发票数量。 o 最大发票总额:可与支出计划自动匹配的单张发票的最大总额。 • 单击重复行向计划添加更多行。 • 单击附件选项卡 > 将任何支持文档附加到此支出计划。 • 转到页面底部的编码部分 > 单击添加第一个编码行 > 填写所需的编码行字段。 • 单击发送以进行验证以供审批。
CIPL 对欧盟委员会关于《人工智能法案》草案的咨询的回应 CIPL 1 欢迎就欧盟委员会关于《欧洲人工智能法案》2(“AI 法案”或“法案”)的提案进行咨询,以将其纳入欧盟立法程序。CIPL 很高兴看到《人工智能法案》采纳了 CIPL 关于采用基于风险的方法监管欧盟人工智能的文件中提出的几项建议。3 这些建议旨在培养对人工智能的信任,而不会妨碍其负责任的发展。特别是,CIPL 欢迎该法案基于风险的方法,该方法将适用于高风险的人工智能用例,而不会监管人工智能技术本身或整个行业。CIPL 还欢迎拟议使用统一标准和行业自我评估产品符合性,因为这些机制已被证明能够成功推动创新并在欧盟市场开发安全可信的技术。CIPL 还欢迎旨在支持创新的措施,特别是通过为监管沙盒提供法定基础。最后,CIPL 很高兴看到《人工智能法案》中概述的一些要求与一些现有的行业惯例相一致,这些惯例为确保负责任地开发和使用人工智能设定了高标准。4 然而,CIPL 遗憾的是,《人工智能法案》没有充分考虑到一些必要条件,例如提供基于结果的规则;明确允许组织根据人工智能系统的风险和收益来调整对要求的遵守情况;奖励和鼓励负责任的人工智能实践;利用监管沙盒的经验教训;并澄清《人工智能法案》的监督和执行条款也应基于风险。CIPL 重申,要使《人工智能法案》有效地保护基本权利,同时也为欧盟创新的新时代奠定基础,它需要足够灵活以适应未来的技术。此外,该法案不能过于严格,以免抑制包括公共卫生或环境在内的一系列行业和部门对人工智能的宝贵和有益的创新和使用。最后,《人工智能法案》将受益于有针对性的调整,以更好地明确人工智能提供者、部署者和用户的责任平衡,特别是对于通用人工智能和开源人工智能模型。
CIPL 对欧盟委员会关于《人工智能法案》草案的咨询的回应 CIPL 1 欢迎就欧盟委员会关于《欧洲人工智能法案》2(“AI 法案”或“法案”)的提案进行咨询,以将其纳入欧盟立法程序。CIPL 很高兴看到《人工智能法案》采纳了 CIPL 关于采用基于风险的方法监管欧盟人工智能的文件中提出的几项建议。3 这些建议旨在培养对人工智能的信任,而不会妨碍其负责任的发展。特别是,CIPL 欢迎该法案基于风险的方法,该方法将适用于高风险的人工智能用例,而不会监管人工智能技术本身或整个行业。CIPL 还欢迎拟议使用统一标准和行业自我评估产品符合性,因为这些机制已被证明能够成功推动创新并在欧盟市场开发安全可信的技术。CIPL 还欢迎旨在支持创新的措施,特别是通过为监管沙盒提供法定基础。最后,CIPL 很高兴看到《人工智能法案》中概述的一些要求与一些现有的行业惯例相一致,这些惯例为确保负责任地开发和使用人工智能设定了高标准。4 然而,CIPL 遗憾的是,《人工智能法案》没有充分考虑到一些必要条件,例如提供基于结果的规则;明确允许组织根据人工智能系统的风险和收益来调整对要求的遵守情况;奖励和鼓励负责任的人工智能实践;利用监管沙盒的经验教训;并澄清《人工智能法案》的监督和执行条款也应基于风险。CIPL 重申,要使《人工智能法案》有效地保护基本权利,同时也为欧盟创新的新时代奠定基础,它需要足够灵活以适应未来的技术。此外,该法案不能过于严格,以免抑制包括公共卫生或环境在内的一系列行业和部门对人工智能的宝贵和有益的创新和使用。最后,《人工智能法案》将受益于有针对性的调整,以更好地明确人工智能提供者、部署者和用户的责任平衡,特别是对于通用人工智能和开源人工智能模型。
为医疗领域的人工智能奠定基础
人工智能 (AI) 有可能使医疗保健更加有效、高效和公平。从临床决策和公共卫生,到生物医学研究和药物开发,再到卫生系统管理和服务重新设计,AI 应用正在兴起。COVID-19 大流行是催化剂,但它也是现实的检验,凸显了现有 AI 系统的局限性。大多数医疗领域的 AI 实际上都是狭义人工智能,旨在根据来自单一环境的先前整理的数据完成非常具体的任务。在现实世界中,健康数据并不总是可用、标准化或易于共享的。有限的数据阻碍了 AI 工具为可能非常复杂的不同人群生成准确信息的能力。拥有适当的患者数据对于 AI 工具至关重要,因为基于具有偏差或不完整数据的模型的决策可能会使患者面临风险。政策制定者应警惕围绕 AI 的炒作,并确定并关注 AI 可以帮助解决的实际问题和机会。在为 AI 奠定基础以帮助实现卫生政策目标时,一个关键优先事项是通过更好的数据治理以安全的方式提高数据质量、互操作性和访问。更广泛地说,政策制定者应努力实施和实施经合组织的人工智能原则,并投资于技术和人力资本。基于所有利益相关者之间包容和广泛对话的强大政策框架也是确保人工智能为患者和社会增加价值的关键。影响临床和公共卫生决策的人工智能应谨慎引入。最终,必须管理高期望,但应该追求真正的机会。
为卢旺达的新知识经济奠定基础
OPF 是一个需求主导的奖学金计划,与政府合作提供法律能力支持和发展。我们通过奖学金、网络和学习来实现这一目标。我们寻找高绩效的法律顾问,在现行政府系统和流程中工作两年,以便他们的工作有助于持续的政策制定,而不是创建并行结构来完成工作。通过为政府提供他们自己定义和要求的关键支持,我们实现了可持续的、本地拥有的发展影响。我们还拥有一个政府从业人员网络,他们在法律和公共政策的交汇处工作,促进政府和更广泛社区之间的知识共享和学习文化。
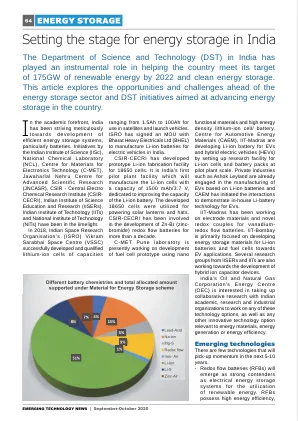
为印度的能源存储奠定基础
功能材料和高能量密度锂离子电池。印度理工学院马德拉斯分校汽车能源材料中心 (CAEM) 正在通过建立中试规模的锂离子电池和电池组研究设施,开发用于电动汽车和混合动力电动汽车 (HEV) 的锂离子电池。Ashok Leyland 等私营企业已开始制造基于锂离子电池的电动汽车,而 CAEM 已启动互动,以展示用于电动汽车的内部锂电池技术。印度理工学院马德拉斯分校一直致力于研究钒-氧化还原液流电池的电极材料和新型氧化还原对。印度理工学院孟买分校主要致力于开发用于电动汽车应用的锂离子电池和燃料电池的储能材料。来自 IISER 和 IIT 的几个研究小组也在致力于开发混合离子电容器装置。印度石油天然气公司的能源中心 (OEC) 有意与印度学术、研究和工业组织开展合作研究,研究这些技术方案以及与能源材料、能源生产或能源效率相关的任何其他创新技术方案。
营养依赖性RNA聚合酶II延伸率控制通过选择性多聚腺苷酸化调节特定基因表达程序
RNA 聚合酶 II (RNAPII) 转录是一个动态过程,延伸率经常变化。然而,RNAPII 延伸动力学变化的生理相关性仍不清楚。我们在此表明,在酵母中,降低转录延伸率的 RNAPII 突变体会导致替代性多聚腺苷酸化 (APA) 发生广泛变化。我们揭示了 APA 影响慢突变体中基因表达的两种机制:3 ′ UTR 缩短和上游干扰非编码 RNA 的过早转录终止导致的基因去抑制。令人惊讶的是,受这些机制影响的基因富含涉及磷酸盐吸收和嘌呤合成的功能,这些过程对于维持细胞内核苷酸池至关重要。由于核苷酸浓度调节转录延伸,我们的研究结果表明 RNAPII 是核苷酸可用性的传感器,并且对核苷酸池维持很重要的基因已采用响应降低转录延伸率的调节机制。
用于确定基因变异临床可行性的精准肿瘤学知识库综述
肿瘤基因检测和靶向癌症治疗的普及促进了肿瘤学领域精准医疗的发展。精准肿瘤学知识库提供了一种组织临床相关遗传信息的方法,肿瘤学家和患者都可以轻松访问,从而促进基于遗传的临床决策。许多组织和公司已经建立了精准肿瘤学知识库,供多个用户使用。一般来说,这些知识库提供有关癌症相关遗传变异的信息以及它们相关的诊断、预后和治疗意义,但它们在信息管理、设计和用户体验方面往往有所不同。建议肿瘤学家在实践中使用多个知识库,使它们相互补充。未来,需要向共同的标准和格式靠拢,以确保所有来源的综合知识能够统一,使肿瘤学界更接近实现精准肿瘤学的目标。
医疗保健的价值为医疗体系奠定基础...
因此,公众开始对许多医疗机构失去信心(或已经失去信心)是有道理的。我们需要将脱离的利益相关者重新纳入系统,专注于基于价值的医疗保健,并决心相互合作,随着时间的推移提高医疗保健价值。基于价值的医疗保健是我们家门口的革命。作为大型医疗保健组织的领导者,这些组织充满了才华横溢、充满激情的个人,他们每天都来工作,以开发更好的方法来改善我们同胞的健康,我们渴望接受一个关注对患者和社会都重要的结果的新现实。根本问题不仅是“这种变化意味着什么?”或“什么时候会发生?”而且是“我们如何实现它?”解决最后一个问题是世界经济论坛与波士顿咨询集团合作开展的“医疗保健价值”项目的重点。
ITS 伸缩塔系统 ~ 移动和固定基础...
ITS 伸缩格构钢塔结构是全自动的,延伸高度范围为 +38’0” (12m) 至 +130’0” (40m) 高于地面 (AGL),标准有效载荷能力为 550lbs (250kg) 和 650lbs (295kg),具体取决于型号配置,并提供任何同类塔系统的最大风荷载能力。虽然所有 ITS 伸缩结构都可以在其最大延伸高度单独用于自支撑配置 ~ 不需要拉线,最高可达有效载荷、风荷载和风速的组合;与所有此类塔一样,在无人值守的场地长期部署时,通常始终建议使用拉线组件 ITS 结构是定制制造的,可直接安装到混凝土基础上,或集成到众多 ITS 拖车、卡车、滑橇或其他类似平台上。可利用由业界认可的独立结构工程和咨询公司执行和认证的严格有限元分析程序进行应力分析审查,以确定塔构件设计是否符合 ANSI/TIA-EIA 222-G 标准要求,适用于每个客户特定的负载配置。格构塔构件的建模采用梁单元作为支柱构件,桁架单元作为支撑,缆索单元作为升降和支撑缆索。构件的结构参数和几何形状包含在塔建模中。计算不同风向的风荷载,然后将其作为外部荷载施加在结构上,内部确定自重荷载。为了获得所有塔构件和拉线(如果使用)中发生的最大应力,需要考虑相对于塔和可选拉线的三个不同风向(迎风、顶风、平行风)。