XiaoMi-AI文件搜索系统
World File Search System形头
SD/ - 头，PBMD＆Head，无人机
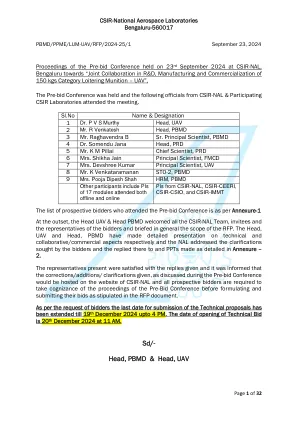
参加竞标前会议的准投标人名单是根据Annexure-1的一开始，无人机和PBMD负责人欢迎所有CSIR-NEN团队，Invitees和Bidders的代表，并在RFP的总体范围内进行了简报。头部，无人机和头部，PBMD分别对技术和协作/商业方面进行了详细的介绍，NAL解决了投标人所寻求的澄清，并回复了在附件中详细介绍的PPT -2。在场的代表对给出的答复感到满意，并获悉，在竞标前会议上进行的更正/加法/澄清将在CSIR-NAN网站上主持，所有潜在的竞标者都必须认识到对竞标会议的会议记录，然后在规定和提交其竞标文档，并提交竞标文件。根据投标人的要求，提交技术建议的最后日期已延长到2024年12月19日至下午4点。技术竞标的日期是2024年12月20日上午11点。
生物膜形成对微塑性
文学：Rummel，C.D.，Jahnke，A.，Gorokhova，E.环境。SCI。 技术。 Lett。 4（7），258 - 267 Zettler，E。R.，T。J. Mincer和L. A. Amaral-Zettler（2013）。 “ plastisphere”中的生命：塑料海碎片上的微生物群落。” 环境科学技术47（13）：7137-7146。 Gewert，B.，M。M. Plassmann和M. MacLeod（2015）。 “在海洋环境中漂浮的塑料聚合物降解的途径。” 环境SCI过程影响17（9）：1513-1521。SCI。技术。Lett。 4（7），258 - 267 Zettler，E。R.，T。J. Mincer和L. A. Amaral-Zettler（2013）。 “ plastisphere”中的生命：塑料海碎片上的微生物群落。” 环境科学技术47（13）：7137-7146。 Gewert，B.，M。M. Plassmann和M. MacLeod（2015）。 “在海洋环境中漂浮的塑料聚合物降解的途径。” 环境SCI过程影响17（9）：1513-1521。Lett。4（7），258 - 267 Zettler，E。R.，T。J. Mincer和L. A. Amaral-Zettler（2013）。 “ plastisphere”中的生命：塑料海碎片上的微生物群落。” 环境科学技术47（13）：7137-7146。 Gewert，B.，M。M. Plassmann和M. MacLeod（2015）。 “在海洋环境中漂浮的塑料聚合物降解的途径。” 环境SCI过程影响17（9）：1513-1521。4（7），258 - 267 Zettler，E。R.，T。J. Mincer和L. A. Amaral-Zettler（2013）。“ plastisphere”中的生命：塑料海碎片上的微生物群落。”环境科学技术47（13）：7137-7146。Gewert，B.，M。M. Plassmann和M. MacLeod（2015）。 “在海洋环境中漂浮的塑料聚合物降解的途径。” 环境SCI过程影响17（9）：1513-1521。Gewert，B.，M。M. Plassmann和M. MacLeod（2015）。“在海洋环境中漂浮的塑料聚合物降解的途径。”环境SCI过程影响17（9）：1513-1521。
Bi浓度对Sn-Bi合金变形行为的影响
研究了Sn-Bi-Cu、Sn-Bi-Ni、Sn-Bi-Zn、Sn-Bi-Sb合金的超塑性变形行为。本研究旨在测定Sn-Bi二元合金的应变速率敏感性指数m。在不同横梁速度下进行25、40、60和80 ℃拉伸试验，测定指数m。结果表明，指数m随Bi浓度和试验温度的增加而增大。在60和80 ℃时，Sn-Bi合金的指数m均超过了3.0，这是超塑性变形行为的阈值。研究发现，Sn-Bi共晶组织对亚共晶Sn-Bi合金的超塑性变形有显著的影响。
特刊 - 分形和分数
分数演算在机器学习和生物医学工程中的应用是一个新颖且快速增长的研究领域。分数演算（FC）与机器学习（ML）和生物医学工程（BME）的交集是一个新兴领域，有望彻底改变我们在数据分析，信号处理，生物医学系统建模和控制方面解决问题的方式。该特刊旨在将FC应用于ML和BME领域的领域中的尖端研究和发展，包括但不限于以下内容：FC的理论进步及其对ML和BME的含义；开发对机器学习和重新学习的范围的分数算法的开发；包括Neural Intervers in Neural Intervers in Neural Interials fr Fr Fring; FRIF;和图像分析；使用分数阶微分方程对生物系统进行建模；生物医学设备和机器人技术中的分数控制系统；分数演算在生理建模和生物信息信息学中的应用；在FC与ML和BME集成中的挑战和未来方向。
从量子纠缠到共形场论
2 诊断工具箱：量子纠缠和共形场论.......................................................................................................................................................................................................................................5 2.1 量子纠缠....................................................................................................................................................................................................................................................................6 2.1.1 纠缠：不可分离性....................................................................................................................................................................................................................................................6 2.1.1 纠缠：不可分离性.................................................................................................................................................................................................................................................... 6 2.1.2 冯·诺依曼纠缠熵..................................................................................................................................................8 2.1.3 纠缠缩放..................................................................................................................................................................................10 2.1.4 协方差矩阵方法..................................................................................................................................................................................15 2.2 共形场论..................................................................................................................................................................................15 . . . . 19 2.2.1 共形不变性 . . . . . . . . . . . . . 19 2.2.2 希尔伯特空间形式 . . . . . . . . . . . . . . 22 2.2.3 最小模型 . . . . . . . . . . . . . . . . . 25 2.2.4 一个例子：格子伊辛模型 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .三十七