XiaoMi-AI文件搜索系统
World File Search System量子晶格系统的准局限性边界。第二部分。无挫折自旋模型的扰动
摘要。我们研究了相对于由无挫败的汉密尔顿人定义的量子自旋系统的一系列广泛的乱态地面阶段的稳定性。这项工作的核心结果是使用Bravyi-Hastings-Michalakis(BHM)策略的证明,该策略在局部拓扑量子秩序(LTQO)的条件下,在长距离衰减的扰动下,大量差距稳定,而长距离衰减的速度比伸展的指示更快。与以前的工作相比,我们扩展了可以处理的挫败感 - 自由量子自旋模型,包括具有更通用边界条件的模型以及具有离散对称性破坏的模型。详细的估计值使我们能够为系统尺寸均匀且在某种程度上明确的间隙的正下限的有效性制定有效条件。,我们在Michalakis和Zwolak的方法下提供了BHM策略的调查,并引入了更改,以适应更一般性的一般性边界条件和更一般的晶格。我们通过不明式的半径来表达称为LTQO的基本条件,我们引入了。使用统一的有限体积结果,然后继续研究热力学极限。我们首先研究了独特的限制基态的情况,然后考虑了自发断裂离散对称性的模型。在后一种情况下,LTQO不能容纳所有本地观察到。然而,对于预先使用对称性的扰动,我们显示了间隙的稳定性和破碎的对称阶段的结构。我们证明,与每个纯状态相关的GNS Hamiltonian具有高于基态的非零光谱差距。
挫折期间的功能连接
易怒性削减了许多儿科疾病,是儿童精神病学的常见投诉;但是,其神经机制尚不清楚。一种核心的病理生理学来定义易怒的反应异常,对令人沮丧的非奖励。在这里,我们进行了一项初步的FMRI研究,以检查令人沮丧的非奖励期间功能连通性预测转诊样本中易怒的能力。这项研究包括69名年轻人(平均年龄= 14.55岁),诊断组的易怒水平不同:颠覆性情绪失调障碍(n = 20),注意力激发/多动障碍(n = 14),焦虑症(n = 12)(n = 12)(n = 12)和对照组(n = 23)。在fMRI期间,参与者完成了令人沮丧的认知灵活性任务。通过操纵任务困难而引起了挫败感,以至于在需要认知能力的试验中,“挫败感”块具有50%的误差率和一些操纵的反馈,而“非施工”块的误差率为10%。挫败感和非施工块被随机散布。儿童和父母报告情感反应性指数用作易怒的维度措施。基于连接组的预测建模,一种机器学习方法,进行了十倍的交叉验证,以识别预测易怒的网络。在挫败感(但不是非施工)中的连通性预测儿童报告的烦恼(ρ= 0.24,根平方误差= 2.02,p = 0.03,置换测试,1000次迭代,单尾)。对年龄,性别,药物,运动,多动症和焦虑症状的结果进行了调整。烦恼的预测网络主要在运动感官网络中;在运动感官,皮层和显着性网络中;在这些网络以及额叶和内侧额叶网络之间。这项研究提供了初步证据,表明易怒性的个体差异可能与挫折过程中的功能连通性有关,这是一种与表型相关的状态。
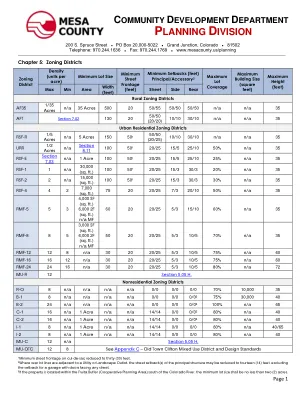
表格-挫折和现场规划说明.pdf
下列内容必须包含在必需的场地规划中: 带有尺寸的地产界线轮廓 拟建结构的轮廓,该轮廓用交叉影线标出“拟建建筑” 拟建结构与街道、后方和侧面地产界线(退让线)的距离 地产上所有现有的结构 地产相邻的所有街道和街道名称 地产上的所有地役权和通行权 所有现有和拟建的车道