XiaoMi-AI文件搜索系统
World File Search SystemEE-电气与计算机工程
EE 743. 工程中的数值方法。3 小时。本课程涵盖了广泛工程应用和数据分析的数值方法理论和实践。主题包括数值微积分、线性代数和优化。学生将接触到卷积神经网络、压缩感知、特征脸、稳定性、主成分分析、k 均值聚类、使用活动轮廓进行图像分割、噪声中信号检测和函数拟合等现代主题。本课程提供编程数值分析算法的实践经验。
M.Tech程序 - 计算机辅助D机械...
M.Tech。 计算机辅助设计(全职课程)学期 - I EME-501数值方法和计算机编程5(3-2-0)代数和超验方方程的单位1解决方案:牛顿 - 拉夫森方法,包括复杂根的方法,包括Graeffe的方法,Graeffe的根平方方法(基于计算机的Algorithm and Algorithm and groming for thulgorith and Algorithm and Amprog)。有限差异的插值公式,高斯的前进和向后插值公式,贝塞尔和拉普拉斯 - 埃弗莱特的公式,立方样条,使用Chebyshev多项式的最小二乘近似。 单元3线性同时方程的解:Cholesky's(Crout)方法,高斯 - 西德尔迭代和放松方法,特征值问题的解决方案;最小,最大和中间特征值(这些方法的基于计算机的算法和程序)单位-4数值分化和集成:使用差异操作员的数值差异化,Simpson的1/3和3/8规则,Boole的规则,Weddle的规则。 单位-5差分方程解:修改后的Euler方法,2 nd,3 rd和4 orders的runge-kutta方法,预测器 - 矫正器方法,普通微分方程的稳定性,Laplace's的溶液和Liebmann方法的poisson方程解决方案。 Text Books: 1. M. K. Jain, S.R.K. iyenger和R.K. Jain,“科学和工程计算的数值方法”,Wiley Eastern Ltd. 2. S. K. Gupta,“工程师的数值方法”,Wiley Eastern Ltd. 3。 B. S. Grewal,“数值方法”,Khanna出版物。 4。 A. D. Booth,“数值方法”,学术出版社,纽约5。M.Tech。计算机辅助设计(全职课程)学期 - I EME-501数值方法和计算机编程5(3-2-0)代数和超验方方程的单位1解决方案:牛顿 - 拉夫森方法,包括复杂根的方法,包括Graeffe的方法,Graeffe的根平方方法(基于计算机的Algorithm and Algorithm and groming for thulgorith and Algorithm and Amprog)。有限差异的插值公式,高斯的前进和向后插值公式,贝塞尔和拉普拉斯 - 埃弗莱特的公式,立方样条,使用Chebyshev多项式的最小二乘近似。单元3线性同时方程的解:Cholesky's(Crout)方法,高斯 - 西德尔迭代和放松方法,特征值问题的解决方案;最小,最大和中间特征值(这些方法的基于计算机的算法和程序)单位-4数值分化和集成:使用差异操作员的数值差异化,Simpson的1/3和3/8规则,Boole的规则,Weddle的规则。单位-5差分方程解:修改后的Euler方法,2 nd,3 rd和4 orders的runge-kutta方法,预测器 - 矫正器方法,普通微分方程的稳定性,Laplace's的溶液和Liebmann方法的poisson方程解决方案。Text Books: 1.M. K. Jain, S.R.K.iyenger和R.K. Jain,“科学和工程计算的数值方法”,Wiley Eastern Ltd. 2.S. K. Gupta,“工程师的数值方法”,Wiley Eastern Ltd. 3。B. S. Grewal,“数值方法”,Khanna出版物。4。A. D. Booth,“数值方法”,学术出版社,纽约5。K.E. ATKINSON,“数值分析概论”,John Wiley&Sons,NY EME-503固体的高级力学4(3-1-0)单位1:压力和应变分析,组成型关系,失败理论。 单元2:非圆形切片的扭转,平面应力和平整应变问题,疲劳分析的综述。 单元3:裂缝力学,非弹性行为,粘弹性,聚合物单元4:的结构和行为,单向复合材料和正性层层的行为,纤维复合材料的故障理论,在复合材料中的各种结构的发展,基于计算机的分析和固体的分析和解决方案的解决方案K.E.ATKINSON,“数值分析概论”,John Wiley&Sons,NY EME-503固体的高级力学4(3-1-0)单位1:压力和应变分析,组成型关系,失败理论。单元2:非圆形切片的扭转,平面应力和平整应变问题,疲劳分析的综述。单元3:裂缝力学,非弹性行为,粘弹性,聚合物单元4:的结构和行为,单向复合材料和正性层层的行为,纤维复合材料的故障理论,在复合材料中的各种结构的发展,基于计算机的分析和固体的分析和解决方案的解决方案
量子聚类的全面分析:寻找所有潜在的最小值
量子聚类 (QC) 是一种基于量子力学的数据聚类算法,通过用高斯函数替换给定数据集中的每个点来实现。高斯函数的宽度为 𝜎 值,这是一个超参数,可以手动定义和操纵以适应应用。数值方法用于查找与聚类中心相对应的量子势的所有最小值。在此,我们研究了表达和查找与二维量子势的最小值相对应的指数多项式的所有根的数学任务。这是一项杰出的任务,因为通常无法通过分析解决此类表达式。但是,我们证明,如果所有点都包含在大小为 𝜎 的方形区域中,则只有一个最小值。这个界限不仅在通过数值方法寻找解决方案的数量方面有用,它还允许提出一种“每个块”的新数值方法。该技术通过将某些粒子组近似为加权粒子来减少粒子数量。这些发现不仅对量子聚类问题有用,而且对量子化学、固体物理和其他应用中遇到的指数多项式也有用。
计算流体动力学各向异性网格自适应十年进展
在科学计算中,网格被用作所考虑的数值方法的离散支持。因此,网格极大地影响了数值方法的效率、稳定性和准确性。各向异性网格自适应的目标是生成适合应用和数值方案的网格,以获得最佳解决方案。因此,这是一个活跃的研究领域,正在不断进步。这篇评论文章提出了自 2000 年以来 INRIA Gamma3 团队在应用于计算流体动力学中无粘性流动的各向异性网格自适应领域的研究活动的综合。它展示了这一时期理论和数值结果的演变。最后,讨论了未来十年的挑战。
生物学,技术和商业数学课程的模块手册
2个学士学位课程的数学模块5 2.1分析i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5 2.2分析II。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 6 2.3分析iii。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。5 2.2分析II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。6 2.3分析iii。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。7 2.4分析IV。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 8 2.5线性代数i。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 9 2.6线性代数II。 。 。 。 。 。 。 。 。 。 。7 2.4分析IV。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8 2.5线性代数i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。9 2.6线性代数II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10 2.7句子性理论。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。11 2.8统计i。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12 2.9统计II。 。 。 。 。 。12 2.9统计II。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。13 2.10线性优化和选定的主题。。。。。。。。。。。。。。。。。。。。。。。。14 2.11分析的数值方法。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。15 2.12线性代数的数值方法。。。。。。。。。。。。。。。。。。。。。。。。。。16 2.13实际研究阶段。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。17 2.14学士学位论文。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。18 2.15 Bachelorkolloquium。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。19
结构动力学中的数值集成 - 杜克人
用于整合运动方程的数值方法根据其准确性和稳定性进行评估和评估。通常,准确性和稳定性取决于系统模型中最短自然时期的时间步长的比率。对于具有许多坐标的系统(n> 10 3),最短的自然周期可能比基本自然时期短得多,T N /T 1> 10 4。通常,数值模型的最高几个模式的响应在物理上是毫无意义的,应该微不足道的,但潜在地抑制了,并且可以主导数值集成中的误差。这些注释中描述的显式数值方法可以人为地添加数值阻尼以抑制较高模式响应的不稳定性。隐式数值集成方法无条件稳定。
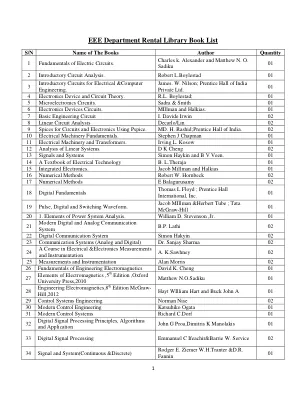
EEE 系租赁图书馆图书清单
4 电子设备和电路理论。RL Boylestad;01 5 微电子电路。Sadra 和 Smith 01 6 电子设备电路。MIllman 和 Halkias。01 7 基础工程电路 I。Davide Irwin 02 8 线性电路分析 Decarlo/Lin 02 9 使用 Pspice 的电路和电子设备的 Spice。MD. H. Rashid;Prentice Hall of India。02 10 电机基础。Stephen J Chapman 01 11 电机和变压器。Irving L. Kosow 01 12 线性系统分析。DK Cheng 02 13 信号与系统 Simon Haykin 和 BV Veen。01 14 电气技术教科书 BLTheraja 01 15 集成电子学。 Jacob Millman 和 Halkias 01 16 数值方法 Robert W. Hornbeck 02 17 数值方法 E Balagurusamy 02
无约束函数的优化:一维...
其中上标 k 表示迭代次数,el 和 e2 是预先指定的容差或精度标准。如果 f (x) 有一个简单的闭式表达式,则分析方法可以得到精确解,即最优 x 的闭式表达式 x*。如果 f(x) 更复杂,例如,如果它需要几个步骤来计算,则必须使用数值方法。非线性优化软件现在非常普及,几乎总是使用数值方法。例如,Microsoft Excel 电子表格中的“求解器”可以解决线性和非线性优化问题,并且还有许多 FORTRAN 和 C 优化器可用。第 8.9 节讨论了通用优化软件。分析方法通常难以应用于具有多个变量的非线性目标函数。例如,假设要最小化非线性函数 Ax) = f (xl, x2, . . . , xn)。要使用的必要条件是