XiaoMi-AI文件搜索系统
World File Search System利用多保真高斯过程回归对具有几何不确定性的翼型进行多目标设计优化 ⋆
摘要。本文介绍了 MH114 高升力翼型的多目标优化。我们寻求一组帕累托最优解,使翼型升力最大化,阻力最小化。由于几何不确定性,升力和阻力被认为是不确定的。概率气动力值的不确定性量化需要大量样本。然而,由于 Navier-Stokes 方程的数值解,气动力的预测成本很高。因此,采用多保真替代辅助方法将昂贵的 RANS 模拟与廉价的潜在流量计算相结合。基于多保真度替代方法使我们能够在不确定的情况下经济地优化机翼的气动设计。
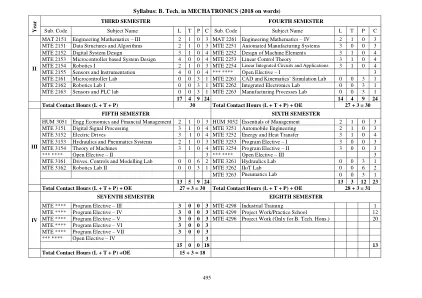
教学大纲:机电一体化技术学士学位(2018 字)
向量微积分:梯度、散度和旋度,它们的物理意义和恒等式。线、表面和体积积分。格林定理、散度陈述和斯托克斯定理、应用。傅里叶级数:周期函数的傅里叶级数、欧拉公式。奇函数、偶函数和任意周期函数的傅里叶级数。半程展开。傅里叶积分。正弦和余弦积分、傅里叶变换、正弦和余弦变换。谐波分析。偏微分方程:基本概念、仅涉及一个变量的导数的方程解。通过指示变换和变量分离求解。用分离变量法推导一维波动方程(振动弦)并求其解。达朗贝尔波动方程解。用高斯散度定理推导一维热方程并求一维热方程解。用分离变量法求解。数值方法:一阶和二阶导数(常导数和偏导数)的有限差分表达式。边界值问题的解,二阶偏微分方程的分类。用标准五点公式求拉普拉斯和泊松方程的数值解,用显式方法求热和波动方程的数值解。参考文献: 1.Kreyszig, Erwin,《高级工程数学》,John Wiley & Sons,(第 5 版),2010 年。2.3.S. S. Sastry,《数值分析入门方法》(第 2 版),1990 年,Prentice Hall。B. S. Grewal,《高等工程数学》,1989 年,Khanna Publishers 4。Murray R. Spiegel,《矢量分析》,1959 年,Schaum Publishing Co.
大电流真空二极管中“异常”电子的物理性质
简介/目的:从理论上解释亚纳秒真空二极管中存在一组电子,其动能远高于施加电压(乘以基本电荷值)qU max 。方法:采用基于 Vlasov-Poisson 微分方程组数值解的数学方法,用于各种设计的一维真空二极管。结果:详细显示了所谓的“异常”电子出现在表征真空二极管中建立电流流动过程的瞬态时间域中。结论:令人信服地表明,“异常”电子的存在与二极管设计或额外电流载体的存在无关。在电压脉冲前沿为亚纳秒的真空二极管中,超过 qU max 的能量可能超过 20%。
动态耗散参数的动态散热模型,用于油导向和空气牵引变压器及其实验验证
摘要:通常用狭窄油通道的牵引力变压器使用ODAF或“定向空气强制的油”方法冷却,在该方法中,其温度在很大程度上取决于绕组的焦油热量,变压器中的共轭热传递,以及通过油冷却器的二次热量释放,以及油泵产生的油液液泵。既不有资格预测这种类型的变压器中的时间和空间温度变化,均未获得热 - 电动类比和CFD模拟方法。 在当前工作中,分布式参数模型是为牵引力变压器和油冷却器而建立的,分别假定在油流方向上的一维温度线。 然后,这两个模型通过其界面的流量,温度和压力连续性与油泵和管道的集体参数结合,从而导致了油导向和空气牵引力变压器的动态热量耗散模型的推导。 另外,为其数值解提供了有效的算法,并进行了温度上升实验以进行模型验证。 最后,研究了牵引力变压器中动态热量耗散的基本性,并研究了环境温度的影响。均未获得热 - 电动类比和CFD模拟方法。在当前工作中,分布式参数模型是为牵引力变压器和油冷却器而建立的,分别假定在油流方向上的一维温度线。然后,这两个模型通过其界面的流量,温度和压力连续性与油泵和管道的集体参数结合,从而导致了油导向和空气牵引力变压器的动态热量耗散模型的推导。另外,为其数值解提供了有效的算法,并进行了温度上升实验以进行模型验证。最后,研究了牵引力变压器中动态热量耗散的基本性,并研究了环境温度的影响。
来自经典随机过程的非平衡量子自旋动力学
摘要 . 继我们最近的工作之后,我们研究了一种非平衡量子自旋系统的随机方法。我们展示了该方法如何应用于各种物理可观测量和不同的初始条件。我们提供了广泛适用的精确公式,用于描述量子猝灭后期望值和相关函数的时间依赖性,这些公式以经典随机过程的平均值表示。我们进一步探讨了在动态量子相变存在下经典随机变量的行为,包括它们的分布和相关函数的结果。我们详细介绍了相关随机微分方程的数值解,并研究了经典描述中波动的增长。我们讨论了随机方法当前实施的优势和局限性以及进一步发展的潜力。
量子力学中一维时间分数阶薛定谔问题的解析研究
本研究对量子力学中出现的一维时间分数阶非线性薛定谔方程进行了分析研究。在本研究中,我们建立了 Sumudu 变换残差幂级数法 (ST-RPSM) 的思想,以生成具有分数阶导数的非线性薛定谔模型的数值解。提出的思想是 Sumudu 变换 (ST) 和残差幂级数法 (RPSM) 的组合。分数阶导数取自 Caputo 意义。所提出的技术是独一无二的,因为它不需要任何假设或变量约束。ST-RPSM 通过一系列连续迭代获得其结果,并且得到的形式快速收敛到精确解。通过 ST-RPSM 获得的结果表明,该方案对于非线性分数阶模型是真实、有效和简单的。使用 Mathematica 软件以不同的分数阶级别显示一些图形结构。
受邀主题演讲嘉宾 - CoSME 会议
摘要:我们证明,尽管性质不同,但许多能量束控制深度加工工艺(例如水射流、脉冲激光、聚焦离子束)都可以使用相同的数学框架建模——偏微分演化方程,只需进行简单的校准即可捕捉每个工艺的物理特性。逆问题可以通过伴随问题的数值解有效地解决,并导致产生具有最小误差的规定三维特征的光束路径。通过使用三种在非常不同的长度尺度上操作且具有不同材料去除物理原理的工艺(水射流、脉冲激光和聚焦离子束加工)生成精确的自由曲面,证明了这种建模方法的可行性。我们的方法可用于探索各种时间相关过程的逆问题,从而实现生成具有定制属性的精确表面的阶跃变化。
利用多个信标的深空光学导航
摘要 随着发射到太空的卫星数量的增长,依赖传统辐射跟踪的地面设施已达到饱和。因此,自主导航是可持续深空任务的主要支持技术之一。本文解决了利用多个信标独立于地面估计观察者位置的深空光学导航问题。本文推导出利用多个信标的深空导航问题的最小二乘解和解析协方差。视线方向和物体星历表的扰动被纳入协方差公式。然后,阐述了扰动模型、导航解和导航协方差的几何解释。通过测试用例评估了导航精度对信标数量的敏感性,显示了数值解和解析解之间的对应关系。最后,本文展示了利用多个信标与两个最优信标的导航精度的比较。
具有滑移效应的不规则尺寸表面外 CuO-MgO/甲醇混合纳米流体的 3D MHD 非线性辐射流
对具有滑移效应的不规则尺寸薄片上的 3D MHD 非线性辐射混合纳米流体流动进行了数值研究。混合纳米流体由嵌入甲醇或甲醇 (MA) 中的氧化铜 (CuO) 和氧化镁 (MgO) 纳米颗粒组成。使用相似性将控制 PDE 改为 ODE,并使用射击方案获得数值解。通过图表和数值解释分析和反映了物质因素对传输现象的作用。同时给出了 CuO-MA 纳米流体和 CuO-MgO/MA 混合纳米流体的解。结果确定混合纳米流体和纳米流体的温度和流动边界层厚度并不是唯一的。与 CuO-MgO/MA 混合纳米流体相比,CuO-MA 纳米流体的传热作用较高。这得出结论,CuO-MgO 组合是一种良好的绝缘体。