XiaoMi-AI文件搜索系统
World File Search System通过跨学科培训和研究合作增强历史上黑人医学院的数据科学和基因组学能力
模型验证取决于预测数据和实验数据之间的一致性。但是,找到问题的解决方案,这些方程式由许多参数的方程式描述,即使是它们的数量级也不知道,这是一项艰巨的任务。这使得在多维和非线性数据的情况下,曲线拟合非常困难。本文采用混合随机和确定性方法提出了一个基于图形的用户界面程序,该程序可以通过最小化测量数据与根据数学表达式计算的数据之间的差异来轻松且可靠地确定模型参数。该程序已在多个实验室中广泛使用,事实证明,该程序在许多不同领域的模型参数中有效,例如对配体 - 受体结合的药理学研究,人群的昆虫学研究,细菌生长,光合作用,光合作用,毒理学,毒理学,差异扫描热量量表和核能均匀仪,以及核能均匀磁构成和核能。对于面对从多维和非线性数据估算模型参数的问题的研究人员来说,这是一个有效的解决方案,参数尚不清楚。
2H -MOS2纳米片的共价交联 - 数字CSIC
二维(2D)材料,例如,由自组装的分子单层或通过单层范围材料的单层形成,可以与光子纳米腔有效地融合,并有可能达到强耦合方案。耦合可以使用经典的谐波振荡器模型或空腔量子电动力学哈密顿量,这些模型通常忽略单层内的直接偶极 - 偶极相互作用。在这里,我们对系统的全哈密顿量进行对角,包括这些直接的偶极偶极相互作用。对典型2D系统的光学特性的主要影响只是将单层的明亮集体激发的有效能量重新归一致,并将其与纳米光子模式相结合。另一方面,我们表明,对于极端场合的情况,大型过渡偶极矩和低损失,完全包括直接偶极 - 偶极相互作用,对于正确捕获光学响应至关重要,许多集体状态都参与其中。为了量化此结果,我们提出了一个简单的方程式,该方程式指示直接相互作用强烈修改光学响应的条件。
信息网络资源的功能效率的间隔模型,用于生态专业知识的服务
摘要:本文考虑了信息Web资源的效率动力学的数学模型。在差异方程式的形式中,将间隔离散模型应用于证实,并提出了模型参数估计的方法。所提出的方法基于人工蜜蜂菌落算法(ABCA)。根据与环境监测服务相关的Web资源功能的数据进行了许多实验研究。已经研究了信息Web资源用户活动的指标。已考虑以差异方程为间隔模型(IDM)的三种模型构建案例。它们在一般的表达中有所不同。是计算实验的结果,这表明模型的充分性取决于差异方程的表达。在其错误选择的情况下,所提出的参数识别方法可能是有效的。描述了Web资源的效率的差异方程式中获得的间隔离散模型,使得在使用此Web资源的组织中优化业务流程以及最佳分配组织资源和行政服务中心员工的工作量成为可能。基于进行的实验,确定了所提出模型应用的效率。
使用卷积神经的手写方程求解器...
1个学生,2个学生,3个学生1计算机科学与工程,1 Sreenidhi科学技术研究所,印度城市摘要:由于技术进步,机器学习和深度学习变得越来越重要。手写识别,机器人技术,人工智能以及更多的行业现在正在使用机器学习和深度学习方法。这样的系统需要数据培训,使我们的机器可以学习并做出必要的预测。在这项研究中,证明了具有可观精度为98%的手写方程求解器。它是使用卷积神经网络和某些图像处理技术对手写数字和数学符号进行了训练的。数字0到9的图像,plus和sinus符号(+),手写符号 *构成数据集。为了提取功能,我们将使用轮廓提取。在此项目中,我们使用卷积神经网络构建模型,并训练该模型以评估手工编写的方程式,我们使用数字和操作员手工编写的数据集。给出了手写方程的输入图像,将图像转换为灰色背景,为此,我们使用轮廓提取来获取特征。输出是通过评估方程式
用于数学方程生成的表达式树解码策略
从自然语言生成数学方程式需要准确理解数学表达式之间的关系。现有的方法大致可分为标记级和表达式级生成。前者将方程式视为数学语言,顺序生成数学标记。表达式级方法逐一生成每个表达式。然而,每个表达式代表一个求解步骤,这些步骤之间自然存在并行或依赖关系,而现有的顺序方法却忽略了这些关系。因此,我们将树结构融入表达式级生成中,提倡表达式树解码策略。为了生成以表达式为节点的树,我们采用逐层并行解码策略:在每一层并行解码多个独立表达式(叶节点),并逐层重复并行解码,以顺序生成这些依赖于其他表达式的父节点表达式。此外,采用二分匹配算法将每一层的多个预测与注释对齐。实验表明,我们的方法优于其他基线方法,特别是对于那些具有复杂结构的方程。
1在超导体中,有两个关键特征...
II。 相干长度是对超导电子浓度在空间变化的磁场中无法发生巨大变化的距离的度量。 与伦敦方程是局部方程式不同,相干长度是对向量电位a(r)必须平均以获得J s(r)的范围的量度。 由于状态的空间变化需要额外的动能,因此有必要限制J S(R)的空间变化,以使额外的能量小于超导状态的能量差距。 比较平面波和调制波,获得相干长度的近似表达。II。相干长度是对超导电子浓度在空间变化的磁场中无法发生巨大变化的距离的度量。与伦敦方程是局部方程式不同,相干长度是对向量电位a(r)必须平均以获得J s(r)的范围的量度。由于状态的空间变化需要额外的动能,因此有必要限制J S(R)的空间变化,以使额外的能量小于超导状态的能量差距。比较平面波和调制波,获得相干长度的近似表达。
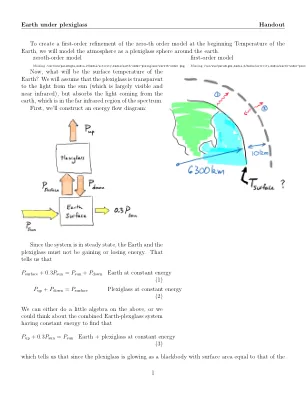
在有机玻璃讲义下的地球以创建一阶...
请注意,我们的有机玻璃温度的数学实际上与地球温度下的零级模型相同。,但现在我们正在解释现在数学的不同,因为这是地球表面的有机玻璃的温度。现在我们可以考虑有机玻璃的方程式。在这里,我们可以认识到p up = p向下,因为假设侧面在相同的温度下,各侧的有机玻璃会发出相同的速度。
NREL 的 REopt Lite 工具 - 开源
– 透明度 — 探索源代码以查找方程式和算法,这样您就可以准确地看到模型的工作原理。 – 灵活性 — 更改代码并构建您自己的 REopt Lite 版本以添加您的自定义功能和能力。 – 协作 — 贡献新模型、修复错误或与 NREL 合作实现可添加到 NREL 的 REopt Lite 产品的新功能。
人形机器人 Pyrène 的反应性步行
2 背景——实习开始时的最新水平 9 2.1 人形机器人行走:运动背后的方程式 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12 2.2 求解方程:控制方案的实施 . ... . . . . . . . . . . 19 2.3.1 通过控制发散运动分量进行接触扳手控制 20 2.3.2 全身导纳控制:CoM 策略 . . . . . . . . . . 21 2.4 实习目标 . . . . . . . . . . . . . . . 21 2.5 一般方法 . . . . . . . . . . . . . .... .... .... .... .... .... 22