XiaoMi-AI文件搜索系统
World File Search System时间演化
SU(2) 离散子群的原始量子门
格点规范理论 (LGT) 中量子效用的可能性非常大 [1 – 4] 。也许最重要的是，它为符号问题提供了一个优雅的解决方案，从而导致经典计算资源的指数级扩展 [5] ，从而无法在有限费米子密度和存在拓扑项的情况下进行大规模动力学模拟。为了研究这些基础物理主题，需要许多量子子程序。第一项任务是准备感兴趣的强耦合态，包括基态 [6 – 12] 、热态 [13 – 23] 和碰撞粒子 [24 – 34] 。对于动力学应用，时间演化算子 UðtÞ¼e−iHt 必须近似，并且存在许多不同的选择；特罗特化 [35,36]、随机编译 [37,38]、泰勒级数 [39]、量子比特化 [40]、量子行走 [41]、信号处理 [42]、幺正的线性组合 [38,43] 和变分方法 [44 – 47]，每种方法都有自己的权衡。除了状态准备和演化之外，重要的是需要开发有效的技术 [48 – 51] 和公式 [52 – 63] 来测量物理可观测量。为实现这一点，可以进一步使用算法改进，如误差缓解和校正
![arXiv:2104.08181v2 [quant-ph] 2021 年 11 月 25 日](/simg/e\e678bfa6a26a3bf97581ae01abe348a619519822.webp)
arXiv:2104.08181v2 [quant-ph] 2021 年 11 月 25 日
汉密尔顿量 H 的生成函数定义为 F ( t ) = ⟨ e − itH ⟩ ，其中 t 是时间，期望值取自给定的初始量子态。此函数可以访问不同阶数 K 的汉密尔顿量 ⟨ HK ⟩ 的不同矩。F ( t ) 的实部和虚部可以在量子计算机上分别使用一个额外的辅助量子位来评估，该辅助量子位对时间 t 的每个值都有一组测量值。量子比特的低成本使其在量子比特数量有限的近期非常有吸引力。假设可以使用量子设备精确计算生成函数，我们将展示如何在经典计算机上后验地使用此函数的信息内容来解决量子多体问题。说明了几种经典的后处理方法，旨在预测近似基态或激发态能量和/或近似长期演化。这种后处理可以使用基于 Krylov 空间的方法和/或与虚时间演化密切相关的 t 展开方法来实现。使用配对和费米-哈伯德模型在多体相互作用系统中说明了混合量子-经典计算。
减轻实际嘈杂中间体中的现实噪声...
量子误差缓解 (QEM) 对于嘈杂的中型量子 (NISQ) 设备至关重要。虽然大多数传统的 QEM 方案都假设离散门电路，噪声出现在每个门之前或之后，但这些假设不适合描述可能具有强门依赖性和复杂非局部效应的实际噪声，以及模拟量子模拟器等通用计算模型。为了应对这些挑战，我们首先扩展了场景，其中每个计算过程（无论是数字还是模拟）都由连续时间演化描述。对于来自工程汉密尔顿量缺陷或额外噪声算子的噪声，我们表明它可以通过随机 QEM 方法有效抑制。由于我们的方法仅假设精确的单量子位控制，因此它适用于所有数字量子计算机和各种模拟模拟器。同时，可以利用理查森外推法来抑制缓解过程中的错误。当我们在能量松弛和失相噪声下使用各种哈密顿量以及具有额外双量子比特串扰的数字量子电路对我们的方法进行数值测试时，我们发现模拟精度提高了 2 个数量级。我们评估了我们方案的资源成本，并得出结论，使用 NISQ 设备进行精确量子计算是可行的。
量子硬件上超紧哈密顿本征态的实时演化
在本文中，我们详细分析了变分量子相位估计 (VQPE)，这是一种基于实时演化的基态和激发态估计方法，可在近期硬件上实现。我们推导出该方法的理论基础，并证明它提供了迄今为止最紧凑的变分展开之一，可用于解决强关联汉密尔顿量。VQPE 的核心是一组具有简单几何解释的方程，它们为时间演化网格提供了条件，以便将特征态从时间演化的扩展状态集中分离出来，并将该方法与经典的滤波器对角化算法联系起来。此外，我们引入了所谓的 VQPE 的酉公式，其中需要测量的矩阵元素数量与扩展状态的数量成线性比例，并且我们提供了噪声影响的分析，这大大改善了之前的考虑。酉公式可以直接与迭代相位估计进行比较。我们的结果标志着 VQPE 是一种自然且高效的量子算法，可用于计算一般多体系统的基态和激发态。我们展示了用于横向场 Ising 模型的 VQPE 硬件实现。此外，我们在强相关性的典型示例（SVP 基组中的 Cr 2）上展示了其威力，并表明只需约 50 个时间步就可以达到化学精度。
JHEP01（2025）122
摘要：我们为证明弱宇宙审查制度猜想的量子版本而制定并迈出了两个大步。我们首先证明了“密码审查制度”：一个定理表明，当全息CFT的时间演化操作员在某些代码子空间上大约是伪数（或HAAR随机）时，相应的散装dual中必须有事件范围。此结果提供了一种一般条件，可以保证（在有限的时间）事件地平线形成，对全局时空结构的假设最少。我们的定理依赖于近期量子学习的扩展，而无需定理，并使用伪和测量浓度的新技术证明。将此结果应用于宇宙审查制度，我们将奇异性分开为古典，半普兰克和普朗克类型。我们说明经典和半普兰克奇异性与大约伪CFT时间演变兼容。因此，如果这种奇异性确实是伪造的，则通过加密审查制度，在没有事件范围的情况下它们就不可能存在。该结果提供了足够的条件，可以保证量子混乱和热化的精确全息结果（其一般适用性依赖于地平线的典型性）不会因ADS/CFT中的裸奇异性形成而无效。
患者特定的骨髓瘤疗法的纵向评估
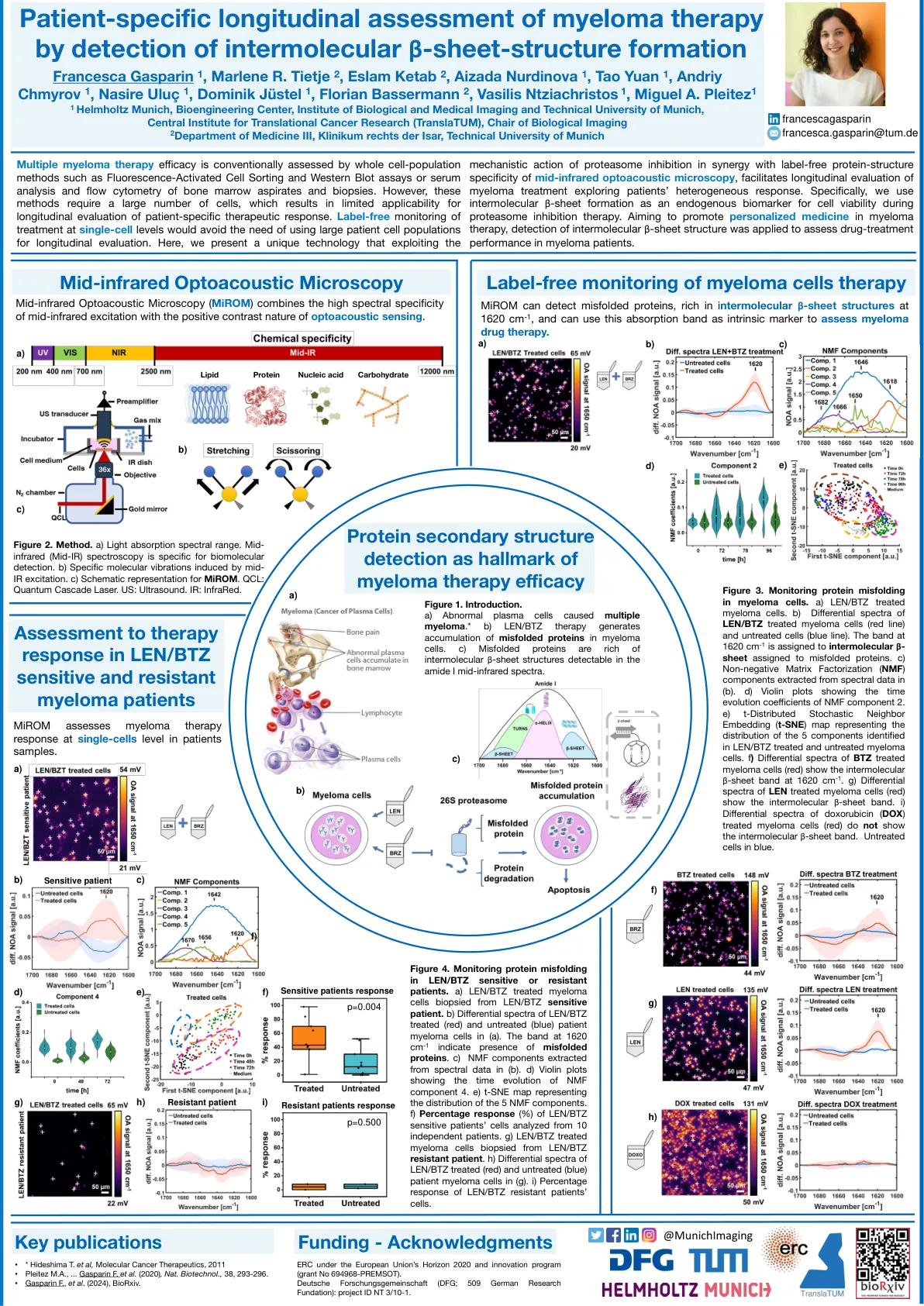
图3。监测骨髓瘤细胞中的蛋白质折叠率错折叠。a）LEN/BTZ治疗的骨髓瘤细胞。b）LEN/BTZ处理过的骨髓瘤细胞（红线）和未处理细胞（蓝线）的差异光谱。在1620 cm -1处的条带被分配给分子间分子β-分配给错误折叠蛋白的表。c）从（b）中的光谱数据中提取的非负矩阵分解（NMF）组件。d）小提琴图显示了NMF组分的时间演化系数2。E）T分布的随机邻居嵌入（T-SNE）图，代表了在LEN/BTZ处理过的5个成分和未经处理的骨髓瘤细胞中鉴定出的5个成分的分布。f）BTZ处理过的骨髓瘤细胞（红色）的差异光谱显示在1620 cm -1时分子间β-菜单带。g）LEN处理的骨髓瘤细胞（红色）的差异光谱显示了分子间β-片带。i）阿霉素（DOX）治疗的骨髓瘤细胞（红色）的差异光谱未显示分子间β-呈带。未处理的细胞为蓝色。
![arXiv:2207.01141v5 [quant-ph] 2023 年 4 月 14 日](/simg/8\8c8c25845fd86298065cd7ce5d12178a698e3819.webp)
arXiv:2207.01141v5 [quant-ph] 2023 年 4 月 14 日
在本研究中，我们首先收集并概括了几个现有的非微扰模型，用于描述任意弯曲时空中单个两级量子比特探测器与相对论量子标量场之间的相互作用，其中时间演化由简单生成的幺正体给出，即由施密特秩 1 相互作用哈密顿量生成的幺正体。然后，我们扩展了与这些非微扰模型相关的相对论量子通道，以包括量子场的非常大的一类高斯态，其中包括场上的相干和压缩操作（即高斯操作）的任意组合。我们表明，所有涉及非真空高斯态的物理结果都可以用与真空态相互作用的形式重新表述，但高斯算子通过伴随通道应用于场算子，从而有效地给出了时空中因果传播子形式的高斯运算的“傅里叶变换”解释。此外，我们表明，在这些非微扰模型中，可以精确计算 Rényi 熵，因此，通过复制技巧，可以计算与探测器相互作用后场态的冯·诺依曼熵，而无需对探测器和场的联合初始状态的纯度做出任何假设。这为我们提供了场的三参数“广义猫态”系列，其熵是有限的，并且精确可计算。
量子模拟的鸟类指南针的激进对动力学
n开放量子系统是与外部环境或浴室相互作用的量子系统。系统与浴室之间的相互作用通常太复杂，无法准确模拟，因此需要近似模拟才能平均浴室的效果，这导致了开放量子系统的非单身动力学。模拟量子系统的动力学一直是量子计算研究的主要重点，1-6但已经开发了相对较少的量子算法来模拟开放量子系统的动力学。7 - 16到这一目标，我们已经开发并展示了一种开放量子动力学17-19的通用量子算法，该算法能够模拟一般和复杂的物理系统。量子算法利用SZ.-NAGY单一扩张方法将非单身时间演化运算符转换为相应的单一操作员，然后可以在量子电路上实现。This quantum algorithm has been applied to a variety of physical systems, including the amplitude damping channel described by the Kraus representation, 17 the Jaynes − Cummings model described by the Kraus representation, 20 the Fenna − Matthews − Olson (FMO) complex described by the Lindblad master equation, 18 and the spin-boson model described by the generalized quantum master equation (GQME).19
通过在量子计算机上准备热状态来研究伊辛模型的临界行为
随着量子器件和量子算法的发展，量子计算机可以解决经典计算机难以解决的问题。量子计算机已经成功应用于量子化学、凝聚态物理和格子场论等许多领域（例如参见参考文献 [ 1 – 7 ]）。随着量子比特数量的增加和量子器件保真度的提高，我们可以处理更现实的物理模型，探索量子计算机的潜力。作为一个应用示例，本文用量子算法在不同温度下准备 Ising 模型的热态，包括接近临界温度和低温区域的点。为了证明我们方法的可行性，我们将所选物理量的量子模拟结果与经典模拟结果进行了比较。已经提出了许多算法来使量子计算机能够准备热态。这些方法包括量子热动力学方法，其中目标系统与处于平衡状态的溶液耦合 [8]；基于热场双态的变分量子算法 [9,10]；以及许多量子虚时间演化 (QITE) 算法，例如利用 Hubbard-Stratonovich 变换的算法 [11]、基于变分假设的 QITE (QITE-ansatz) [12]、基于测量的 QITE (QITE-measure) [13]，以及通过执行坐标优化的 QITE [14]。我们的研究范围集中在有噪声的中尺度量子 (NISQ) 设备的使用 [15,16]。考虑到量子
优化量子程序执行顺序以减少量子系统模拟中的错误
摘要 — 在量子力学细节层面模拟物理系统的时间演化——称为哈密顿模拟 (HS)——是物理学和化学领域一个重要而有趣的问题。对于这项任务，已知在量子计算机上运行的算法比传统算法快得多；事实上，这一应用促使费曼提出了量子计算机的构建。尽管如此，要达到这种性能潜力仍面临挑战。先前的工作重点是编译 HS 的电路（量子程序），目标是最大限度地提高准确性或门取消。我们的工作提出了一种同时推进这两个目标的编译策略。在高层次上，我们使用经典优化（例如图着色和旅行商）来排序量子程序的执行。具体而言，我们将哈密顿量（表征量子力学系统的矩阵）中相互交换的项组合在一起，以提高模拟的准确性。然后，我们重新排列每个组内的项，以最大限度地提高最终量子电路中的门取消。这些优化措施共同提高了 HS 性能，使电路深度平均减少了 40%。这项工作推动了 HS 的发展，进而推动了基础科学和应用科学领域的物理和化学建模。