XiaoMi-AI文件搜索系统
World File Search Systempatchnr:通过贴平归一化流正规化从极少数图像中学习
摘要 - 在无人驾驶汽车(UAV)上安装可重构的智能表面(RIS)有望改善传统的地面网络性能。与在无人机上部署被动性RIS的调用方法不同,这项研究探讨了空中活性RI(AARIS)的效率。特别是,研究了AARIS网络的下行链路传输,在此,基站(BS)利用速率分类的多个访问(RSMA)进行有效的干扰管理,并从AARIS支持AARIS的支持下,以共同扩大和反射BS的发射信号。考虑到有效RI的非琐碎能源消耗和无人机的能源储能有限,我们提出了一种创新的元素选择策略,以优化主动RIS元素的ON/OFF状态,该元素的ON/OFF状态可以自适应地管理系统的功耗。为此,提出了一个资源管理问题,旨在通过共同优化BS处的发射界限,元素激活,相移,相位移位和Active RIS的放大因子,用户的RSMA共同数据速率以及无人自由的RSMA共同数据速率,以及无人用的IAV的发电率来最大程度地提高系统能量效率(EE)。由于无人机和用户移动性的动态性质,深入的增强学习(DRL)算法设计用于资源分配,利用元学习来适应快速时变的系统动力学。根据模拟,整合元学习的系统EE会显着增加36%。此外,用AARIS代替固定的陆地活性RI会导致EE增强26%。
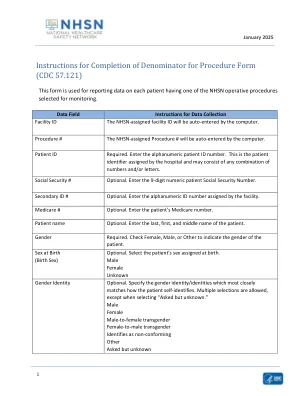
程序分母填写说明表(CDC 57.121)
选填。请指定患者是西班牙裔、拉丁裔,还是非西班牙裔或非拉丁裔;否则,选择“拒绝回应” 未知注意:在患者无法交流和/或无法获取此信息的极少数情况下,请选择“未知”。 种族 选填。请指定以下一个或多个选项来确定患者的种族: 美洲印第安人或阿拉斯加原住民(1002-5) 亚裔(2028-9) 黑人或非裔美国人(2054-5) 中东或北非(2118-8) 夏威夷原住民或其他太平洋岛民(2076-8) 白种人(2106-3) 拒绝回应 未知注意:在患者无法交流和/或无法获取此信息的极少数情况下,请选择“未知”。 语言 选填。从 NHSN 简略主要语言列表中指定患者的首选语言,该列表可在以下网址获得: https://www.cdc.gov/nhsn/pdfs/NHSN-Abridged-Primary-Language- List.xlsx 。 拒绝回应 未知 注意:在患者无法交流和/或无法获取此信息的极少数情况下,选择“未知”。 是否需要翻译?选填。如果需要翻译以患者的首选语言与其交流,请选择“是”;否则,选择“否”。 拒绝回应 未知 注意:在患者无法交流和/或无法获取此信息的极少数情况下,选择“未知”。 事件类型 必填。输入程序代码 (PROC)。
2019冠状病毒病疫苗
请注意,有经过培训的医务人员随时为您解答疑问。在极少数情况下,如果出现不良过敏反应,在观察区,医务人员可以使用所有适当的设备和用品,并能够采取适当的措施确保您的安全。
COVID-19 疫苗的副作用
与所有疫苗一样,接种 COVID-19 疫苗后可能会出现极少数过敏反应。如果您在接种疫苗后或注射药物后立即出现严重过敏反应,则应在接种 COVID-19 疫苗前联系医生。
过敏和 COVID-19 疫苗接种
我们想为您提供一些有关过敏和 COVID-19 疫苗接种的信息。正如您可能从媒体上了解到的那样,在接种 Biontech/Pfizer 和 Moderna 的两种目前可用的 mRNA COVlD-19 疫苗后不久,在极少数情况下会出现严重的全身反应。因此,英国卫生当局发布了一项临时建议,将“严重过敏”或“过敏反应”患者排除在疫苗接种之外。这在国际上以及德国都导致了含糊其辞。原则上,每次接种疫苗(不仅仅是针对 COVID-19 的疫苗)时,在极少数情况下(每 100,000 至 100 万次接种中 1 例)都可能发生过敏或过敏反应。这可能是由于疫苗本身或疫苗中的佐剂/添加剂造成的。对于患有以下过敏/特应性疾病的患者,没有证据表明接种经批准的疫苗会增加风险(与正常人群相比):
从转移性癌症幸存者到马拉松运动员
教育创新奖旨在表彰一个人,或者在极少数情况下是两人团队,因为它开发了一种直接改善医学或生物医学教育的资源。该奖项旨在鼓励教师创造性地运用自己的才能,以提高学习者的学术需求
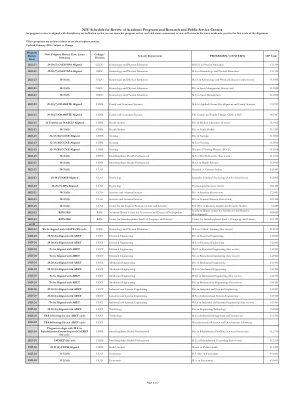
NIU 学术课程和研究及公共服务中心审查时间表 由于课程审查与学科认证周期相一致
NIU 学术课程和研究及公共服务中心审查时间表由于课程审查与学科认证周期相一致,因此在极少数情况下,课程审查和中期状态评估审查将在协调的第一个周期的同一学年进行。