XiaoMi-AI文件搜索系统
World File Search System使用潜在向量表示的晶圆图缺陷模式半监督分类
摘要 —随着半导体设计和制造工艺的全球化,集成电路制造阶段的缺陷检测需求变得越来越重要,在提高半导体产品的产量方面发挥着重要作用。传统的晶圆图缺陷模式检测方法涉及使用电子显微镜进行手动检查以收集样本图像,然后由专家评估缺陷。这种方法劳动密集且效率低下。因此,迫切需要开发一种能够自动检测缺陷的模型来替代手动操作。在本文中,我们提出了一种方法,该方法首先采用预先训练的 VAE 模型来获取晶圆图的故障分布信息。该信息作为指导,结合原始图像集进行半监督模型训练。在半监督训练期间,我们利用师生网络进行迭代学习。本文提出的模型在基准数据集 WM-811K 晶圆数据集上进行了验证。实验结果表明,与最先进的模型相比,该模型具有更高的分类精度和检测性能,满足了工业应用的要求。与原始架构相比,我们取得了显着的性能提升。索引术语——缺陷检测;半监督学习;无监督学习;变异自动编码器
CANFDWIFI-100U 用户手册
5.1 硬件连接 ................................................................................................................. 10 5.2 软件安装 ................................................................................................................. 10 5.3 配置设备 ................................................................................................................. 10 5.3.1 打开配置工具 ................................................................................................. 11 5.3.2 搜索设备 ......................................................................................................... 12 5.3.3 配置参数 ......................................................................................................... 13 5.4 CANFDWIFI-100U 与 USBCANFD-200U 通信 .................................................. 15 5.5 无线连接模式 ......................................................................................................... 23 5.5.1 AP 热点模式 ................................................................................................... 23 5.5.2 Station 客户端模式 ......................................................................................... 24 5.6 工作模式使用说明 ................................................................................................. 25 5.6.1 TCP Server 模式 ............................................................................................. 26 5.6.2 TCP Client 模式 .............................................................................................. 27 5.6.3 UDP 模式 ........................................................................................................ 28 6.其他功能说明 ......................................................................................................... 30
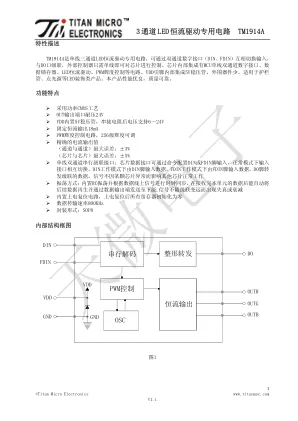
3通道LED恒流驱动专用电路TM1914A
功能说明 1、模式设置 本芯片为单线双通道通讯,采用归一码的方式发送信号。芯片接收显示数据前需要配置正确的工作 模式,选择接收显示数据的方式。模式设置命令共48bit,其中前24bit为命令码,后24bit为检验反码, 芯片复位开始接收数据,模式设置命令共有如下3种: (1)0xFFFFFF_000000命令: 芯片配置为正常工作模式。在此模式下,首次默认DIN接收显示数据,芯片检测到该端口有信号输 入则一直保持该端口接收,如果超过300ms未接收到数据,则切换到FDIN接收显示数据,芯片检测到该 端口有信号输入则一直保持该端口接收,如果超过300ms未接收到数据,则再次切换到DIN接收显示数据。 DIN和FDIN依此循环切换,接收显示数据。 (2)0xFFFFFA_000005命令: 芯片配置为DIN工作模式。在此模式下,芯片只接收DIN端输入的显示数据,FDIN端数据无效。 (3)0xFFFFF5_00000A命令: 芯片配置为FDIN工作模式。在此模式下,芯片只接收FDIN端输入的显示数据,DIN端数据无效。 2、显示数据
多通道人机交互信息融合的智能方法
结构在运行时可以做到即使某一个模态信息缺失整个网络也能取得不错的效果 , 在多通道情感识别、 语义理解、目标学习等领域取得很好的效果 .尽管如此 , 这类网络相对于任务来说还是相对 “ 具体 ”, 如 果要换一个任务 , 用户就需要修改网络结构包括重新调整参数 , 这使得深度神经网络结构的设计是一 个耗时耗力的过程 .因此研究者们希望一个混合的神经网络结构可以同时胜任多个任务 , 以减少其在 结构设计和训练方面的工作量 .鉴于此 , 研究者开始致力于首先采用大数据联合训练构建出多通道联 合特征分享层 , 然后在识别阶段可以同时进行多任务处理的深度多模态融合结构 .如 Google 的学者 尝试建议一个统一的深度学习模型来自适应地适配解决不同领域、不同数据模态下的多个不同类型 的任务 , 且在特定任务上的性能没有明显损失的模型 [71] .该模型构架请见文献 [71] 的图 2, 由处理输 入的编码器、编码输入与输出混合的混合器、混合输出的解码器 3 个部分构成 , 文献 [71] 的图 3 给 出了这 3 个部分的详细描述 .每一个部分的主体结构类似 , 均包含多个卷积层、注意力机制和稀疏门 控专家混合层 .其中 , 不同模块中的卷积层的作用是发现局部模式 , 然后将它泛化到整个空间 ; 注意力 模块和传统的注意力机制的主要区别是定时信号 , 定时信号的加入能让基于内容的注意力基于所处的 位置来进行归纳和集中 ; 最后的稀疏阵列混合专家层 , 由前馈神经网络 ( 专家 ) 和可训练的门控网络组 成 , 其选择稀疏专家组合处理和鉴别每个输入 .
对应图图的随机光谱采样
3D对应关系,即一对3D点,是计算机视觉中的一个有趣概念。配备兼容性边缘时,一组3D相互作用形成对应图。此图是几个最新的3D点云注册方法中的关键集合,例如,基于最大集团(MAC)的一个。但是,其特性尚未得到很好的理解。因此,我们提出了第一项研究,该研究将图形信号处理引入了对应图图的域。我们在对应图上利用了广义度信号,并追求保留此信号的高频组件的采样策略。为了解决确定性抽样中耗时的奇异价值分解,我们采取了随机近似采样策略。因此,我们方法的核心是对应图的随机光谱采样。作为应用程序,我们构建了一种称为FastMAC的完整的3D注册算法,该算法达到了实时速度,而导致性能几乎没有下降。通过广泛的实验,我们验证了FastMac是否适用于室内和室外基准。例如,FastMac可以在保持高recistra-
沙子图与弦弦图制作
很长一段时间以来,土著社会被排除在数学史领域(D'Ambrosio,1985,2001)。直到几十年前,科学的历史学家和哲学家确实抛弃了他们的研究领域,经常赋予口头传统的小规模和/或土著社会。The prevalence of the evolutionist (Tylor, 1871) and “prelogical thought” (Lévy-Bruhl, 1910) theories, arguing that these peoples had a lesser ability to abstract and generalize than ours, appears to have durably impeded the recognition of genuine mathematical practices carried out in the various indigenous societies worldwide (Vandendriessche,即将到来的2021)。在20世纪下半叶初,在这个问题上发生了重大的认识论变化,这是通过人类学家克劳德·莱维·斯特劳斯(ClaudeLévi-Strauss)的工作促进的。后者的认识论破裂似乎促使研究(在1970年代)的发展现在通常被认为是建立民族心理学的开创性作品(Vandendriessche&Petit,2017年)。这个新生的跨学科研究领域的当前发展有助于进一步扩大我们对数学知识及其历史的看法,同时在图片中包括所有在社会群体/社会中表现出的数学特征的所有活动,通常不被认为是这样的。在地球的各个土著社会中,数学并不是通常作为自治知识类别。(Rivers&Haddon 1902,Deacon&Wedgwood,1934年,Austern 1939,Lévi-Strauss 1947,Pinxten等人。然而,正如许多关于“传统”社会的民族志都表明,在整个20世纪,在其各种实践中(例如日历或装饰品的制作,营地和住宅的建立,纺织品生产,导航,接航,游戏,游戏,游戏,游戏,1983,Gladwin 1986,Mackenzie 1991,Desrosiers,2012,Galliot 2015…)。因此,eTnomecatians的一个主要认识论问题是确定其中一些实践与数学活动以及如何相关的程度。为了避免受到“数学一词的西方涵义”的约束,玛西娅·阿什尔(Marcia Ascher,1935-2013)是1990年代民族心理学的创始人之一,引入了“数学思想”的概念。数学思想被定义为涉及“数字,逻辑和空间配置,尤其是这些思想在系统或结构中的布置”的想法(Ascher,1991:3)。Ascher基于使用建模工具的使用开发了一种方法,旨在揭示与
图的量子态
1 代数结构与应用研究组,阿卜杜勒阿齐兹国王大学科学与艺术学院数学系,拉比格 21911,沙特阿拉伯;abdulnadimkhan@gmail.com 2 代数结构与应用研究组,阿卜杜勒阿齐兹国王大学科学学院数学系,吉达 21589,沙特阿拉伯;analahmadi@kau.edu.sa (ANA);whbasaffar@kau.edu.sa (WB);jwph@sussex.ac.uk (JWPH);hashoaib@kau.edu.sa (HS) 3 弗林德斯大学科学与工程学院,阿德莱德,SA 5001,澳大利亚; david.glynn@flinders.edu.au 4 Dhirubhai Ambani 信息与通信技术研究所,Gandhinagar 382007,古吉拉特邦,印度;mankg@computer.org 5 I2M,(法国国立科学研究院,艾克斯-马赛大学,马赛中央理工学院),163 Avenue de Luminy,13009 马赛,法国 * 通讯地址:arifraza03@gmail.com(MAR);patrick.sole@telecom-paris.fr(PS)