XiaoMi-AI文件搜索系统
World File Search System复杂模糊粗糙弗兰克聚集算子概念下的土木工程人工智能工具分类
近来,研究人员试图处理最多的信息,并使用那些不会丢失数据或信息丢失最少的技术和方法。模糊集和复杂模糊集等结构无法讨论上近似值和下近似值。此外,我们可以观察到模糊粗糙集无法讨论第二维,在这种情况下,可能会丢失数据。为了涵盖以前想法中的所有这些问题,笛卡尔形式的复杂模糊粗糙集概念是当今的需求,因为这种结构可以讨论第二维以及上近似值和下近似值。为此,在本文中,我们开发了笛卡尔形式的复杂模糊关系和复杂模糊粗糙集理论。此外,我们基于弗兰克 t 范数和 t 范数提出了复杂模糊粗糙数的基本定律。可以将整体输入转换为单个输出的基本工具称为聚合运算符 (AO)。因此,基于 AO 的特征,我们定义了复杂模糊粗糙 Frank 平均值和复杂模糊粗糙 Frank 几何 AO 的概念。利用已开发的理论来展示所提供方法的重要性和有效性是必要的。因此,基于已开发的概念,我们为此目的定义了一种算法以及一个说明性示例。我们利用引入的结构对土木工程 AI 工具进行分类。此外,对所提供方法的比较分析表明,与现有概念相比,引入的结构有所进步。
人工智能教科书
1.1.日常生活中的人工智能例证 1 1.2.未来人工智能 8 2.1。工业革命 4.0 12 2.2.电话银行 14 2.3.工业革命的时代发展 15 3.1.图灵机 19 3.2.图灵机演示 21 3.3.图灵机 22 3.4。图灵机可视化 23 3.5.图灵机转换图 26 4.1.机器学习 29 4.2.黑箱数据处理 32 4.3. Alpha Go 33 4.4。机器学习 34 5.1.深度神经网络 36 5.2.神经元如何工作 37 5.3.神经元数学方程 37 5.4.线性激活函数 38 5.5. Sigmoid 和 Tanh(非线性) 39 5.6。整流线性 39 5.7。具有隐藏层的神经网络架构 40 5.8.具有 2 个隐藏层的神经网络架构 40 6.1。 Matlab 45 7.1。模糊推理系统 52 7.2。清晰集图 54 7.3.模糊集图 55 7.4。脆皮逻辑 56 7.5。模糊逻辑 56 7.5。脆皮逻辑 56 7.6。酥脆套餐 58 7.7.模糊集 59 7.8。三角隶属函数 59 7.9.梯形隶属度 60 7.10 与集合隶属度相关的模糊值。 61 7.11。 1 型模糊逻辑系统结构 63
教授Amlan Chakrabarti 博士简历
具有增强词语表示的编码器架构,载于 Springer Applied Intelligence,2022 年。4. S. Sarkar、DP Mukherjee 和 A. Chakrabarti,“强化学习用于足球传球检测和控球统计数据生成”,载于 IEEE Transactions on Cognitive and Developmental Systems,2022 年,doi:10.1109/TCDS.2022.3194103。 5. M. Rakshit、S. Bhattacharjee、G. Garai、A Chakrabarti,“正交频分复用系统中基于音调预留的峰值与平均功率比降低技术的新型差分进化算法”,Swarm and Evolutionary Computation,爱思唯尔,第 72 卷,2022 年 7 月 6. A. Saha、R. Majumdar、D. Saha、A. Chakrabarti 和 S. Sur-Kolay,“具有 n-qudit Toffoli 门高级分解的 d-ary Grover 算法的渐近改进电路”,Phys. Rev. A,第 72 卷。 105,062453 – 2022 年 6 月 28 日发布。7. AK Das、B Chakraborty、S Goswami、A Chakrabarti,“一种基于模糊集的有效特征选择方法”,模糊集与系统,爱思唯尔,印刷中,2022 年。8. T. Chatterjee、A. Das、SI Mohtashim、A. Saha、A. Chakrabarti,“Qurzon:基于分而治之的分布式量子系统量子编译器原型”,Springer Nature Computer. Science,第 3 卷,323,2022 年。9. S. Basu、A. Saha、A. Chakrabarti 和 S. Sur-Kolay,“i-QER:一种减少量子误差的智能方法”,ACM Transactions on Quantum Computing,已接受(2022 年 5 月)。
基于机器学习的结直肠癌患者的影响
人工智能(AI)在教育中的影响可以看作是一个多属性的小组决策(MAGDM)问题,其中一些利益相关者根据不同的偏好和标准评估AI应用程序在教育环境中的优势和缺点。MAGDM框架可以通过有条不紊地分析包括道德,社会,教学和技术问题在内的许多组成部分中的交易和冲突来帮助提供透明且合乎逻辑的建议来实施教育中的AI。模糊集理论中的一种新颖的发展是2-元组语言Q -Rung Orthopair模糊集(2TL Q -ROFS),它不仅是一种广义形式,而且还可以整合决策者的定量评估思想和定性评估信息。2TL Q -ROF Schweizer -Sklar加权平均功率平均操作员(2TL Q -ROFSSWPA)和2TL Q -ROF Schweizer -Sklar加权几何(2TL Q -ROFSSWPG)操作员是我们在本文中创建的两个聚合操作员。我们还研究了拟议运营商的一些独特实例和特征。接下来,基于2TL Q -ROF构建了一个新的熵模型,该模型可能利用决策者的偏好以获得属性的理想客观权重。接下来,我们将Visekriterijumska Optimizacija I Kompromisno Resenje(Vikor)技术扩展到2TL Q -ROF版本,该版本为决策者提供了更大的空间来代表他们的决策,同时还考虑了人类认知中固有的不确定性。进行了比较研究以检查开发方法的好处和改善。最后,一个案例研究,讲述了人工智能如何影响教育以显示既定方法的适用性和价值。
基于量子态判别的多类分类
我们提出了一个通用框架,用于解决多类分类问题,该框架使用可以解释为模糊集的分类函数。我们在基于量子态鉴别技术的量子启发式分类器领域专门研究这些函数。具体来说,我们使用由给定数据集的训练集确定的模糊可观测量(正算子值测度)来构建这些分类函数。我们表明,一旦这些分类函数从训练数据集的量子编码中“提炼”(在经典平台上),就可以在近期的量子计算机上测试此类分类器。我们将这些实验结果与理论结果进行了比较,并提出了一些问题以供未来研究。© 2023 Elsevier BV 保留所有权利。
fuzz-ieee 2025 SS:模糊机器学习
呼吁论文:传统的机器学习模型缺乏处理现实世界不确定性,提供可解释模型的能力,并提供了支持动态环境的强大机制。模糊集,模糊逻辑和模糊系统以其对不确定性建模的能力,增强模型的可解释性的能力而闻名,并提供了一种有效且灵活的方式来表示数据和导航预测模型。因此,机器学习和模糊技术的整合是盛行的,并且在许多领域都取得了巨大的成功。这个特别会议旨在为研究人员提供一个论坛,以分享整合模糊技术和机器学习方法的最新结果。
环境规制手段对农业企业技术创新的影响——基于fsQCA的配置效应研究
本文采用模糊集定性比较分析法(fsQCA)研究了各类环境规制工具(ERI)与农业企业技术创新之间的复杂因果关系。研究发现,一套设计良好的ERI可以促进农业企业的技术创新;控制指令型ERI不能单独促进农业企业的技术创新,市场激励型ERI对促进企业创新绩效必不可少,隐性ERI在促进企业创新方面发挥着重要作用,自愿性ERI在促进企业技术创新方面的作用不显著。政府应协调不同类型的ERI,改进ERI的设计,以实现农业部门经济和环境绩效的双赢。
量子退火器上的模糊逻辑 - NTU > IRep
摘要 — 量子计算将通过利用叠加、纠缠和干涉等量子力学效应,实现大规模并行算法的设计,从而以有效方式解决难题,从而彻底改变计算领域。这些计算改进可能会对模糊系统在诸如大数据等环境中的设计和使用方式产生重大影响,在这些环境中,计算效率是一个不可忽略的约束。为了为这一创新方案铺平道路,本文介绍了一种基于二次无约束二元优化 (QUBO) 问题的模糊集和运算符的新表示,以便在一种称为量子退火器的量子计算机上实现模糊推理引擎。
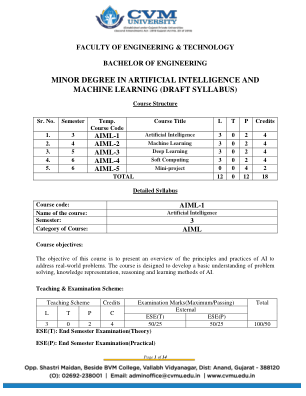
人工智能辅修学位和
1. 学习 MATLAB 或 Scilab 中的模糊逻辑工具箱。2. 使用 Matlab 为给定应用设计模糊集。3. 设计用于机器人运动的模糊控制系统。4. 感知器学习算法的实现。5. 学习 MATLAB 或 Scilab 中的神经网络工具箱。6. 使用神经网络进行 IRIS 数据分类。7. 将神经网络应用于回归数据集。8. 学习 MATLAB 中的模式识别工具。9. 学习 MABLAB 或 Scilab 中的遗传算法工具箱。10. 为给定的优化问题实现/使用遗传算法 11. 使用遗传算法进行参数调整。12. 使用神经网络或 GA 或模糊逻辑实现任何项目。
JB HI 特别专题“脑信号和神经成像的模糊系统和计算方法:
鉴于处理从神经成像模式获得的脑信号所面临的重大挑战,模糊集和系统已被提出作为分析脑活动的有用且有效的框架,以及实现脑与外部设备(脑机/机接口)之间的直接通信途径。虽然人们对这些问题的兴趣越来越大,但模糊系统的贡献因应用领域而异。一方面,考虑到脑活动的解码,处理不确定性的高级计算智能方法(如模糊集和系统)代表了一种极好的工具,可以克服处理极度嘈杂的信号的挑战,这些信号很可能受到非平稳性、不变量和泛化能力差的影响。另一方面,就神经科学研究而言,可能性和模糊性同样被用于测量突触、神经元和大脑区域或区域之间的平滑整合。在此背景下,拟议的特刊旨在建立一个专门的论坛,作为计算智能研究人员的媒介,他们希望利用模糊系统和模糊逻辑等先进技术来模拟和表达对脑信号和神经成像数据分析的不确定性。任何与神经科学相关的领域,如计算神经科学、脑机接口、神经科学、神经信息学、神经人体工程学、计算认知神经科学、情感神经科学、神经生物学、脑映射、神经工程和神经技术都是合适的。本期特刊重点介绍在不同知识领域研究的模糊系统和应用于脑信号和神经成像的计算方法的最新进展、挑战和未来前景。因此,我们邀请研究人员为本期特刊贡献原创作品,利用脑信号和神经成像中使用计算和数学技术的最新方法,并解决开发用于各种临床应用的专用系统的挑战,同时提出未来发展的新想法和方向。感兴趣的主题包括但不限于以下内容: