XiaoMi-AI文件搜索系统
World File Search SystemDPD法100次
(7)其他 a.须在投标开始前提交《资格审查结果通知书》副本。若您已经提交过,则无需再次提交。 若申请人由代表人或其他代理人代为竞投,则其须于竞投开始前提交《授权委托书》。 邮寄投标应清楚写明公司名称、投标日期和时间、投标主题,并用红色写明“投标附件”,并于6月21日星期五中午12点之前邮寄到下述地址。此外,投标人还将提前通过邮件收到投标意向通知。 如果您希望参与竞标,您必须在 6 月 19 日星期三中午 12:00 之前通过电话联系我们并提交市场价格调查。 投标同等产品时,其标准必须等于或高于标准栏所示的标准或规格。 该产品必须被视为等效产品,并必须在 6 月 19 日星期三下午 5:00 之前向合同官员提交“等效性判定请求”以获得批准。 投标者在参与前必须同意《驻军使用标准合同》和《投标及合同指南》(在东部陆军会计司令部网站(https://www.easternarmy.gov/accountingcommand/eae/kaikei/eafin/index.html)或在泷原驻军会计司令部办公室公布)。 (k)通过提交投标文件,您将被视为已经按照“关于排除有组织犯罪集团的承诺”作出承诺。投标文件中应当包含下列声明作为接受的表示: “本公司(本人(若为个人)、本公司(若为团体))谨此承诺本誓约书所列事项,以排除有组织犯罪为目的。” 此外,拒绝提交上述“排除有组织犯罪承诺事项”的誓约书的,将无法参与投标。 Q 如果有投标人在首次投标时通过邮寄方式提交了投标,则重新投标的时间如下。
外国国家豁免法DISCLAIMER
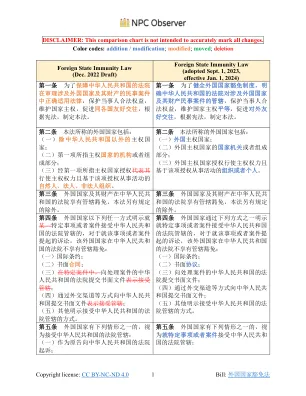
第十二条 外国国家与包括中华人民共和 国在内的其他国家的 组织或者个人 之间的 商业活动产生的争议,根据书面协议被提 交仲裁的,或者外国国家通过国际投资条 约等书面形式同意将其与包括中华人民共 和国在内的其他国家的 组织或者个人 产生 的投资争端提交仲裁的, 对于需要法院审 查的下列事项 ,该外国国家在中华人民共 和国的法院不享有管辖豁免: (一)仲裁协议的效力; (二)仲裁裁决的承认 和执行 ; (三)仲裁裁决的撤销; (四)法律规定的其他 由中华人民共和国 的法院 对仲裁进行审查的事项。 第十三条 外国国家的财产享有司法强制 措施豁免,但有下列情形之一的除外: (一)外国国家以国际条约、 仲裁协议、 书面合同 或者向中华人民共和国的法院提 交书面文件的方式明示放弃司法强制措施 豁免; (二)外国国家已经拨出或者专门指定财 产用于司法强制措施执行的; (三)为执行中华人民共和国的法院的生 效判决,且外国国家的财产用于商业活 动、与诉讼有联系、位于中华人民共和国 领域内的。 外国国家接受中华人民共和国的法院管 辖,不应视为放弃司法强制措施豁免。
《香港国安法》法律论坛
两年前的今天,全国人大作出《 528 决定》,授权全国人大常委 会制定《香港国安法》。全国人大常委会其后在 6 月 30 日通过《香港 国安法》,并列入《基本法》附件三,在香港特区公布实施。当天晚 上,我以香港特区行政长官身分签署政府公告,让《香港国安法》 在香港实施,深感责任重大,使命光荣。由于当时香港正经历了 差不多一年的暴力冲击、社会动乱,国家安全受到威胁,人命财产 得不到保障,《香港国安法》的颁布实施无疑是香港的「定海神针」。
左旋DNA WiSE 左旋DNA 左旋酶世界绿色基因法医侦探法医...
冷泉港实验室DNA学习中心(DNALC)是世界上第一个完全致力于关系教育的科学中心。超过30,000名学生参加了我们的科学营。在老师丰富的指导下,升6至12年级的学生使用先进的实验设备和电脑设备进行了同侪好几个年级的实验。
多孔陶瓷材料力学特性的离散单元法定量模拟
引用格式 : 周爽 , 苏景林 , 刘晓星 , 等 .多孔陶瓷材料力学特性的离散单元法定量模拟 .中国科学 : 物理学力学天文学 , 2019, 49: 064602 Zhou S, Su J L, Liu X X, et al.Quantitative simulation of mechanical properties of porous ceramic materials by discrete element method (in Chinese).Sci Sin-Phys Mech Astron, 2019, 49: 064602, doi: 10.1360/SSPMA2018-00332
电子导航研究所
全球 ATM 运行概念是由国际民航组织制定的,目的是在适应日益增长的交通量的同时,实现安全、可持续和环保的空中交通运行。ENRI 公布了其长期研究愿景,并一直致力于研究,以及为实现全球 ATM 运行概念 (GATMOC) 而在全球范围内开发和传播成果。长期研究愿景需要根据社会环境的变化和新开发技术的引入进行审查。因此,ENRI 定期审查其长期研究愿景,考虑与 CARATS * 和 GANP ** 等其他空中交通系统长期愿景的协调,并于 2019 年发布了最新版本。未来将实现基于轨迹的运行 (TBO),其中飞机轨迹会提前调整和确定,飞机将在指定时间沿着轨迹飞行。灵活的空中交通管理对于应对各种类型、不同性能和用途的飞机的预期增长至关重要。新的研究愿景将我们未来几十年的研究主题解释为路线图,其中主题大致分为四个研究领域:“通过提高运营安全性和可靠性有效利用空域”、“通过空域运营效率有效利用空域”、“优化机场运营”和“改善空中交通系统的基础技术”,重点是提高研究潜力并持续长期为社会做出贡献。ENRI 将根据这一长期愿景开展其研究和开发活动。
SEGGER 宣布支持意法半导体的STM32C0 MCU 系列
SEGGER 的高性能实时操作系统 embOS-Ultra 也已支持 STM32C0 系列。它使用循环分辨率计 时,提供更高的精度和时间分辨率。使用 embOS-Ultra 可提高性能并节省功耗,它还为应用 程序提供了可同时使用基于周期和基于微秒的计时选项。 API 与 embOS 完全兼容,使迁移变 得简单,无需更改应用程序,并保持 embOS 行为。 embOS-Ultra 只是在使用新的附加 API 调 用时提供循环计时,不用在两者之间做出选择。了解 embOS-Ultra ,可以点击文章: embOS- Ultra :高分辨率系统时间
电子导航研究所 - 电子航法研究所
全球 ATM 运行概念是由国际民航组织制定的,旨在实现安全、可持续和环保的空中交通运行,同时适应不断增加的交通量。ENRI 公布了其长期研究愿景,并一直致力于研究,以及在全球范围内开发和传播成果,以实现全球 ATM 运行概念 (GATMOC)。长期研究愿景需要根据社会环境的变化和新开发技术的引入进行审查。因此,ENRI 定期审查其长期研究愿景,考虑与 CARATS * 和 GANP ** 等其他空中交通系统长期愿景的协调,并于 2019 年发布了最新版本。未来将实现基于轨迹的运行 (TBO),其中飞机轨迹会提前调整和确定,飞机将在指定时间沿轨迹飞行。灵活的空中交通管理对于应对具有不同性能和用途的各种类型飞机的预期增加至关重要。新的研究愿景将未来几十年的研究课题以路线图的形式阐述,其中研究课题大致分为四个研究领域:“通过提高运行安全性和可靠性有效利用空域”、“通过空域运行效率有效利用空域”、“优化机场运营”和“改善空中交通系统的基础技术”,重点是提高研究潜力并持续长期为社会做出贡献。ENRI 将根据这一长期愿景开展研究和开发活动。