XiaoMi-AI文件搜索系统
World File Search System滴眼剂
处理和使用过程中的安全规范...
• 按照制造商的指导方针，使用适量的水来稀释滴眼或滴鼻疫苗。 • 向每只鸡的眼睛或鼻孔中滴入一滴疫苗。 • 使用塑料滴管将疫苗滴入鸡的鼻子或眼睛中。 • 将疫苗滴入眼睛或鼻孔后，握住鸡的喙，直到观察到鸡的吞咽动作。 • 将滴管瓶倒置，保持垂直位置，以确保正确的液滴大小并避免疫苗丢失。 • 如果疫苗滴液溢出眼睛或鼻孔外，请立即重新注射疫苗。
免疫史证明
必需的免疫接种 两剂 MMR 疫苗或 MMR 滴度 (IgG) 证明对这 3 种疾病均有免疫力 – 必须提供证明 *活病毒疫苗 (MMR) 会影响结核菌素皮肤试验 (TST/PPD) 的准确性；请在接种 MMR 疫苗的同时或之前完成至少一剂 TST。 __________ __________ 或 __________________________________ 麻疹 第 1 剂 第 2 剂 麻疹滴度的日期和结果（提供阳性/免疫 IgG 的副本） __________ __________ 或 __________________________________ 腮腺炎 第 1 剂 第 2 剂 腮腺炎滴度的日期和结果（提供阳性/免疫 IgG 的副本） __________ 或 __________________________________ 风疹 第 1 剂 风疹滴度的日期和结果（提供阳性/免疫 IgG 的副本）
分布式量子交互式证明 - 滴
在本文中，我们介绍了分布式交互式证明的量子对应物：现在可以是量子位，网络的节点可以执行量子计算。本文的第一个结果表明，通过使用分布式量子交互式证明，可以大大减少相互作用的数量。更确切地说，我们的结果表明，对于任何常数K，可以由k-turn classical（即非量词）分布式交互式协议决定的语言类别，具有F（n）-bit证书大小中包含的语言中包含，可以由5-Turn分布式量子交互协议与O（f（f（f（f））），可以决定使用5-Turn分布式交互协议。我们还表明，如果我们允许使用共享的随机性，则可以将转弯数减少到三个。由于目前尚无类似的转向还原经典技术，因此我们的结果也证明了在分布式交互式证明的设置中量子计算的力量。
量子电路的有效分布 - 滴
量子计算硬件的鲁棒性正在改善，但是单个计算机仍然具有少量的Qubits（用于存储量子信息）。需要大量Qubits的计算只能通过在较小的量子计算机网络上分配来执行。在本文中，我们考虑了在量子计算机的均匀网络上分发量子计算的问题，以量子电路表示，从而最小化完成计算的每个步骤所需的通信操作数量。我们提出了一个两步解决方案：将给定电路的Qubit在网络中的计算机之间进行，并调度通信操作（称为迁移），以在计算机之间共享量子信息，以确保每个操作都可以在本地执行。虽然第一步是一个棘手的问题，但我们在特殊设置中为第二步提供了多项式时间解决方案，在一般环境中提出了O（log n） - 值得称的解决方案。我们提供的经验结果表明，我们的两步解决方案的表现优于该问题的现有启发式效果（在某些情况下，最高90％）。
银河令牌滑动 - 滴
给定图G和两个独立的集合i和大小为K的I T，独立集合构造问题询问是否存在一系列独立集（k）i s = i 0，i 1，i 2，。。。，iℓ= i t，使每个独立集都使用所谓的重新配置步骤从上一个独立集获得。将每个独立的集合视为放置在图G的顶点上的K代币集合，研究的两个重新配置步骤是令牌跳跃和令牌滑动。在问题的令牌跳跃变体中，一个步骤允许令牌从一个顶点跳到图中的任何其他顶点。在令牌滑动变体中，令牌只能从顶点滑到其一个邻居之一。像独立集问题一样，上述两个问题均为w [1] - hard在一般图上（对于参数k）。非常富有成果的研究线[5，14，27，25]表明，当仅限于稀疏的图形类别（例如平面，有界的树宽，无处浓度，并且一直到无biclique for biclique for biclique for biclique for biclique for biclique for biclique tograph，opertion set问题都可成为固定参数。在一系列论文中，也证明了这一论文可以解决令牌跳跃问题[17、22、26、8]。至于令牌滑动问题（在大多数这些论文中都提到，除了该问题是在树上可以解决的多项式时间[11]和间隔图[6]之外，几乎没有什么知道的。我们通过引入一个新的模型来重新配置独立集，我们称之为银河系重新配置。使用此新模型，我们表明（标准）令牌滑动是固定参数可以在有界集团数字的有界度，平面图和弦图的图表上进行操作。我们认为，银河重新配置模型具有独立的兴趣，并且有可能有助于解决有关令牌滑动的（参数化）复杂性的剩余开放问题。
更快的3彩色图形 - 滴
n log n）。在多项式时间内是否可以解决该问题仍然是算法图理论领域的一个众所周知的开放问题。在本文中，我们提出了一种算法，该算法在时间2 o（n 1/3 log 2 n）中求解n-vertex直径-2图中的3-着色。这是对Mertzios和Spirakis算法的第一个改进，即在一般情况下，即没有对实例图进行任何进一步的限制。除了标准分支并将问题减少到2-SAT的实例外，我们算法的关键构建块是关于3色直径-2图的组合观察，使用概率参数证明了这一点。作为侧面结果，我们表明可以在时间2 o（（n log n）2 /3）中求解3-颜色。我们还将算法推广到从小直径图到周期中找到同态同态的问题。
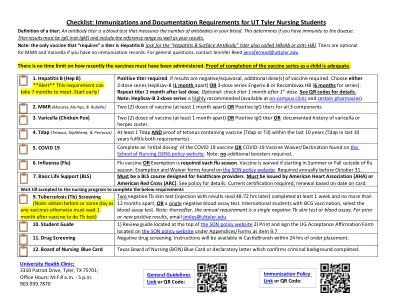
免疫接种和文件要求清单。......
需要阳性滴度。如果结果为阴性/可疑，则需要额外剂量的疫苗。选择 2 剂系列 Heplisav-B（间隔 1 个月）或 3 剂系列 Engerix-B 或 Recombivax HB（系列间隔 6 个月）。在最后一次剂量后 1 个月重复滴度。可选：在第一次剂量后 1 个月检查滴度。详情请参阅二维码。注意：强烈推荐 Heplisav-B 2 剂系列（可在校内诊所和某些药房购买）2. MMR（麻疹、腮腺炎和风疹）两 (2) 剂疫苗（至少间隔 1 个月）或所有 3 种成分的 IgG 滴度均为阳性