XiaoMi-AI文件搜索系统
World File Search System人工智能与机器学习
项目名称 理学学士 – 人工智能与机器学习 课程代码/名称 UGAM101 / 线性代数与微积分 年份/学期 I / ILTPC 3 1 0 4 课程目标: 1. 用矩阵方法解释线性方程组的解。 2. 讨论级数的收敛和发散。 3. 解释二元函数的偏导数和极值 4. 讨论标量和矢量函数的物理解释 5. 讨论矢量线、曲面和体积积分。 课程成果: 成功完成课程后,学生将能够: 1. 应用矩阵方法解线性方程组 2. 测试无限级数的收敛和发散。 3. 确定二元函数的极值。 4. 将向量微分算子应用于标量和向量函数 5. 用格林函数求解线、表面和体积积分,UNIT-I 矩阵 12 矩阵的秩、梯形、线性方程组的一致性、向量的线性依赖性、特征值、特征向量、特征值的性质、凯莱-哈密顿定理、二次型、通过线性变换将二次型简化为标准形式、二次型的性质。UNIT-II 无穷级数 12 数列和级数收敛的定义。正项级数 – 收敛的必要条件、比较检验、极限形式比较检验、达朗贝尔比率检验、拉贝检验、柯西根检验、交错级数、莱布尼茨规则、绝对和条件收敛。 UNIT-III 偏微分及其应用 12 两个或多个变量的函数,偏导数,高阶偏导数,全导数,隐函数的微分,雅可比矩阵,两个变量函数的泰勒展开式,两个变量函数的最大值和最小值。 UNIT-IV 向量微分学 12 标量和向量点函数,向量算子 Del,梯度,方向导数,散度,旋度,Del 两次应用于点函数,Del 应用于点乘积
使用简化公式计算量子计算的散射振幅
利用 Lehmann-Symanzik-Zimmermann 约化公式,我们提出了一种新的通用框架,用于以完全非微扰的方式使用量子计算机计算量子场论中的散射振幅。在这个框架中,只需要构建零动量的单粒子状态,不需要入射粒子的波包。该框架能够结合束缚态的散射,非常适合涉及少量粒子的散射。我们预计该框架在应用于独有的强子散射时会具有特殊优势。作为概念证明,通过在经典硬件上进行模拟,我们证明了在单味 Gross-Neveu 模型中,从我们提出的量子算法中获得的费米子传播子、连通费米子四点函数和费米子-反费米子束缚态的传播子具有实现 Lehmann-Symanzik-Zimmermann 约化公式所必需的所需极点结构。
第一年工学学士学位课程的共同课程...
模块3[8L] 数列和级数:数列和级数收敛的基本概念;收敛检验:比较检验、柯西根检验、达朗贝尔比检验(这些检验的语句和相关问题)、拉贝检验;交错级数;莱布尼茨检验(仅语句);绝对收敛和条件收敛。 模块4[10L] 多元函数微积分:多元函数简介;极限和连续性、偏导数、三元以下齐次函数和欧拉定理、链式法则、隐函数的微分、全微分及其应用、三元以下雅可比矩阵最大值、最小值;函数的鞍点;拉格朗日乘数法及其应用;线积分的概念,二重和三重积分。模块 5[10L] 向量微积分:标量变量的向量函数,向量函数的微分,标量和向量点函数,标量点函数的梯度,向量点函数的散度和旋度,
第一年的普通课程B. Tech ...
模块-3 [8L]序列和序列:序列和序列收敛的基本概念;收敛的测试:比较测试,Cauchy的根测试,D'Alembert的比率测试(这些测试中的语句和相关问题),Rabbe的测试;交替系列;莱布尼兹的测试(仅说明);绝对收敛和条件收敛。模块-4 [10L]几个变量功能的计算:几个变量的功能简介;极限和连续性,部分衍生物,均质函数和Euler定理最多三个变量,链条规则,隐式函数的差异,总差分及其应用,雅各布人最多三个变量最大值,minima;鞍座的鞍点; Lagrange乘数方法及其应用程序;线积分,双重和三个积分的概念。模块-5 [10L]矢量计算:标量变量的向量函数,向量函数的差异,标量和向量点函数,标量点函数的梯度,矢量函数的差异和curl,
量子宇宙的信号
人们普遍认为宇宙的结构起源于加速膨胀早期的量子涨落。然而,我们今天观察到的模式并不能区分量子涨落和经典的原始涨落;目前的宇宙学数据与这两种可能性都一致。我们在此认为,检测原始非高斯性可以解决目前的情况,并为宇宙结构的量子起源提供试金石。与量子力学不同,真空涨落不能出现在经典理论中,因此长距离经典关联必须来自初始状态的(真实)粒子。与平坦空间散射过程类似,我们展示了基本原理如何要求这些粒子在所谓的折叠配置中表现为 n 点函数中的极点。根据这一观察,并假设涨落 (i) 在大尺度上相关,(ii) 由膨胀阶段的局部演化产生,我们证明非高斯相关器的折叠极限中没有极点唯一地标识了量子真空是初始状态。本着与贝尔不等式相同的精神,我们讨论了如果放弃局部性,如何能避免这种情况。
神经网络的非微扰重正化-...
在最近的一项工作 [ 1 ] 中,Halverson、Maiti 和 Stoner 提出了一种用威尔逊有效场论来描述神经网络的方法。无限宽度极限被映射到自由场论,而有限 N 个校正则由相互作用(作用中的非高斯项)考虑。在本文中,我们研究了这种对应的两个相关方面。首先,我们在这种情况下评论了局部性和幂计数的概念。事实上,这些通常的时空概念可能不适用于神经网络(因为输入可以是任意的),然而,重正化群提供了局部性和缩放的自然概念。此外,我们还评论了几个微妙之处,例如数据分量可能不具有置换对称性:在这种情况下,我们认为随机张量场论可以提供自然的概括。其次,我们通过使用 Wetterich-Morris 方程提供非微扰重正化群的分析,改进了 [1] 中的微扰威尔逊重正化。与通常的非微扰 RG 分析的一个重要区别是,只知道有效 (IR) 2 点函数,这需要谨慎设定问题。我们的目标是提供一种有用的形式化方法,以非微扰方式研究超越大宽度极限(即远离高斯极限)的神经网络行为。我们分析的一个主要结果是,改变神经网络权重分布的标准差可以解释为网络空间中的重正化流。我们专注于平移不变核并提供初步的数值结果。
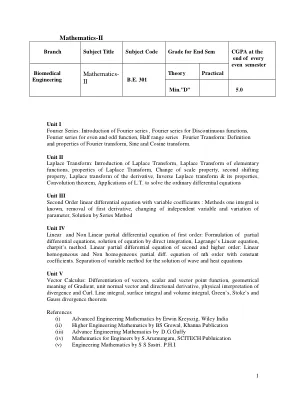
数学-II - 分支学科名称学科代码年级...
第一单元 傅里叶级数:傅里叶级数简介、不连续函数的傅里叶级数、偶函数和奇函数的傅里叶级数、半程级数 傅里叶变换:傅里叶变换的定义和性质、正弦和余弦变换。 第二单元 拉普拉斯变换:拉普拉斯变换简介、初等函数的拉普拉斯变换、拉普拉斯变换的性质、尺度变化性质、二阶平移性质、导数的拉普拉斯变换、逆拉普拉斯变换及其性质、卷积定理、应用 LT 解常微分方程 第三单元 变系数二阶线性微分方程:方法 已知一个积分、去除一阶导数、改变独立变量和改变参数、用级数法求解 第四单元 一阶线性和非线性偏微分方程:偏微分方程的公式、直接积分解方程、拉格朗日线性方程、查皮特方法。 二阶及高阶线性偏微分方程:具有常系数的 n 阶线性齐次和非齐次偏微分方程。分离变量法解波动和热方程 第五单元 向量微积分:向量的微分、标量和向量点函数、梯度的几何意义、单位法向量和方向导数、散度和旋度的物理解释。线积分、面积积分和体积积分、格林散度定理、斯托克斯散度定理和高斯散度定理 参考文献
安全无忧的软件租赁
众所周知,量子密码学可以实现仅使用经典信息无法实现的功能。最近,安全软件租赁 (SSL) 已成为这些感兴趣的领域之一。给定一个来自电路类的目标电路 C,SSL 会生成 C 的编码,使接收者能够评估 C ,还使软件的创建者能够验证软件是否已返回 — 这意味着接收者已放弃进一步使用该软件的可能性。显然,仅使用经典信息无法实现这样的功能,因为不可能阻止用户保留软件的副本。最近的结果表明,对于一类称为计算和比较的函数(这些是众所周知的点函数的概括),使用量子信息可以实现 SSL。然而,这些先前的工作都利用了设置或计算假设。在这里,我们表明 SSL 可以在没有任何假设的情况下用于计算和比较电路。我们的技术涉及量子复制保护的研究,这是一个与 SSL 相关的概念,但编码过程本质上可以防止潜在的量子软件盗版者将 C 的编码的单个副本拆分为两部分,每个部分都允许用户评估 C 。我们表明,对于涉及一个诚实评估者和一个恶意评估者的新型安全定义,点函数可以在没有任何假设的情况下进行复制保护;这是通过证明从任何量子消息认证代码中,我们都可以推导出这样一个诚实-恶意复制保护方案来实现的。然后,我们表明,通用的诚实-恶意复制保护方案意味着 SSL;根据先前的工作,这为计算和比较函数提供了 SSL。
超音速飞行中复合板的气动弹性不稳定性...
研究超声速气流作用下复合材料层合板的气动弹性失稳问题,通过求解气动弹性特性的广义特征值问题进行分析。通常通过计算不同来流速度下层合结构的固有频率,得到层合板在气流作用下的临界失稳速度,这是由于层合结构刚度减小,导致结构失稳。应根据复合材料壁板所处的力学环境合理设计结构参数,避免在气流作用下出现结构失稳问题。活塞理论最初由Lighthill在Hayes对Tsien高超声速相似理论的扩展基础上发展起来。在壁板颤振研究中,为了更好地模拟实际的气动变化过程,许多研究者提出了各种气动计算模型,但这些气动模型的不足之处在于考虑了较为复杂的边界条件,因此方程的求解过程相当复杂。在结构力学的框架下,利用二维模型,利用活塞理论推导了能够预报超声速范围内先进结构壁板颤振的精细气动弹性模型。活塞理论被广泛应用于许多气动模型,它提供了体表某点处表面下洗流与气动压力之间的准定常点函数关系。这使得活塞理论成为一种计算成本低廉的空气动力学模型。在本论文中,CUF工具的高效性允许推导任意阶模型,Carrera统一公式允许使用紧凑统一的公式推导任何模型。强形式解和提出的CUF模型的有限元近似。本文推导了二维模型的FEM特征矩阵,基本核允许使用自动程序推导矩阵。有限元法(FEM)由于其多功能性和数值效率而仍然值得关注。已经解决了力学的各种问题,包括静态,自由振动和动态响应问题。通过求解气动弹性特性的广义特征值问题对其进行分析,并考虑了许多参数来研究它们对颤振边界的影响。关键词:有限元方法、活塞理论、气动弹性不稳定性、气动弹性、Carrera 统一公式、超音速、复合层压板。