XiaoMi-AI文件搜索系统
World File Search System开发细长的椭圆形热源模型,以减少定向能量沉积过程的计算时间
金属零件的定向能量沉积(DED)添加剂制造过程越来越流行,并且由于它们制造大尺寸的一部分的潜力而被广泛接受。由于过程物理学而获得的复杂热循环导致残留应力和失真的积累。但是,为了准确地对大零件的金属沉积传热进行建模,数值模型会导致不切实际的计算时间。在这项工作中,开发了具有安静/主动元件激活的3D瞬时元素模型,用于建模金属沉积传热过程。为了准确地模拟移动热源,戈德克的双椭圆形模型的实现是用足够小的模拟时间增量来实现的,从而使激光在每个增量过程中移动其半径的距离。考虑使用不同工艺参数制造的不锈钢316L的薄壁壁,用COMSOL 5.6多物理软件获得的数值结果通过在制造20层的底物上记录的实验温度数据成功验证。为了减少计算时间,实现了整个路径上的热源的拉长椭圆形热输入模型。已经发现,通过采取如此大的时间增量,数值模型会产生不准确的结果。因此,该轨道分为几个子轨道,每个子轨道都以一个模拟增量应用。另外,引入了校正因子,该校正因子进一步减少了伸长热源的计算误差。在这项工作中,进行了调查,以发现正确的模拟时间增量或子轨道大小,从而导致计算时间减少(5 - 10次),但仍会产生非常准确的结果(低于温度相对误差的10%)。最后,在发现正确的时间增量大小和校正因子值以减少计算时间产生准确结果的情况下,还建立了新的相关性。
对导航级 RLG SIMU 类型 iNAV-RQH 的调查
本研究介绍了使用我们的环形激光陀螺仪 ( RLG ) 导航级捷联惯性测量单元 ( SIMU ) 类型 iNAV-RQH 进行的特性和一些评估实验结果,精度为 1 nmi/h。在简要介绍 SIMU 的主要特征后,给出了惯性传感器构造原理和误差模型的描述。为了评估我们的捷联 IMU,我们设计了实验室和现场测试,在中等精度转盘和汽车导航任务框架内进行,使用 DGPS(差分 GPS)参考解决方案(在我们的案例中,是一种即时 ( OTF ) 运动学 DGPS 解决方案,在整数秒的常规时期提供精确的位置参考)。使用专用软件 Kingspad 获得后处理的 3-D 惯性或集成 GPS/INS 解决方案。还介绍了噪声和误差分析,以及实验室和现场测试的具体结果。位置精度在亚 dm 域内(与 cm 精度 DGPS 参考轨迹的差异,1-σ 相对误差约为 1 cm),驱动轨迹周长分别为数百米。加速度误差在 mGal 域内(经过约 60…100 秒的适当过滤后),姿态误差在角秒范围内,iMAR 的 RLG SIMU 类型 iNAV-RQH 被认为完全适合精确导航、测量和精确重力测定。[Dorobantu et al., 2004] 中已经给出了一些初步结果,目前的扩展形式包括传感器技术和误差模型的更多内部内容,以及使用 ZUPT s(惯性导航系统零速度更新)的室内 INS 导航实验。附录中介绍了补充实验,如静态倾斜、阻尼测试或 SIMU 的静态评估,以及对 ISA(惯性传感器组件)的更多了解,或从已注册的 SIMU 数据直接推导大地测量参数。
估计标准偏差占其真实值的百分比所需的样本量
当需要估计标准差时,经常需要合理选择样本量。在许多情况下,将估计的允许误差从绝对误差改为相对误差是可以接受的,并且可以对样本量问题进行精确的先验解,而无需涉及任何先前的估计。在许多实际工程情况下,需要估计特征的线性离散度。这样的例子有低空炸弹瞄准器的纵向或范围误差,或测量设备的误差。与工程师合作的经验表明:1)他掌握了标准差作为离散度度量的概念;2)他接受将样本标准差表示为在先前商定的正常总体真实值的百分比范围内的概念; 3) 他对置信系数有足够的直观理解,愿意采取相应的行动。因此,有一种快速的方法可以告诉他获取不同置信系数的各种置信区间内的估计值所需的样本量。这些估计值是将真实标准差的置信区间的半长表示为真实标准差的百分比。为估计这一点所需的样本量而提出的解决方案不使用任何先前的离散估计或其真实值,因此适用范围很广。假设正在对正态总体进行抽样。让 82 成为总体 o2 的平方标准差的估计值,使得 ns2/o-2 分布为具有 n 个自由度的 X2。那么 s2 的平均值将为 E(s2) = u2,其中 u2 是真实但未知的总体方差。设 0 如果我们知道概率{s>(1+u)u} =pi,以及概率{s<(1-u)u} =P2,那么 s 位于 u 的给定分数 u 内的时间比例将是已知的。 pi 和 P2 的值是通过以下关系获得的。如果我们知道概率{s>(1+u)u} =pi,以及概率{s<(1-u)u} =P2,那么 s 位于 u 的给定分数 u 内的时间比例将是已知的。pi 和 P2 的值是通过以下关系获得的。
基于人口发射速率的电动脑信号预测的有效性
通过测量局部田间电位(LFP)或脑电图(EEG)信号(EEG)信号(EEG)信号(EEG)信号(EEG)信号,通常对人群水平的神经活动进行实验研究。为了进行观察到的神经活动和模拟神经活动之间的比较,重要的是,神经活动的模拟可以准确预测这些大脑信号。在人群层面上对神经敏化的模拟通常依赖于点神经元网络模型或点火率模型。虽然这些简化的神经活动的表示在计算上是有效的,但它们缺乏计算LFP/EEG信号所需的明确空间信息。已经提出了不同的启发式方法来克服这一限制,但是这些方法的准确性尚未得到充分评估。这样一种启发式方法,即所谓的内核方法,以前已采用有希望的结果,并且具有在电动脑信号产生的生物物理学中得到充分依据的其他优势。它基于网络模型中每个突触途径的计算速率至lfp/eeg kernels,之后可以直接从人口发射速率获得LFP/EEG信号。这相当于计算大脑信号的计算工作量的大规模降低,因为为每个人群计算大脑信号,而不是为每个神经元计算。在这里,我们研究了如何以及何时可以期望内核方法起作用,并提出了预测其准确性的理论框架。最后,我们证明了内核方法对于主导大脑信号的贡献最准确。我们表明,脑信号预测的相对误差是单细胞内核异质性和尖峰训练相关性的函数。因此,我们进一步建立了内核法作为一种有希望的方法,用于计算大型神经模拟的电信号。
深度学习的投影空间实施 -
我们的目的是评估低剂量(LD)PET图像和辛图中的全剂量(FD)PET图像合成的性能,而无需使用深度学习技术牺牲诊断质量。方法:回顾性使用140例患者的临床脑PET/CT研究。从FD列表模式PET数据中随机选择了5%的事件,以模拟现实的LD采集。促进了一个修改的3维U-NET模型,以分别从相应的LD辛图和图像中预测图像空间(PIS)中的投影空间(PSS)和FD图像中的FD曲目。使用5分评分方案评估了2个核医学专家的预测PET图像的质量。使用已建立的指标进行定量分析,包括峰值信噪比(PSNR),结构相似性指数指标(SSIM),区域性SUV偏置以及83个大脑区域中的第一,第二和高阶纹理放射线特征,用于测试和评估数据集中的83个大脑区域。结果:所有PSS图像均由核医学专家评分4或更高(良好至优秀)。PSNR和SSIM值分别为0.96±0.03和0.97±0.02,PSS分别获得了31.70±0.75和37.30±0.71的值。在所有大脑区域中计算出的平均SUV偏置分别为PSS和PI分别为0.24%±0.96%和1.05%±1.44%。与参考FD图像相比,PSS的平淡 - Altman图报告了PSS的最低SUV BI- AS(0.02)和方差(95%的置次间隔,-0.92至1 0.84)。PIS和PSS分别属于灰级共振矩阵类别的同质性放射线特征的相对误差分别为-1.07±1.77和0.28±1.4。结论:定性评估和定量分析表明,FD PET PSS提高了性能,从而提高了图像质量,而SUV偏置和方差较低,而SUV PET和差异要比FD PET PIS。
高斯过程回归杂交模型,用于顶级...
摘要:越来越多的光学卫星任务对陆地地球系统的连续监测为植被和农田特征提供了宝贵的见解。卫星任务通常提供不同级别的数据,例如1级大气顶(TOA)辐射率和2级大气底(BOA)反射率产品。开发TOA辐射数据直接提供了绕过复杂大气校正步骤的优势,在该步骤中,错误可以在其中进行预测并损害随后的检索过程。因此,我们研究的目的是开发能够从成像光谱卫星任务中直接从TOA辐射数据中检索植被特征的模型。为了实现这一目标,我们基于辐射转移模型(RTM)模拟数据构建了混合模型,从而采用了植被范围RTM与大气libradtran RTM结合使用高斯工艺回归(GPR)。重点是植被冠层特征的重新评估,包括叶子面积指数(LAI),冠层叶绿素含量(CCC),冠层水含量(CWC),吸收的光合式活性辐射(FAPAR)的分数以及植被覆盖的分数(FVC)。使用即将到来的哥白尼高光成像任务(Chime)的带设置,评估了两种类型的混合GPR模型:(1)使用TOA辐射数据在1级(L1)培训的一种培训,并且(2)使用BOA反射率数据在2级(L2)训练。基于TOA和BOA的GPR模型均已针对原位数据验证,并具有从现场活动中获得的相应高光谱数据。基于TOA的混合GPR模型揭示了从中度到最佳结果的一系列性能,因此达到R 2 = 0.92(LAI),R 2 = 0.72(CCC)和0.68(CCC)和0.68(CWC),R 2 = 0.94(FAPAR)和R 2 = 0.95(FVC)。为了证明模型的适用性,随后将基于TOA和BOA的GPR模型应用于科学前体任务Prisma和Enmap的图像。所产生的性状图在基于TOA和BOA的模型之间显示出足够的一致性,相对误差在4%至16%之间(R 2在0.68和0.97之间)。总的来说,这些发现阐明了机器学习混合模型的开发和增强的路径,以估算直接在TOA水平下定制的植被特征。
使用模糊推理的几何特征和过程参数优化激光沉积AISI 316钢
1生产工程毕业后计划,巴西圣保罗卫理公会大学。2工程学校,麦肯齐长老会大学,圣保罗,巴西。3古巴圣地亚哥de Cuba的Oriente University机械与工业工程学院。 4巴拉那帕拉纳帕拉纳联邦技术大学的客座教授。 5 Insper-巴西圣保罗教育与研究所。 *通讯作者:dtasev88@gmail.com摘要激光金属沉积(LMD)工艺是一种增材制造技术,由于其能力具有复杂的几何形状和不同类型的金属材料,因此吸引了汽车和航空工业的兴趣。 但是,沉积层的结构和制成部分的几何特性受沉积过程参数之间的相互作用的影响。 在本文中,使用模糊推理(FIS)技术来开发两个模型,以预测几何特性,并使用AISI 316不锈钢粉末和底物优化LMD工艺参数。 基于阶乘分析的实验设计用于将所选沉积过程参数,激光功率(LP),粉末流量(PF)和焦距(FL)与过程的几何特征珠高(BH),珠宽度(BW),渗透深度(DP),渗透(DP)和湿度(DP)和湿度(WA)相关联。 因子LP和FL使用三个操作水平:LP = 225 W,250 W,275 W,FL = 4.8 mm,5.0 mm,5.2 mm。 使用两个级别的因子PF,9.40 g/s和13.35 g/s。3古巴圣地亚哥de Cuba的Oriente University机械与工业工程学院。4巴拉那帕拉纳帕拉纳联邦技术大学的客座教授。5 Insper-巴西圣保罗教育与研究所。 *通讯作者:dtasev88@gmail.com摘要激光金属沉积(LMD)工艺是一种增材制造技术,由于其能力具有复杂的几何形状和不同类型的金属材料,因此吸引了汽车和航空工业的兴趣。 但是,沉积层的结构和制成部分的几何特性受沉积过程参数之间的相互作用的影响。 在本文中,使用模糊推理(FIS)技术来开发两个模型,以预测几何特性,并使用AISI 316不锈钢粉末和底物优化LMD工艺参数。 基于阶乘分析的实验设计用于将所选沉积过程参数,激光功率(LP),粉末流量(PF)和焦距(FL)与过程的几何特征珠高(BH),珠宽度(BW),渗透深度(DP),渗透(DP)和湿度(DP)和湿度(WA)相关联。 因子LP和FL使用三个操作水平:LP = 225 W,250 W,275 W,FL = 4.8 mm,5.0 mm,5.2 mm。 使用两个级别的因子PF,9.40 g/s和13.35 g/s。5 Insper-巴西圣保罗教育与研究所。*通讯作者:dtasev88@gmail.com摘要激光金属沉积(LMD)工艺是一种增材制造技术,由于其能力具有复杂的几何形状和不同类型的金属材料,因此吸引了汽车和航空工业的兴趣。但是,沉积层的结构和制成部分的几何特性受沉积过程参数之间的相互作用的影响。在本文中,使用模糊推理(FIS)技术来开发两个模型,以预测几何特性,并使用AISI 316不锈钢粉末和底物优化LMD工艺参数。基于阶乘分析的实验设计用于将所选沉积过程参数,激光功率(LP),粉末流量(PF)和焦距(FL)与过程的几何特征珠高(BH),珠宽度(BW),渗透深度(DP),渗透(DP)和湿度(DP)和湿度(WA)相关联。因子LP和FL使用三个操作水平:LP = 225 W,250 W,275 W,FL = 4.8 mm,5.0 mm,5.2 mm。使用两个级别的因子PF,9.40 g/s和13.35 g/s。差异分析允许识别PF影响BH,BH/BW比率,D和WA。激光功率(LP)的增加导致几何特征BW和DP的增加。第一个FI,用于预测珠的几何特性,具有高足够的(相对误差高达8.43%),用于评估EX的体验条件。考虑到所研究的工作条件和评估的变量,第二FI表示最佳相互作用。使用沉积过程参数LP = 250 W,FL = 5 mm,PF = 9.40 g/s,获得了最大输出解体指数(ODI = 0.845)。关键字:激光金属沉积,模糊推理,珠几何预测,沉积过程参数,AISI 316不锈钢1.简介
定量2D和3D相对比MRI
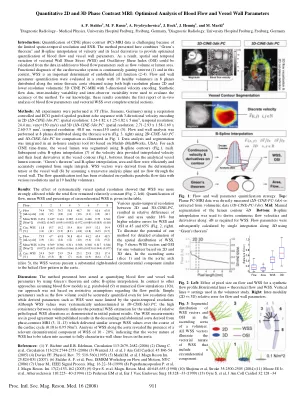
定量2D和3D期对比MRI:血流和血管壁参数的优化分析A.德国弗雷堡(Freiburg)简介:由于时空分辨率和SNR的有限,CINE相对比(PC)-MRI数据的量化很具有挑战性。此处介绍的方法结合了速度及其局部衍生物的“格林定理”和B型插值插值,以提供优化的血流和容器壁参数的定量。结果,除血流量参数(如流量量或流体面积)外,还可以从数据中计算出矢量壁剪应力(WSS)和振荡剪切指数(OSI)的空间和时间变化。心血管系统的功能诊断是不断获得兴趣的(1),在这种情况下,WSS是内皮细胞功能的重要决定因素(2-4)。流量和壁参数定量,其中有19个健康志愿者在8个平面中,沿着整个胸主动脉分布,使用高分辨率平面2D和较低分辨率的体积3D Cine PC-MRI,并具有3个方向速度编码。合成流数据,模式间可变性和观察者间的可变性用于评估该方法的准确性。据我们所知,这些结果构成了对完整动脉切片的血流参数和矢量WSS的体内分析的首次报告。1。2,左)。2,右)。Methods: All experiments were performed at 3T (Trio, Siemens, Germany) using a respiration controlled and ECG gated rf-spoiled gradient echo sequence with 3-directional velocity encoding in 2D ( 2D-CINE-3dir.PC : spatial resolution: 1.24-1.82 x 1.25-1.82 x 5 mm 3 , temporal resolution: 24.4 ms, Venc = 150 cm/s)和3D(3D-Cine-3ddir.pc:空间分辨率:2.71-2.93 x 1.58-1.69 x 2.60-3.5 mm 3,时间分辨率:48.8 ms,48.8 ms,Venc = 150 cm/s)(5)(5)。在沿胸主动脉分布的8个平面上进行进行壁分析(图 3,右)使用2d-cine-3ddir.pc和3d-cine-3ddir.pc进行比较,如图所示 数据分析和细分集成在基于MATLAB(美国Mathworks)的内部分析工具(6)中。 对于每个Cine时间框架,使用B-Spline轮廓分割了血管腔(图1,MID)。 随后的速度数据的立方B型插值(7)提供了插值速度及其在容器轮廓处的局部衍生物(图1,底部)。 基于分析血管腔轮廓,“ Green's Theorem”和B-Spline插值,面积和流量是从单个积分中有效且准确地计算出来的。 WSS载体是通过假设横向分析平面而没有流过容器壁的变形张量(8)的变形张量。 流量定量工具已通过各种分辨率和19位健康志愿者的合成抛物线流数据进行评估。 结果:系统多样化的空间分辨率的影响表明,WSS受到更大的影响,而总流量保持相对恒定(图 参考:(1)Y. Richter和E.R.进行壁分析(图3,右)使用2d-cine-3ddir.pc和3d-cine-3ddir.pc进行比较,如图数据分析和细分集成在基于MATLAB(美国Mathworks)的内部分析工具(6)中。对于每个Cine时间框架,使用B-Spline轮廓分割了血管腔(图1,MID)。随后的速度数据的立方B型插值(7)提供了插值速度及其在容器轮廓处的局部衍生物(图1,底部)。基于分析血管腔轮廓,“ Green's Theorem”和B-Spline插值,面积和流量是从单个积分中有效且准确地计算出来的。WSS载体是通过假设横向分析平面而没有流过容器壁的变形张量(8)的变形张量。流量定量工具已通过各种分辨率和19位健康志愿者的合成抛物线流数据进行评估。结果:系统多样化的空间分辨率的影响表明,WSS受到更大的影响,而总流量保持相对恒定(图参考:(1)Y. Richter和E.R.表中给出了流量,平均WSS和圆周WSS的百分比。2D和3D-Cine-PC之间的各种时空分辨率导致流量和面积的相对差异在18%以下,但WSS和OSI的相对误差较高,而OSI则为45%和65%(图。说明了我们方法对WSS空间分布进行详细评估的潜力,图3显示了基于2D和3D数据的一名志愿者的WSS向量和OSI。在上升主动脉(切片1)和主动脉弓(切片3)中,WSS矢量呈现出与主动脉中螺旋流量模式相似的实质性右手圆周分量。讨论:此处介绍的方法旨在使用Green的定理和Cubic B-Spline插值来量化血流和血管壁参数。与假设血流模型的其他方法相反(例如抛物面(9)或数值流仿真(10)),我们的方法不是基于关于流量轮廓的限制性假设。简单的参数,例如流量量,即使对于低分辨率数据也可以准确量化,而诸如WSS之类的派生参数则受到时空分辨率的限制。尽管WSS值在3D-Cine-3dir.pc中被系统地低估了,但志愿者之间的高一致性表明了对相对病理WSS改变的分析的潜在WSS估计,如最初的患者结果所示。Edelman,《流通》 113:2679-2682(2006)(2)Cheng C.等,循环113(23):2744-2753(2006)(2006)(3)Wentzel J.J.等,J Am Coll Cardiol。 45:846-54(2005)(4)Davies PF,Physiol。 修订版Edelman,《流通》 113:2679-2682(2006)(2)Cheng C.等,循环113(23):2744-2753(2006)(2006)(3)Wentzel J.J.等,J Am Coll Cardiol。45:846-54(2005)(4)Davies PF,Physiol。修订版我们的WSS测量值与源自相比的MRI的下降和腹主动脉(3,11-13)的发表结果非常吻合,该结果在心脏周期中提供了相似的平均WSS值(0.18至0.95至0.95 N/M 2)。对WSS沿主动脉的分析表明,WSS的相关圆周成分的存在为10-20%,这表明必须考虑WSS的向量性质以完全表征主动脉中的壁剪力。75:519-560(1995)(5)Markl M.等,J Magn Reson IM。 25:824-831(2007)。 (6)Stalder A. F.等,Proc。 ISMRM流动和运动研讨会,纽约(2006)(7)Unser M.,IEEE信号过程。 mag。 16 22–38(1999)(8)Papathanasopoulou P.等,J。Magn。 共振。 im。 17(2):153-162(2003)(9)Oyre S.等,Magn。 共振。 Med。 40:645-655(1998)(10)Shojima等,中风35:2500-2505(2004)(11)Moore Je Jr.等,动脉粥样硬化110:225-40(1994)(1994)(1994)(12) 32:128 –3475:519-560(1995)(5)Markl M.等,J Magn Reson IM。25:824-831(2007)。 (6)Stalder A. F.等,Proc。 ISMRM流动和运动研讨会,纽约(2006)(7)Unser M.,IEEE信号过程。 mag。 16 22–38(1999)(8)Papathanasopoulou P.等,J。Magn。 共振。 im。 17(2):153-162(2003)(9)Oyre S.等,Magn。 共振。 Med。 40:645-655(1998)(10)Shojima等,中风35:2500-2505(2004)(11)Moore Je Jr.等,动脉粥样硬化110:225-40(1994)(1994)(1994)(12) 32:128 –3425:824-831(2007)。(6)Stalder A. F.等,Proc。ISMRM流动和运动研讨会,纽约(2006)(7)Unser M.,IEEE信号过程。mag。16 22–38(1999)(8)Papathanasopoulou P.等,J。Magn。共振。im。17(2):153-162(2003)(9)Oyre S.等,Magn。共振。Med。40:645-655(1998)(10)Shojima等,中风35:2500-2505(2004)(11)Moore Je Jr.等,动脉粥样硬化110:225-40(1994)(1994)(1994)(12) 32:128 –34