XiaoMi-AI文件搜索系统
World File Search System真空环境下的线性编码器
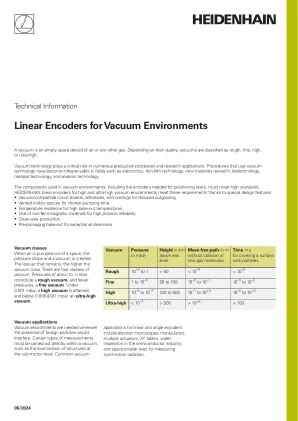
低释气性为防止真空室内压力急剧升高,真空兼容编码器不得释放大量气体。在超高真空中,每个部件都至关重要。例如,某些塑料会释出溶剂。这类塑料通常包含在电路板、粘合剂或涂层中,但在超高真空环境中部署的设备中应完全避免使用。这就是海德汉公司采用真空兼容电路板、粘合剂和涂层的原因。在超高真空环境中,必须将部件数量减至最少。例如,信号转换器应放在真空室外,这就是海德汉公司提供带有外部信号转换器的真空兼容编码器的原因。在仅需要高真空的应用中,这些设备也可放置在真空室内。
轴P7316视频编码器
轴P7316是一个功能齐全的16通道视频编码器,可为任何模拟摄像机系统增加IP好处。它支持标准和高清模拟摄像机,最大分辨率为4K,以及RS485的PTZ控制。此机架安装的编码器具有双向音频和智能分析的支持,例如运动检测和主动篡改警报。SFP插槽可实现长距离光纤连接和网络冗余。轴P7316包括邮政流,并支持H.264/H.265,以大大降低带宽和存储要求。此外,它提供内置的网络安全功能,例如签名固件和安全启动。
利用变分自动编码器进行生成主动学习,用于兽医学放射学数据生成
摘要 — 近年来,随着人们对宠物保健的兴趣日益浓厚,兽医对计算机辅助诊断 (CAD) 系统的需求也随之增加。由于缺乏足够的放射学数据,兽医 CAD 的发展陷入停滞。为了克服这一挑战,我们提出了一种基于变分自动编码器的生成主动学习框架。此方法旨在缓解兽医 CAD 系统可靠数据的稀缺问题。本研究利用了包括心脏扩大放射图像数据和慢性肾病超声图像数据的数据集。在删除注释并标准化图像后,我们采用了一个数据增强框架,该框架包括数据生成阶段和用于过滤生成数据的查询阶段。实验结果表明,当通过该框架生成的数据添加到生成模型的训练数据中时,射线图像中的 frechet 起始距离从 84.14 减小到 50.75,超声图像中的 frechet 起始距离从 127.98 减小到 35.16。随后,当生成的数据被纳入分类模型的训练中时,混淆矩阵的真负数也从射线照片上的 0.16 提高到 0.66,超声图像上的真负数从 0.44 提高到 0.64。所提出的框架有可能解决医学 CAD 数据稀缺的挑战,从而促进其发展。
感知少,生成更多:用蒙版自动编码器进行超高效率3D传感的训练激光雷达感知
摘要 - 在这项工作中,我们提出了一种破坏性节俭的激光雷达感知数据流,该数据流产生而不是感知环境的一部分,这些部分是基于对环境的广泛培训,或者对整体预测准确性的影响有限的。因此,所提出的方法将传感能量与训练数据进行交易,以获取低功率机器人和自动导航,以便用传感器省将,从而在一次电池充电时延长了其寿命。我们提出的为此目的提出的生成预训练策略称为径向掩盖的自动编码(R-MAE),也可以在典型的激光雷达系统中很容易实施,通过选择性激活和控制在现场操作过程中随机生成的角区域的激光功率。我们的广泛评估表明,使用R-MAE进行预训练可以重点关注数据的径向段,从而比常规程序更有效地限制了空间关系和对象之间的距离。因此,所提出的方法不仅降低了传感能量,而且还提高了预测准确性。例如,我们对Waymo,Nuscenes和Kitti数据集进行了广泛的评估表明,该方法在跨数据集的检测任务的平均精度提高了5%,并且从Waymo和Nuscenes转移到Kitti的检测任务的平均精度提高了4%。在3D对象检测中,它在KITTI数据集中的中等难度水平下,在AP中最多可增强小对象检测。即使使用90%的径向掩蔽,它在Waymo数据集中所有对象类中的MAP/MAPH中都超过了基线模型。此外,我们的方法在Nuscenes数据集上分别获得了MAP和NDS的3.17%和2.31%的提高,这表明了其在单个和融合的LIDAR相机模态方面的有效性。代码可在https://github.com/sinatayebati/radial Mae上公开获取。索引项 - lidar预训练,掩盖自动编码器,超有效的3D传感,边缘自治。
使用变分自编码器增强梯度提升算法进行不平衡岩爆评估及其可解释性
我们开展了一项研究来评估梯度提升算法在岩爆评估中的潜力和稳健性,建立了一个变分自动编码器(VAE)来解决岩爆数据集的不平衡问题,并提出了一种针对基于树的集成学习的多级可解释人工智能(XAI)。我们从现实世界的岩爆记录中收集了537个数据,并选择了四个导致岩爆发生的关键特征。首先,我们使用数据可视化来深入了解数据的结构,并进行相关性分析以探索数据分布和特征关系。然后,我们建立了一个VAE模型来为由于类别分布不平衡而产生的少数类生成样本。结合VAE,我们比较和评估了六种最先进的集成模型,包括梯度提升算法和经典逻辑回归模型,用于岩爆预测。结果表明,梯度提升算法优于经典的单一模型,而 VAE 分类器优于原始分类器,其中 VAE-NGBoost 模型的结果最为理想。与针对不平衡数据集结合 NGBoost 的其他重采样方法(例如合成少数族群过采样技术 (SMOTE)、SMOTE 编辑最近邻 (SMOTE-ENN) 和 SMOTE-tomek 链接 (SMOTE-Tomek))相比,VAE-NGBoost 模型的效果最佳。最后,我们使用特征灵敏度分析、Tree Shapley 附加解释 (Tree SHAP) 和 Anchor 开发了一个多级 XAI 模型,以深入探索 VAE-NGBoost 的决策机制,进一步增强基于树的集成模型在预测岩爆发生方面的可靠性。
使用变异自动编码器生成波动率表面
这项研究对在指数股票市场的背景下对变量自动编码器(VAE)的利用进行了深入探索,这是期权定价的关键方面。此外,我们的研究还研究了有关现货价格爆发的神经网络作品的预测能力,并具有专门的现场模型,以预测基于现货动态的波动性表面的变化。通过VAE的全面数据处理和结构化,我们创建了一个模型,该模型能够从仅10点信息点生成准确且几乎无套的无动力表面。该模型也证明了在生成以前看不见的基本资产的波动表面方面的促进效率。将现货价格变化作为条件变量,我们成功地创建了一个强大的风险管理工具,能够预测各种未来情况的波动表面。
推荐系统中的变量自动编码器的调查
推荐系统已成为将人们与信息联系起来的重要工具。稀疏,复杂且快速增长的数据为传统推荐算法带来了新的挑战。为了克服这些挑战,已经提出了各种基于深度学习的建议算法。其中,基于变异的自动编码器(VAE)的推荐方法脱颖而出。vae s基于一个可信的概率框架,该框架适用于数据稀疏性,并且与其他基于深度学习的模型兼容以处理多模式数据。此外,vae s的深刻生成结构有助于以良好的方式进行贝叶斯推断。基于VAE的推荐算法已经引起了许多新型图形模型,并实现了有希望的性能。在本文中,我们进行了一项调查,以系统地总结了最近的基于VAE的推荐算法。总结了基于VAE的推荐算法的四个常用特征,并提出了基于VAE的建议算法的分类法。我们还确定了未来的研究指示,对推荐算法中VAE S的高级观点以及应用的应用,以激发推荐系统的VAE上的未来工作。
用于可植入脑机接口的脉冲神经网络解码器及其在 RISC-V 微控制器上的稀疏感知部署
摘要 — 可植入脑机接口 (BMI) 在运动康复和移动性增强方面大有可为,它们需要准确且节能的算法。在本文中,我们提出了一种用于可植入 BMI 的回归任务的新型脉冲神经网络 (SNN) 解码器。SNN 通过增强的时空反向传播进行训练,以充分利用其处理时间问题的能力。所提出的 SNN 解码器在离线手指速度解码任务中的表现优于最先进的卡尔曼滤波器和人工神经网络 (ANN) 解码器。解码器部署在基于 RISC-V 的硬件平台上,并经过优化以利用稀疏性。所提出的实现在占空比模式下的平均功耗为 0.50mW。在进行无占空比的连续推理时,它实现了每次推理 1.88 µ J 的能效,比基线 ANN 低 5.5 倍。此外,每次推理的平均解码延迟为 0.12 毫秒,比 ANN 实现快 5.7 倍。
分子设计的内核弹性自动编码器
我们介绍了内核弹性自动编码器(KAE),这是一种基于变压器架构的自我监管的生成模型,具有增强的分子设计性能。KAE采用了两个创新的损失函数:修改后的最大平均差异(M-MMD)和加权重建(L WCEL)。 与使用传统的kullback损失(vae的Leibler损失或标准的最大平均差异)相比,M-MMD损失显着改善了KAE的生成性能。 包括加权重建损失l wcel,Kae同时实现有效的生成和准确的重建,从而允许在现有生成方法中介于VAE和自动编码器之间中间的生成行为。 KAE的进一步进步包括与有条件生成的集成,在受限的优化中设定了新的最新基准测试。 此外, KAE已经证明了其在对接应用中产生具有良好结合亲密关系的分子的能力,如Autodock Vina和Glide分数所证明的那样,表现出优于培训数据集中所有现有的候选者。 除了分子设计之外,Kae还希望在广泛的应用中逐渐解决问题。KAE采用了两个创新的损失函数:修改后的最大平均差异(M-MMD)和加权重建(L WCEL)。与使用传统的kullback损失(vae的Leibler损失或标准的最大平均差异)相比,M-MMD损失显着改善了KAE的生成性能。包括加权重建损失l wcel,Kae同时实现有效的生成和准确的重建,从而允许在现有生成方法中介于VAE和自动编码器之间中间的生成行为。KAE的进一步进步包括与有条件生成的集成,在受限的优化中设定了新的最新基准测试。KAE已经证明了其在对接应用中产生具有良好结合亲密关系的分子的能力,如Autodock Vina和Glide分数所证明的那样,表现出优于培训数据集中所有现有的候选者。除了分子设计之外,Kae还希望在广泛的应用中逐渐解决问题。