XiaoMi-AI文件搜索系统
World File Search System胜科晶科Shine SAOC
“辅助服务”指 (1) 持牌发电厂、持牌发电厂/海水淡化厂或将其场所连接到输电系统或配电系统的其他人士可能需要不时提供的与该输电系统或整个系统的安全性和稳定性有关的服务;及 (2) 在 (i) 持牌输电系统运营商或持牌配电系统运营商与任何人士之间的协议或 (ii) 持牌发电厂或持牌发电厂/海水淡化厂与 PWP 之间的协议中规定的服务;
<全国读书推广日>基地领导朗读
2023 年 3 月 7 日 作者:参谋军士Braden Anderson 第 374 空运联队公共事务 在全国阅读推广日之际,第 374 空运联队的指挥官和其他管理人员最近为横田空军基地的儿童保育设施 Yume 儿童发展中心揭幕。孩子们。 这个周年纪念日是由国家教育协会于1998年设立的,是一个向孩子们传达阅读乐趣的日子。之所以选择3月2日,是因为这是图画书作者苏斯博士的生日。 横田图书馆一直参与国防部福利服务管理局的暑期阅读计划,该计划旨在鼓励年轻人在暑假期间养成阅读的习惯。允许日本员工使用图书馆。
日美首脑会谈成果文件(太空部分)
我们的全球伙伴关系还延伸到太空,美国和日本在探索太阳系和重返月球方面处于领先地位。我们欢迎今天签署关于加压月球车探索月球表面的实施安排。根据协议,日本将提供并维护一辆加压月球车,而美国则计划在未来的阿尔特弥斯任务中为日本宇航员分配两次登月机会。两位领导人宣布了一个共同目标,即在满足关键基准的情况下,日本宇航员将成为在未来的阿尔忒弥斯 (Artemis) 任务中首位登陆月球的非美国公民。为实现这一目标,美国和日本计划深化在宇航员培训方面的合作,同时管理此类富有挑战性和启发性的月球任务带来的风险。我们还宣布在高超音速滑翔飞行器(HGV)和其他导弹的低地球轨道(LEO)搜索和跟踪星座方面开展双边合作,包括与美国工业界的潜在合作。美日联合领导人声明 面向未来的全球合作伙伴 开拓太空新领域 我们的全球伙伴关系延伸到太空,美国和日本正在引领探索太阳系和重返月球的道路。今天,我们欢迎签署月球表面探索实施协议,根据该协议,日本计划提供并维持加压月球车的运行,而美国计划在未来的阿尔特弥斯任务中为日本分配两次宇航员登月机会。 两国领导人宣布了一个共同目标,即假设实现重要基准,日本国民将成为未来阿尔特弥斯任务中第一位登陆月球的非美国宇航员。美国和日本计划深化宇航员培训方面的合作,以促进这一目标的实现,同时管理这些具有挑战性和鼓舞人心的月球表面任务的风险。 我们还宣布在低地球轨道探测和跟踪星座方面进行双边合作,用于高超音速滑翔飞行器等导弹,包括与美国工业界的潜在合作。
科克伦
神经内分泌肿瘤 (NET) 有时也称为类癌肿瘤,是一组源自内分泌(激素)和神经系统细胞的异质性恶性肿瘤(癌症)。根据美国国家癌症研究所的监测、流行病学和最终结果 (SEER) 18 登记处的数据,估计神经内分泌肿瘤 20 年总患病率为 171,321 例,每年年龄调整后的发病率为每 100,000 人 6.98 例(Dasari 2017)。一项基于人群的研究发现,1973 年至 2012 年间,神经内分泌肿瘤的发病率增加了 6.4 倍(Dasari 2017)。NET 在高龄患者中更常见,65 岁或以上患者的发病率为每 100,000 人 25 例。约 61.0% 的 NET 源自胃肠道或胰腺( Lawrence 2011 ),因此这些肿瘤被称为胃肠胰 NET(GEP-NET)。原发性 NET 的其他部位包括肺、甲状腺、卵巢、宫颈、垂体和肾上腺( Hallet 2015 )。
2024年侦查科技与鉴识科学研讨会议程表
海报論文发表林韦志杨筑安杨筑安赖欣宜易哲安陈国豪邓珮琳徐培文侯儒君胡瑄耘王乔立苏正宪苏志文黄兆清洪翊芸Wee Beng Lim 陈淯圣郭哲玮林子玮林柏廷宋泓葰柯虹瑩林政宏林奕全张馨呂宗谚林弘杰陈家维蔡奇男陈瑜轩孙德娟林子桓邱景徽陈祺蔡世国谢立伟翁颖信苏柏豪陈韦佑王升钧洪孟君胡家豪陈羽蓁林炜翔胡政嘉胡政嘉林文元许倬宪余滋雅褚祥蕴洪晨玮许嘉峻陈冠玮葉怡伶吴家森慧麗Mintra Phochanamanee 吴宗原
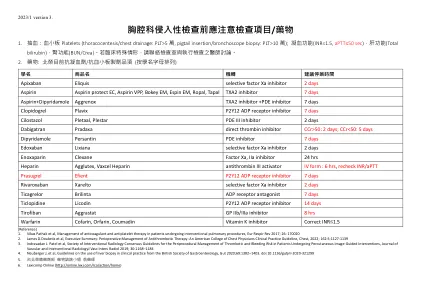
胸腔科侵入性检查前应注意检查项目/药物
[参考] 1。Vikas Pathak等人,接受介入肺部程序的患者的抗凝剂和抗血小板治疗的管理,Eur Respir Rev 2017; 26:170020 2。James D.Douketis等人,执行摘要:抗血栓疗法的围手术期管理:美国胸部医师学院临床实践指南,胸部,2022年; 162:5:1127-1139 3。Indravadan J. Patel等人,介入放射学共识学会指南,围骨围骨治疗的血栓形成和出血风险,接受经皮图像引导的患者,血管和介入放射学杂志杂志,介入介绍性和介入的放射性放射学指南。 30:1168–1184 4。neuberger J等人,关于英国胃肠病学会临床实践中使用肝活检的指南,直肠2020; 69:1382–1403。doi:10.1136/gutjnl-2020-321299
在临界状态下关联非厄米和厄米量子系统
我们展示了三种类型的变换,它们在临界状态下建立了厄米和非厄米量子系统之间的联系,可以用共形场论 (CFT) 来描述。对于同时保留能量和纠缠谱的变换,从纠缠熵的对数缩放中获得的相应中心电荷对于厄米和非厄米系统都是相同的。第二种变换虽然保留了能量谱,但不保留纠缠谱。这导致两种类型的系统具有不同的纠缠熵缩放,并导致不同的中心电荷。我们使用应用于自由费米子情况的膨胀方法来展示这种变换。通过这种方法,我们证明了中心电荷为c = −4的非厄米系统可以映射到中心电荷为c = 2的厄米系统。最后,我们研究了参数为φ →− 1 /φ的斐波那契模型中的伽罗瓦共轭,其中变换既不保持能量谱也不保持纠缠谱。我们从纠缠熵的标度特性证明了斐波那契模型及其伽罗瓦共轭与三临界Ising模型/三态Potts模型和具有负中心电荷的Lee-Yang模型相关联。