XiaoMi-AI文件搜索系统
World File Search System积分的
EU化学化学策略可持续性会议EU化学化学策略可持续性会议
•塑料闪光（松散的塑料闪光）是触手可及的混合物•2023年10月17日的产品不需要召回或撤回（第2段。6.）•出售在工业场所使用的闪光/spm4a）•用材料制成的无机闪光（例如玻璃，金属），天然，可生物降解或在水中可溶（不在范围之外）•如果固定在文章上的闪光取决于闪光是文章的组成部分，还是装饰功能是次要的（超出范围）或纯粹的装饰功能，而不是积分的功能，而不是整体•珠子和亮片•螺纹和亮片打算呈螺纹或缝制作品或缝制作品（远离艺术品）。•用作化妆品产品的松散塑料闪光以及包含闪光的化妆品具有特定的过渡期。6。
深低温下 FDSOI 器件的 TCAD 模拟
摘要 — 本文证明了在深低温下 FDSOI 器件 TCAD 模拟的可行性。为此，麦克斯韦-玻尔兹曼载流子统计被具有 3D 态密度的费米-狄拉克积分的解析近似所取代。通过求解二维泊松方程来研究器件静电，而使用漂移扩散模型模拟传输。我们探讨了温度对线性和饱和区器件性能的影响以及短沟道效应的影响，这些影响考虑了各种栅极和间隔物长度、室温和深低温。最后，将得到的结果与一些实验数据进行了比较，强调了 TCAD 模拟在提供器件物理和性能见解方面的作用。关键词 — 低温电子学、FDSOI、TCAD 模拟
亚洲发展最快的律师事务所
5.5 个公共 CPD 积分（第一天 3 个公共 CPD 积分，第二天 2.5 个公共 CPD 积分）实践领域：企业/商业 | 培训级别：一般希望获得 CPD 积分的参与者必须严格遵守 CPD 指南中规定的出勤政策。对于此活动，这包括在活动的每一天在网络研讨会开始时登录并在网络研讨会结束时注销，并且活动的每一天离开网络研讨会的任何部分的时间不得超过 15 分钟。参与者在活动的每一天都可以获得公共 CPD 积分，只要他们严格遵守出勤政策。不遵守出勤政策的参与者将无法获得参加活动的 CPD 积分。请参阅 http://www.sileCPDcentre.sg 了解更多信息。
M. SC。物理学（具有材料科学专业化） MCA
单元2特殊功能08小时的特殊功能定义；为整体顺序JN（X）的Bessel函数生成函数; Hermite多项式；为隐士多项式生成功能；特殊功能在物理学中的应用。单元-3傅里叶系列10小时周期功能； Euler Fourier公式； Dirichlet条件；半范围傅立叶系列；间隔的变化； Parseval的身份；在物理学中，很少有傅立叶串联振动串，RLC电路和其他一般应用的应用。单元4积分转换12小时的积分变换；拉普拉斯变换；拉普拉斯变换的特性；逆拉环变换；衍生物和积分的拉普拉斯变换；拉普拉斯方程 - 应用于静电场。
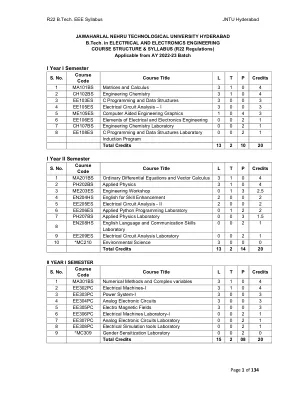
R18 B.Tech。 MME教学大纲Jntu Hyderabad 1
编写一组线性方程的矩阵表示，并分析方程系统的解决方案查找特征值和特征向量使用正交转换将二次形式减少到规范形式。在平均值定理上求解应用程序。使用beta和伽马函数评估不正确的积分找到两个具有/没有约束的变量的功能的极端值。评估多个积分，并将概念应用到查找区域，量ITUME-I：矩阵10 L矩阵的矩阵等级和正常形式的矩阵等级，正常形式，与juss-jordan方法的非单明性矩阵相反，高斯 - jordan方法，线性方程系统：均匀和非同性方程式的求解系统和非良好方程式的求解方法。UNIT-II: Eigen values and Eigen vectors 10 L Linear Transformation and Orthogonal Transformation: Eigenvalues, Eigenvectors and their properties, Diagonalization of a matrix, Cayley-Hamilton Theorem (without proof), finding inverse and power of a matrix by Cayley-Hamilton Theorem, Quadratic forms and Nature of the Quadratic Forms, Reduction of正交转换通过正交转换到规格形式的二次形式。单位-III：微积分10 L平均值定理：Rolle的定理，Lagrange的平均值定理，其几何解释和应用，Cauchy的平均值定理，Taylor的序列。确定积分的应用在评估曲线旋转的表面区域和体积（仅在笛卡尔坐标中），不当积分的定义：beta和伽马功能及其应用。单元IV：多变量演算（部分分化和应用）10 L极限和连续性的定义。部分分化：Euler的定理，总导数，Jacobian，功能依赖性和独立性。应用程序：使用拉格朗日乘数方法的两个变量和三个变量的功能的最大值和最小值。
微积分导论 - 哈佛数学系
0.1。本课程是微积分的入门课程，于 2011-2014 和 2020-2021 年在哈佛大学教授。虽然不需要之前接触过微积分，但需要具备几何和代数等基本的微积分预备技能。即使你以前学过一些微积分，像这样的大学单变量微积分课程也会让你对这个主题有更深入、更概念性的理解。它让你看到数学理论的美丽和优雅，并欣赏它的应用。虽然概念和应用都很重要，但技能的掌握也是关键。尤其是在一个新领域的第一步，你必须专注于技能。幸运的是，程序比洞察力更容易学习和教授，洞察力需要更多的时间，因为它需要经验和连接点的能力，看到相似之处、模式和提出问题的能力。
泰米尔纳德邦政府公报
单元I数学物理学维度分析：微分方程（普通和部分） - 方程顺序 - 梯度，发散，卷曲和laplacian的表达式 - 矢量代数和矢量计算 - 高斯分歧定理 - 格林的定理 - Stokes的定理。矩阵：Cayley - 汉密尔顿定理，矩阵倒数 - 特征值和特征向量。多项式：Hermite，Bessel和Legendre功能。特殊功能：beta和伽马功能。概率：基本概率理论 - 随机变量 - 二项式 - 泊松和正态分布。复杂变量：分析函数 - 奇异点 - 库奇的积分定理和公式-Taylor's和Laurent的扩展，杆子，残基的计算以及积分的评估。积分变换：傅立叶系列和傅立叶变换及其属性。
支持 API 的数字生态系统 - 德勤
随着 API 的出现，传统的联盟组建方式（实体资产联盟）正在让位于“新时代”数字联盟，这种联盟的参与条款清晰、自动化且可扩展。一家全球航空联盟中，多家航空公司 (5) 共享实体资源，从而为客户提供更广泛的目的地，以及收集和使用这些航空公司的里程积分的选项。然而，随着数字化和基于 API 的联盟的不断增加，客户可以访问不同的资源，参与和收入分享条款可以实现自动化。例如，一家在线旅行聚合器的公开 API 实现了跨多个合作伙伴的海量数据集成。这些合作伙伴包括竞争航空公司和数千家其他服务提供商，因此当合作伙伴加入时，他们会寻求更多的边际效益。