XiaoMi-AI文件搜索系统
World File Search System积分的
USACE LEED-NC 2009 未注册项目提交
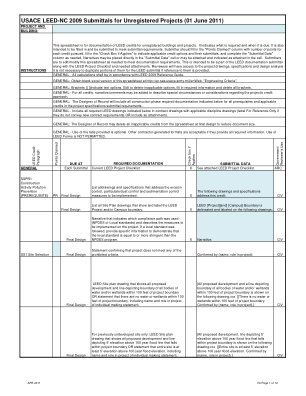
此电子表格用于记录未注册建筑和项目的 LEED 积分。它表明需要什么以及何时到期。它还旨在填写并提交以满足提交要求。提交者应在“已申请积分”列中填写每个积分的积分数，填写“如果适用则勾选”以指示适用的积分选项及其提交，并根据需要完成“提交数据”列。叙述可以直接放在“提交数据”单元格中，也可以附加并在单元格中指示为附加。提交者应根据需要编辑/修改此电子表格以满足文档要求。这旨在与 LEED 项目清单和所需附件一起成为 LEED 文档提交的一部分。审阅者将有权查看项目图纸、规格和设计分析 - 如果提供了参考，则无需在 LEED 提交中复制其中的部分内容。
计算机科学与工程学士学位 (人工智能与...) 课程计划
课程成果： 1）分析序列或级数的性质（收敛或发散）。 2）应用中值定理研究物体的运动。 3）用积分计算面积、体积、质量和重心。 4）应用多元微积分研究多元函数的性质。 5）理解微分方程的概念及其应用 课程内容： 模块一：序列和级数：实数序列、级数、比率和根测试。 模块二：单变量函数微积分：极限、连续性和可微性的回顾。 中值定理：罗尔定理、拉格朗日定理、柯西定理、带余数的泰勒定理、不定式、曲率、曲线追踪。积分学基本定理、积分学平均值定理、定积分的计算、在旋转体面积、长度、体积和表面积中的应用、不定积分：Beta 函数和 Gamma 函数、积分符号下的微分。
佐治亚大学系统概述影响核心课程
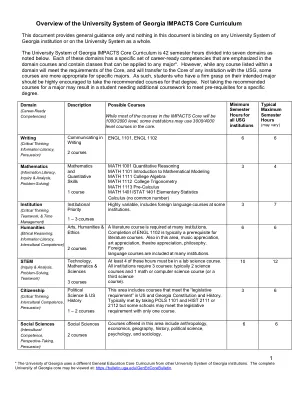
选择数学域名的数学选择，没有USG学校可以要求学生在任何数学领域课程中读取特定课程。无论学生参加哪个数学课程，它都必须计入满足数学领域要求的满足，并且必须计入毕业。但是，应该建议学生参加最适合其预期专业的数学课程。，数学1001或数学1101是特定专业的默认建议，具有强大的数学兴趣和能力的学生可能会选择服用数学1111，但是建议大多数学生参加数学1001，MATH 1101或MATH/STAT/STAT 1401。还应注意，Math 1111旨在为学生做好准备，这对于不会在学位课程中参加微积分的学生来说，这不是最好的课程。
艺术状态：CCS Technologies 2024
•我们的氢生产技术没有直接排放，并且达到了超低碳强度，比CCS（ATR+CCS）的最先进的自动热改革低15-20％。•CO 2的捕获固有地内置在过程设计中，捕获超过99.5％，同时避免使用有毒化学物质或能源密集型过程。•结合了商业证明的氢生产过程的优势，以可靠地提供清洁和负担得起的能源。•利用尾巴气体的氧气燃烧来提供改革和热积分的热量，使高效的循环具有5-7％的热效率增益，而基准ATR+CCS。•结合在一起，与目前市场上所有公用事业规模的氢技术相比，8RH 2的平整成本无与伦比。•轻松地与氨循环技术集成，以实现超低碳氨的产生，该氨可以作为商品交易或用于更容易的H 2运输。
艺术状态：CCS Technologies 2024
•我们的氢生产技术没有直接排放，并且达到了超低碳强度，比CCS（ATR+CCS）的最先进的自动热改革低15-20％。•CO 2的捕获固有地内置在过程设计中，捕获超过99.5％，同时避免使用有毒化学物质或能源密集型过程。•结合了商业证明的氢生产过程的优势，以可靠地提供清洁和负担得起的能源。•利用尾巴气体的氧气燃烧来提供改革和热积分的热量，使高效的循环具有5-7％的热效率增益，而基准ATR+CCS。•结合在一起，与目前市场上所有公用事业规模的氢技术相比，8RH 2的平整成本无与伦比。•轻松地与氨循环技术集成，以实现超低碳氨的产生，该氨可以作为商品交易或用于更容易的H 2运输。
aaos 2025 - 展览会简介
与其他公司合并、被收购或收购过其他公司的公司可以使用最有利的公司的展览历史，但不能将多家公司的展览历史合并起来以计算优先积分。应以书面形式通知 AAOS 公司之间的收购或合并已经完成，以及此变更的生效日期。申请转移优先积分的公司必须与参展公司有直接关系才能继承这些优先积分。直接相关公司应定义为由其他公司的子公司全资拥有或与其他公司合并的公司。仅当展示类似产品线时才会授予优先积分。仅在 AAOS 自行决定的范围内，将产品、产品线、某些技术或某些资产出售给其他公司才会被视为转移优先积分。所有优先积分交易请求必须以书面形式提交至 exhibits@aaos.org，并由母公司或子公司书面确认。
三年制飞机文凭课程... - Bteup
1. 代数 (i) 方程理论和根的对称函数。(ii) 二项式、对数和指数级数、一般指数和对数级数（修订版）。(iii) 复数及其在工程问题中的应用。(iv) 矢量及其图形表示矢量的数学运算。(v) 矩阵和行列式（基本概念）。 2. 三角学 (i) 反圆函数。(ii) 德莫维尔定理及其应用。 3. 微分学：(i) 求函数微分系数导数的方法。(ii) 函数的微分。(iii) 对数微分。(iv) 逐次微分。(v) 偏微分。(vi) 切线和法线的应用。(vii) 最大值和最小值 4. 积分学 (i) 不定积分的方法。 (ii) 代换积分。 (iii) 分部积分。 (iv) 积分在圆柱体、圆锥体和球体的表面积、面积和体积计算中的应用。
量子力学和量子场中的 5 路径积分...
路径积分图景之所以重要，有两个原因。首先，它提供了量子力学的另一种补充图景，其中经典极限的作用显而易见。其次，它为研究微扰理论不充分或完全失效的领域提供了一条直接途径。在量子力学中，解决此类问题的标准方法是 Wentzel、Kramers 和 Brillouin 的 WKB 近似。然而，将 WKB 近似推广到量子场论是极其困难的（甚至是不可能的）。相反，费曼路径积分的非微扰处理（在量子力学中等同于 WKB）可以推广到量子场论中的非微扰问题。在本章中，我们将仅对玻色子系统（如标量场）使用路径积分。在后续章节中，我们还将对路径积分进行全面的讨论，包括它在费米子场、阿贝尔和非阿贝尔规范场、经典统计力学和非相对论多体系统中的应用。