XiaoMi-AI文件搜索系统
World File Search SystemZX -DIAGRAM的相互作用的几何形状 - 滴
量子计算是一种计算模型,其中数据存储在受量子物理定律控制的粒子状态下。该理论已经足够确定,可以设计其应用程序从公共和私人参与者那里收集利益的量子算法[29,31,17]。量子对象的基本属性之一是具有双重解释。在第一个中,量子对象被理解为粒子:空间中的确定,局部点,与其他粒子不同。光可以被视为一组光子。在另一种解释中,该对象被理解为波浪:它在空间中“扩散”,可能具有干扰。这是将光解释为电磁波的解释。计算的标准模型使用量子位(Qubits)来存储信息和量子电路[30],以描述带有量子门的量子操作,这是布尔门的量子版本。尽管用于量子计算的普遍模型,但仅以直观的方式给出了量子电路的操作语义。量子电路被理解为某种顺序的低级装配语言,其中量子门是不透明的黑盒。特别是,量子电路本身并不具有任何形式的操作语义,从而引起抽象的推理,方程理论或有充分的重写系统。从表示的角度来看,量子电路是线性操作员的张量和应用的字面描述。这些可以用历史矩阵解释[30]或更近期的总计语义[1,6]来描述这些 - 这可以是
idris 2:实践中的定量类型理论 - 滴
依赖类型允许我们精确地表达函数打算做的事情。定量类型理论(QTT)的最新工作以线性性扩展了相关类型系统,也可以精确表达何时运行函数。这是很有希望的,因为它建议对资源使用协议进行设计和推理的能力,例如我们在分布式和并发编程中可能会发现的,其中通信渠道的状态在整个程序执行过程中会发生变化。到目前为止,还没有使用这些想法来实验的完整编程语言。idris 2是依赖类型的语言IDRI的新版本,具有基于QTT的新核心语言,支持线性和依赖类型。在本文中,我们介绍了IDRIS 2,并描述了QTT如何影响其设计。我们在实践中举例说明了QTT的好处,包括:在运行时,类型级别删除哪些数据;并且,在类型系统中进行资源跟踪,从而导致类型和会话类型的类型安全程序编程。
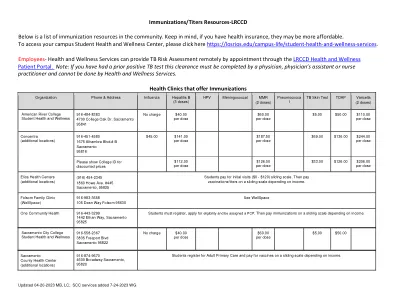
您可能需要额外的滴度和/或测试...
• IGRA(干扰素伽玛释放试验)血液测试(Quantiferon-Gold 或 T-Spot)或(2)步结核病皮试 • IGRA 血液测试是首选,因为只需去实验室抽血 1 次;并且测试更客观。 • (2) 步结核病皮试包含 2 个不同的结核病皮试,这 2 个测试间隔 1-3 周内完成,但读数间隔不得少于 7 天。这就需要 4 次单独去诊所进行两次测试并读取读数。 • 这是某些学院对学生的年度要求。一旦您进行了基线 IGRA 血液测试或(2)步结核病皮试,您可能只需要每年完成(1)步结核病皮试 - 前提是它要在前一年测试到期之前完成。IGRA 测试(Quantiferon-Gold 或 T-Spot)也可以满足年度要求。
免疫接种/滴度资源-LRCCD
员工 - 卫生与保健服务部门可通过 LRCCD 卫生与保健患者门户网站预约远程提供结核病风险评估。注意:如果您之前的结核病检测结果呈阳性,则此检查必须由医生、医生助理或执业护士完成,卫生与保健服务部门不能完成此检查。
您可能需要额外的滴度和/或测试...
• IGRA(干扰素伽玛释放试验)血液测试(Quantiferon-Gold 或 T-Spot)或(2)步结核病皮试 • IGRA 血液测试是首选,因为只需去实验室抽血 1 次。 • (2) 步结核病皮试包含 2 个不同的结核病皮试,间隔 1-3 周完成。结核病测试由医疗保健提供者 (HCP) 进行,然后在 48-72 小时后读取。这需要 4 次单独去诊所进行测试和读取。 • 这是一项年度要求。一旦您进行了基线 IGRA 血液测试或(2)步结核病皮试,您可能只需要每年完成(1)步结核病皮试 - 前提是该测试在前一年测试到期之前完成。IGRA 测试(Quantiferon-Gold 或 T-Spot)也可以满足年度要求。
SOK:零知识范围证明 - 滴
零知识范围证明(ZKRP)允许供奉献者说服验证者,秘密值在给定的间隔中。ZKRP有许多应用程序:从匿名凭证和拍卖到加密货币的机密交易。同时,文献中存在众多ZKRP结构,每个构建都有自己的权衡。在这项工作中,我们将围绕ZKRP的知识系统化。我们根据基础建筑技术创建了现有构造的分类,并总结了它们的属性。我们在属性和效率水平方面提供了方案之间的比较,并构建了一个指南,以帮助选择适当的ZKRP来满足不同的应用要求。最后,我们讨论了许多有趣的开放研究问题。
组装多室细胞模仿液滴
细胞模仿是多室的系统,可再现自然细胞的结构和功能。它们代表着迈向智能,自动和模块化寿命系统的重要一步。[1]可以量身定制细胞模仿,以有效地执行多种生化任务,并且可以设计用于与天然细胞的接口,从而弥合材料科学与生物学之间的差距。[2]基本的细胞模拟设计由一个主要的室(例如聚合物或脂质囊泡)组成,该室包含了各种结构和功能成分,包括子组门,细胞骨架,核酸,质子酸,蛋白质,蛋白质和酶。然而,随着组件的复杂性的增加,一个主要的障碍物成为复制真核细胞中发现的多门特征的能力,同时保持对
跨度程序和量子时间复杂性 - 滴
跨度程序是量子计算的重要模型,因为它们与量子查询和空间复杂性的对应关系。虽然从SPAN程序获得的量子算法的查询复杂性是充分理解的,但通常不清楚如何以时间效率的方式实现某些独立的操作。在这项工作中,我们证明了量子时间复杂性的类似连接。,我们展示了如何将F对于时间复杂性t t的足够结构结构的量子算法转换为f的跨度程序,从而将其汇编回到f的量子算法中,并使用时间复杂性e O(t)。这表明,对于具有时间效率实现的算法衍生的跨度程序,我们可以在实现跨度程序时保留时间效率,这意味着SPAN程序捕获时间,查询和空间复杂性,并且是量子算法的完整模型。能够以保持时间复杂性的方式将量子算法转换为跨度程序的一个实际优势是,跨度程序构成非常好。我们通过通过跨度程序组成或功能来改善Ambainis的可变时间量子搜索结果来证明这一点。