XiaoMi-AI文件搜索系统
World File Search System线性化
具有背景非线性校正的数字射频发射机
I. 引言 近年来，数字射频 (RF) 发射器 (TX) 越来越受欢迎。在数字域中实现发射功能有许多优势，例如，可以省去模拟模块，如可变增益放大器、失调消除数模转换器 (DAC) 和预驱动器。RF 发射器（无论是模拟还是数字）面临的最大挑战是线性度和效率之间的权衡，这反过来又导致了许多线性化技术的出现。由于芯片温度会随 TX 输出功率而有很大变化，因此必须实时继续线性化；也就是说，如果前台校准技术试图校正高度非线性的输出级，则它们会被证明是不够的。本文介绍了一种新的 TX 线性化方法，可在后台校正静态和动态非线性。校正的有效性允许设计 DAC 以实现具有几乎任意积分非线性 (INL) 的最大效率。以宽带码分多址 (WCDMA) 标准为例，简单、紧凑的架构提供了迄今为止报告的最高效率。该发射器采用 28 纳米标准 CMOS 技术实现，可提供 + 24.1 dBm 的功率，相邻信道功率比 (ACPR) 为 − 35.4 dB，总效率为 50%。
b'摘要。本文提出了将对称密码代数方程转化为QUBO问题的方法。将给定方程f 1 ，f 2 ，... ，fn转化为整数方程f \xe2\x80\xb2 1 ，f \xe2\x80\xb2 2 ，... ，f \xe2\x80\xb2 n后，对每个方程进行线性化，得到f \xe2\x80\xb2 lin i = lin ( f \xe2\x80\xb2 i )，其中lin表示线性化运算。最后，可以得到 QUBO 形式的问题，即 f \xe2\x80\xb2 lin 1 2 + \xc2\xb7 \xc2\xb7 \xc2\xb7 + f \xe2\x80\xb2 lin n 2 + Pen ，其中 Pen 表示在方程线性化过程中获得的惩罚，n 是方程的数量。在本文中，我们展示了一些分组密码转换为 QUBO 问题的示例。此外，我们展示了将完整的 AES-128 密码转换为 QUBO 问题的结果，其中等效 QUBO 问题的变量数量等于 237,915，这意味着，至少在理论上，该问题可以使用 D-Wave Advantage 量子退火计算机解决。不幸的是，很难估计这个过程所需的时间。'
b'摘要。本文提出了将对称密码代数方程转化为QUBO问题的方法。将给定方程f 1 ，f 2 ，... ，fn转化为整数方程f \xe2\x80\xb2 1 ，f \xe2\x80\xb2 2 ，... ，f \xe2\x80\xb2 n后，对每个方程进行线性化，得到f \xe2\x80\xb2 lin i = lin ( f \xe2\x80\xb2 i )，其中lin表示线性化运算。最后，可以得到 QUBO 形式的问题，即 f \xe2\x80\xb2 lin 1 2 + \xc2\xb7 \xc2\xb7 \xc2\xb7 + f \xe2\x80\xb2 lin n 2 + Pen ，其中 Pen 表示在方程线性化过程中获得的惩罚，n 是方程的数量。在本文中，我们展示了一些分组密码转换为 QUBO 问题的示例。此外，我们展示了将完整的 AES-128 密码转换为 QUBO 问题的结果，其中等效 QUBO 问题的变量数量等于 237,915，这意味着，至少在理论上，该问题可以使用 D-Wave Advantage 量子退火计算机解决。不幸的是，很难估计这个过程所需的时间。'
在智能网格的背景下，用可再生能源控制AC/DC微电网：包括辅助服务和电动移动性
4控制策略77 4.1简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。77 4.1.1模型简介。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。78 4.2超级隔离器子类型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。79 4.2.1超级隔离器模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。80 4.2.2非最低相位问题。。。。。。。。。。。。。。。。。。。。。。。。80 4.2.3控制诱导的时间尺度分离。。。。。。。。。。。。。。。。。。。。82 4.2.4超级电容器控制应用程序。。。。。。。。。。。。。。。。。。。。。。86 4.2.5零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。87 4.2.6参考计算。。。。。。。。。。。。。。。。。。。。。。。。。。。。。89 4.3电池子系统。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。91 4.3.1电池模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。92 4.3.2反馈线性化。。。。。。。。。。。。。。。。。。。。。。。。。。。。93 4.3.3零动力学分析。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 94 4.4 PV数组子系统。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 95 4.4.1 PV数组模型。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 96 4.4.2反馈线性化。 。 。 。 。 。93 4.3.3零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。94 4.4 PV数组子系统。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。95 4.4.1 PV数组模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。96 4.4.2反馈线性化。。。。。。。。。。。。。。。。。。。。。。。。。。。。96 4.4.3零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。97 4.5 DC负载子系统。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。98 4.5.1 DC负载模型。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。98 4.5.1 DC负载模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。98 4.5.2反向替代控制。。。。。。。。。。。。。。。。。。。。。。。。。。。。。99 4.5.3零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。101 4.6再生制动子系统。。。。。。。。。。。。。。。。。。。。。。。。。。。102 4.6.1再生制动模型。。。。。。。。。。。。。。。。。。。。。。。。。。103 4.6.2再生制动控制应用。。。。。。。。。。。。。。。。。104 4.6.3零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。105 4.6.4参考计算。。。。。。。。。。。。。。。。。。。。。。。。。。。。。106 4.7 AC网格连接。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 107 4.7.1 AC网格模型。106 4.7 AC网格连接。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。107 4.7.1 AC网格模型。107 4.7.1 AC网格模型。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。107 4.7.2反馈线性化。。。。。。。。。。。。。。。。。。。。。。。。。。。。109 4.7.3零动力学分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。109 4.7.4 PLL同步。。。。。。。。。。。。。。。。。。。。。。。。。。。。。110 4.8系统互连。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。111 4.8.1直流总线。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。111 4.8.2分层控制结构。。。。。。。。。。。。。。。。。。。。。。。。112 4.8.3预序。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。113 4.8.4稳定性分析。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。113
瞬时不稳定性和反应性模式在扩散 -
传统上，关于反应扩散和趋化系统模式形成的研究集中在渐近稳定性上，以解释模式的出现。在[11]中，作者分析了线性化系统的渐近趋化性扩散不稳定产生的模式的现象学，并研究了趋化项的不同作用：增强已经存在的图林不稳定或促进稳定同质平衡模型的不稳定发作时，是在增强稳定的不稳定的过程中。在该论文中，作者研究了雅各布在没有扩散的情况下的初始瞬态不稳定（如其反应性所检测到）是否仍然是线性化系统渐近不稳定性的必要条件，例如相应的纯扩散模型。
使用 K. lactis 蛋白质表达试剂盒进行蛋白质表达 - pKLAC2 的线性化用于 K. lactis 的整合转化。| NEB
剩余的 pKLAC2 载体 DNA。克隆的基因必须不含 SacII 位点（或 BstXI 位点，如果用 BstXI 消化）才能产生正确的表达片段。无需从剩余的 pKLAC2 载体 DNA 中纯化表达片段
Authenticase M0689手册
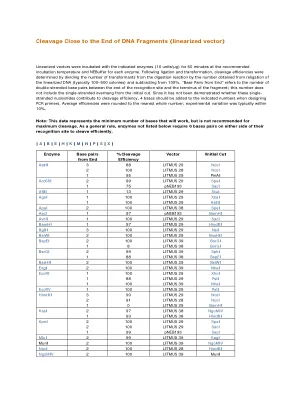
线性化载体与指定的酶（10单位/µg）在建议的孵化温度下60分钟，每种酶为星云孵育60分钟。在连接和转化后，通过将转化子与消化反应的数量除以从线性化DNA的宗教（通常为100-500个菌落）获得的数量来确定裂解效率，并从100％中减去。“从末端到基本对”是指识别位点末端和片段末端之间的双链基对数的数量；该数字不包括初始切割中的单链悬垂。由于尚未证明这些单链核苷酸是否有助于切割效率，因此在设计PCR引物时应将4个碱基添加到指定的数字中。平均效率被四舍五入到最接近的整数；实验变化通常在10％以内。
通过老化的意识操作提高电池储能系统的寿命盈利能力
锂离子细胞由于多种细胞内衰老效应而导致降解，这可以显着影响电池能量储能系统（BESS）的经济性。由于降解率取决于外部应力因素，例如电荷，电荷/放电率和周期深度，因此可以通过操作策略直接影响它。在此贡献中，我们提出了一个模型预测控制（MPC）框架，用于设计老化的意识操作策略。通过模拟数字双胞胎上的整个BESS寿命，可以基准测试不同的老化意识优化模型，并且可以确定老化成本的最佳价值。在案例研究中，研究了通过套利交易在EPEX现场盘中电力市场上通过套利交易的应用。为此，提出了用于日历的线性化模型和磷酸锂细胞的环状容量损失。结果表明，与基于电池系统的成本选择老化成本相比，使用MPC框架来确定最佳的老化成本可以显着提高BES的寿命盈利能力。此外，与基于能量吞吐量的基于能量吞吐量的老化成本模型相比，使用线性化日历降解模型时，能量套利的生命周期利润可以增加24.9％，使用线性化日历和环状降解模型时，可以增加24.9％。通过检查2019年至2022年的价格数据，该案例研究表明，批发电力市场的价格和价格波动的最新上涨导致可实现的终身利润大幅增加。