XiaoMi-AI文件搜索系统
World File Search System通过特征向量联合对齐实现 P300 脑机接口的迁移学习
摘要 — 本文介绍了一种新的迁移学习方法,即群组学习,它可以联合对齐多个域(多对多),以及一种扩展方法,即快速对齐,它可以将任何其他域与先前对齐的域组对齐(多对一)。在脑机接口 (BCI) 数据上评估了所提出的组对齐算法 (GALIA),并研究了该算法的最佳超参数值以了解分类性能和计算成本。使用了六个公开的 P300 数据库,包含来自 177 个受试者的 333 个会话。与传统的针对特定受试者的训练/测试流程相比,群组学习和快速对齐均显著提高了分类准确率,但临床受试者的数据库除外(平均改进:2.12±1.88%)。GALIA 利用循环近似联合对角化 (AJD) 来找到一组线性变换,每个域一个,联合对齐所有域的特征向量。群组学习实现了多对多迁移学习,同时不会损害非临床 BCI 数据的分类性能。快速对齐进一步扩展了任何未见域的群组学习,从而允许具有相同属性的多对一迁移学习。前一种方法使用来自先前受试者和/或会话的数据创建单个机器学习模型,而后一种方法利用训练后的模型来处理未见域,无需进一步训练分类器。
理解和利用过程张量的内在联系
过程张量矩阵积算子 (PT-MPO) 能够对空前广泛的开放量子系统进行精确的数值模拟。通过以 MPO 形式表示环境影响,可以使用已建立的算法对其进行有效压缩。压缩的 PT-MPO 内键的维度可以看作是环境复杂性的指标。在这里,我们表明,内键本身(而不仅仅是其维度)具有具体的物理意义:它们表示全环境刘维尔空间的子空间,该子空间承载着可能对后续开放量子系统动力学影响最大的环境激发。这种联系可以用有损线性变换来表示,其伪逆有助于提取环境可观测量。我们通过提取中心自旋问题的环境自旋、耦合到两个引线的量子系统的电流、从量子发射器发射到结构化环境中的光子数量以及驱动非马尔可夫量子系统中总吸收能量在系统、环境和相互作用能量项中的分布来证明这一点。数值测试进一步表明,不同的 PT-MPO 算法将环境压缩到相似的子空间。因此,PT-MPO 内部键的物理解释既提供了概念上的理解,也使新的实际应用成为可能。
近距离摄影测量
ADC 模拟数字转换器 AGC 自动增益控制 ASCII 美国信息交换标准代码 ASPRS 美国摄影测量与遥感协会 BRDF 双向反射分布函数 CAAD 计算机辅助建筑设计 CAD 计算机辅助设计 CAM 计算机辅助制造 CCD 电荷耦合器件 CCIR 国际无线电咨询委员会 (Comité consultatif international pour la radio) CD-ROM 光盘 - 只读存储器 CID 电荷注入装置 CIE 国际照明委员会 (Commission Internationale de l’Éclairage) CIPA 国际建筑摄影测量委员会 (Comité International de Photogrammétrie Architecturale) CMM 坐标测量机 CMOS 互补金属氧化物半导体 CT 计算机断层扫描、断层摄影 CTF 对比度传递函数 DAGM 德国模式识别协会 (Deutsche Arbeitsgemeinschaft für Mustererkennung) DCT 离散余弦变换 DGPF 德国摄影测量协会, Fernerkundung und Geoinformation(德国摄影测量、遥感和地理信息学会) DGZfP Deutsche Gesellschaft für Zerstörungsfreie Prüfung(德国无损检测学会) DIN Deutsches Institut für Normung(德国标准化研究所) DLT 直接线性变换 DMD 数字镜面装置 DOF 自由度 DRAM 动态随机存取存储器 DSM 数字表面模型DTP 桌面出版 DVD
课程结构和详细的教学大纲 - (R23 ...
开发工程师为实用应用所需的矩阵代数技术。查找本征值和本征媒介并使用线性转换解决问题在更高维度中学习微积分的重要工具。熟悉几个变量的功能,这些函数可用于优化。熟悉两个和三个维度的几个变量功能的双重和三个积分。单位-I:矩阵矩阵的矩阵等级,由echelon形式,正常形式。cauchy –binet公式(无证明)。线性方程式的高斯 - jordan方法系统的非奇异矩阵倒数:通过高斯消除方法的均质和非均匀方程的求解系统,高斯·塞德尔迭代方法。单位-II:线性变换和正交转换:特征值,特征媒介及其特性(无证据证明),基质的对角线化,Cayley-汉密尔顿定理(没有证明),cayley-hamilton Theorem,quadratic of quadrations of quadrations of quadrations of quadration fore the quadrations fore the quadrations的逆和力量的逆和力正交转换单元-III:微积分平均值定理:Rolle的定理,Lagrange的平均值定理,其几何解释,Cauchy的平均值定理,Taylor's和Maclaurin定理以及剩余(无证据),问题和上述定理的剩余(无证据)。单位-IV:部分分化和应用(多变量微积分)
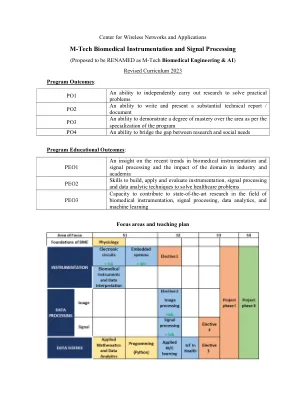
M-Tech 生物医学仪器和信号处理
CO1 能够理解数据挖掘过程中涉及的步骤(例如预处理、分类、回归、聚类和可视化)并将其应用于医疗数据的分析。 CO2 能够描述不同的预测分析方法及其在医疗领域的应用。 CO3 能够评估来自不同来源的数据以创建有意义的演示文稿。 课程内容 使用 Python 进行数据分析:了解数据 - (a)属性、数据的统计描述、数据可视化、相似性 - 不相似性、(b)预处理 - 缺失值、噪声数据、数据缩减、数据转换 - 规范化、标准化、分箱、聚类。 使用 Python 进行应用数学:数学基础 - 线性代数 - 向量、矩阵、特征值、特征向量、奇异值分解、降维、主成分分析、线性变换。概率与统计:随机变量、概率分布、分布函数和属性、离散和连续、统计推断 - 估计和假设检验。机器学习(第 1 部分):机器学习基础、线性回归和逻辑回归(分类)。(第 2 部分将在下学期的应用机器学习课程中继续)教材 1. Jiawei Han 和 Micheline Kamber 编写的《数据挖掘概念和技术》 2. Rohatgi 和 Saleh 编写的《概率与统计简介》。 3. Christian Albright 和 Wayne Winston 编写的商业分析:数据分析与决策
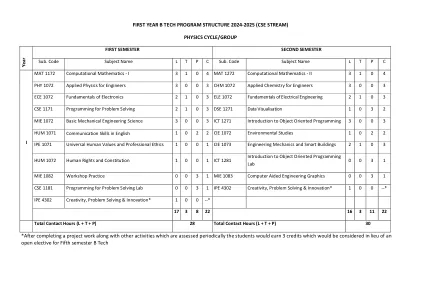
第一年 B TECH 课程结构 2024- ...
用数值方法求解方程。• CO5:应用插值概念求解数值微分和积分问题。教学大纲:矩阵代数:基本列变换和行变换、通过基本行运算求逆矩阵、矩阵的梯形和秩、线性方程组:一致性、高斯消元法、高斯-乔丹法、雅可比法和高斯-赛德尔法求解、特征值和特征向量:基本性质、谱矩阵分解、对角化、矩阵的幂。向量空间:向量概念向高维的推广、广义向量运算、向量空间和子空间、线性独立性和跨度、基。内积空间和 Gram-Schmidt 正交化过程。线性变换。微分方程及应用:一阶和高阶线性微分方程。用逆微分算子、参数变分法和待定系数法求解齐次和非齐次线性方程。代数和超越方程的解:参数曲线的追踪:摆线和相关曲线。二分法、试位法、牛顿-拉夫森法。用牛顿-拉夫森法求解非线性方程组。插值:有限差分和除差分。牛顿-格雷戈里和拉格朗日插值公式。牛顿除差插值公式。离散数值微分、数值积分:梯形法则、辛普森 1/3 法则和辛普森 3/8 法则。常微分方程的数值解:泰勒级数法、修正欧拉法、龙格-库塔法。参考书:
使用空间不连贯的衍射网络
摘要。作为光学处理器,一种衍射深神经网络(D 2 NN)利用通过机器学习设计的工程衍射表面来执行全光信息处理,并以薄光学层以光的速度完成其任务。具有足够的自由度,D 2 NN可以使用空间相干的光执行任意复合物值线性变换。同样,D 2 NN还可以使用空间不连贯的照明执行任意线性强度转换。但是,在空间不连贯的光线下,这些转换是非负的,在视图的输入场上作用于衍射限量的光学强度模式。在这里,我们将空间不连贯的d 2 NN的使用扩展到复杂值的信息处理,用于使用空间不相互分的光执行任意复合物值线性转换。通过模拟,我们表明,随着优化的衍射特征的数量增加超出了由输入和输出空间带宽产品乘法所决定的阈值,因此在空间上不相互不相互的衍射视觉处理器可以近似于使用Incoherent Incoherent Illumentiner的所有复杂的复杂价值线性转换,并用于全部流动图像仿真。这些发现对于使用各种形式的基于表面的光学处理器的自然光的信息在自然光下的全光处理很重要。
双向探出,用于MR图像的脑肿瘤分割
摘要:近年来,基于深度学习的网络在MR图像的脑肿瘤分割方面取得了良好的性能。在现有网络中,U-NET已成功应用。在本文中,它提出了深度学习的双向卷积LSTM XNET(BCONVLSTMXNET),用于分割脑肿瘤并使用GoogleNet分类肿瘤和非肿瘤。对BRATS-2019数据集进行了评估,并获得了肿瘤和非肿瘤分类的结果:0.91,精度:0.95:0.95,召回:1.00&F1得分:0.92。类似地,对于获得精度的脑肿瘤的分割类似:0.99,特定山脉:0.98,灵敏度:0.91,精度:0.91&F1得分:0.88。关键字:convlstm; Googlenet;线性变换(LT); Notch过滤器; X-NET 1简介大脑控制并协调许多重要的身体功能。正常细胞会产生,生长和死亡,当人体不需要它们时,异常细胞被称为癌症。当异常细胞在大脑的任何部分内部产生时,就会发生脑肿瘤。有两种主要类型的肿瘤,即恶性肿瘤和良性肿瘤。良性脑肿瘤是非癌性的,恶性肿瘤是癌性的。转移性脑肿瘤发生时,当位于人体另一个器官的癌症传播到大脑时,所有癌症中有40%扩散到大脑和中枢神经系统,最多一半的转移性脑肿瘤来自肺癌。在10,000个人群中,有5至10人影响印度的中枢神经系统(CNS)肿瘤[1]。
课程与教学大纲
CO1:应用矩阵理论和向量微积分的概念。 CO2:开发求解微分方程的分析方法。 CO3:应用有限差分和有限体积法求解微分方程。 CO4:在工程问题中实施分析和计算技术。矩阵线性方程组的数学运算、一致性 - 向量空间、线性相关性和独立性、基础和维度 - 线性变换 - 投影 - 正交矩阵、正定矩阵、特征值和特征向量、矩阵的相似性、对角化、奇异值分解。矢量场、线积分、曲面积分 - 变量变换、格林定理、斯托克斯定理和散度定理。常微分方程 (ODE)、初值问题及其求解技术、二阶常微分方程的通解、齐次和非齐次情况、边界值问题、Sturm-Liouville 问题和 ODE 系统 - 偏微分方程 (PDE)、柯西问题、特征法、二阶 PDE 和分类、边界条件类型、热、波和拉普拉斯方程的公式和解。使用 MATLAB/python 进行 ODE 和 PDE 的数值实现 - ODE:初值问题:一阶和高阶方法、边界值问题、射击方法、数据拟合、最小二乘 - 标量传输方程的一阶和高阶数值方法、热、波和拉普拉斯方程的有限差分方法。与该计划相关的案例研究:地震波的声学模型、非均匀介质中的扩散、两个平板之间的流动发展、焊接问题、固体材料中的热传导、扩散的相场解(Allen Cahn 1D 解)、两个或多个分子与 Lennard-Jones 势相互作用的解等。
电子与电信技术硕士
MTEC101 工程师高等数学 单元 1 傅里叶变换 - 简介、傅里叶积分定理、傅里叶正弦和余弦积分、傅里叶积分的复数形式、傅里叶变换、逆傅里叶变换、性质、调制定理、傅里叶变换的卷积定理、帕塞瓦尔恒等式、函数导数的傅里叶变换、傅里叶与拉普拉斯变换之间的关系。 单元 2 Z 变换 - 简介、Z 变换的性质、逆 Z 变换的求值。 单元 3 矩阵和线性方程组 - 通过高斯消元法及其改进法解线性联立方程、Crout 三角化方法、迭代方法 - 雅可宾方法、高斯-赛达尔方法、通过迭代确定特征值。单元 4 保角映射-保角映射、线性变换、双线性变换、施瓦茨-克里斯托费尔变换。单元 5 变分法-欧拉-拉格朗日微分方程、最速降线问题及其他应用。等周问题、汉密尔顿原理和拉格朗日方程。瑞利-里兹法、伽辽金法。参考文献:1. 高等工程数学 - 作者:BS Grewal 博士;Khanna Publishers 2. 傅里叶级数与边界值问题 - 作者:Churchill;McGraw Hill。3. 复变量与应用 - 作者:Churchill;McGraw Hill。4. 变分法 - 作者:Elsgole;Addison Wesley。5. 变分法 - 作者:Galfand & Fomin;Prentice Hall。 6. 积分变换的使用 - 作者:IN Sneddon、Tata McGraw Hill。