XiaoMi-AI文件搜索系统
World File Search System线性响应
通过高谐波一代中的Quasiperiodic Aubry-André-Harper链中的多纹理和移动性边缘
我们表明，高谐波光谱学为探测线性响应范围以外的准晶体的电子特性提供了高级途径。着眼于Aubry-André-Harper（AAH）链，我们从谐波发射强度中提取了多重型光谱，这是电子态在准晶体中电子状态空间分布的重要指标。此外，我们解决了迁移率边缘的检测，划定广义AAH模型中局部和扩展的特征状态的重要能量阈值。这些迁移率边缘的精确识别阐明了金属 - 绝缘体的跃迁以及这些边界附近的电子状态的行为。将高谐波光谱与AAH模型合并，为理解排序晶体中的本地化与扩展状态之间的相互作用提供了一个有力的框架，以在线性响应研究中未捕获的极宽的能量范围，从而为指导未来的实验研究提供了宝贵的见解。
AN000394 - 使用气相色谱 - 质谱法的锂离子电池电解质组件的分析
结果和讨论在溶解能力方面进行了比较，包括乙酸乙酯，丙酮，己烷，甲苯，乙醇和三氯甲烷的不同稀释溶剂。只有用乙酸乙酯才能接受靶酯化合物的溶解作用，该乙酸乙酯被选为本研究的稀释溶剂。五个水平的浓度（4、10、20、50和100 mg/L），用于验证线性响应，检测极限（LOD），定量极限（LOQ）和面积计数可重复性（RSD％）。图1.
3。量子统计物理
3量子相变1 3.1量子 - 经典连接。。。。。。。。。。。。。。。。。。。。。。1 3.1.1经典的量子。。。。。。。。。。。。。。。。。。。。。。。。。。1 3.1.2量子到古典。。。。。。。。。。。。。。。。。。。。。。。。。。10 3.2路径积分。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。16 3.2.1 Langevin方程的Wiener Construction。。。。。。。。。16 3.2.2 Feynman Path积分结构。。。。。。。。。。。。。。。18 3.2.3 Wick的旋转。。。。。。。。。。。。。。。。。。。。。。。。。。。。。20 3.2.4基态。。。。。。。。。。。。。。。。。。。。。。。。。。。。22 3.2.5经典限制。。。。。。。。。。。。。。。。。。。。。。。。。。。。。23 3.2.6量子校正。。。。。。。。。。。。。。。。。。。。。。。。。。23 3.2.7谐波振荡器。。。。。。。。。。。。。。。。。。。。。。。。23 3.2.8隧道和激体。。。。。。。。。。。。。。。。。。。。。。。。25 3.2.9还原系统。。。。。。。。。。。。。。。。。。。。。。。。。。。30 3.3相关性能。。。。。。。。。。。。。。。。。。。。。。。。。。。。33 3.3.1期望值和相关性。。。。。。。。。。。。。。。。。。33 3.3.2线性响应和kubo公式。。。。。。。。。。。。。。。。。。。35 3.3.3线性响应和onsager关系。。。。。。。。。。。。。。。。。37 3.3.4因果关系和Kramers-Kronig。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 38 3.3.5 KMS关系。 。 。 。 。 。 。 。 。 。 。37 3.3.4因果关系和Kramers-Kronig。。。。。。。。。。。。。。。。。。。。。。38 3.3.5 KMS关系。。。。。。。。。。。。。。。。。。。。。。。。。。。39 3.3.6流动性散文定理。。。。。。。。。。。。。。。。。。40 3.4量子相变。。。。。。。。。。。。。。。。。。。。。。。。。。。42 3.4.1量子链链。。。。。。。。。。。。。。。。。。。。。。。。44 3.4.2二元性。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。48 3.4.3 Jordan-Wigner转换。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 48 3.4.4 Bogoliubov变换。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 50 3.附录。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 53 3.A.1自旋1/2。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 。 53 3.A.2 Pauli矩阵。48 3.4.3 Jordan-Wigner转换。。。。。。。。。。。。。。。。。。48 3.4.4 Bogoliubov变换。。。。。。。。。。。。。。。。。。。。50 3.附录。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。53 3.A.1自旋1/2。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。53 3.A.2 Pauli矩阵。53 3.A.2 Pauli矩阵。。。。。。。。。。。。。。。。。。。。。。。。。。。54 3.A.3矩阵元素。。。。。。。。。。。。。。。。。。。。。。。。。。。55 3.A.4固定相近似。。。。。。。。。。。。。。。。。。。。57
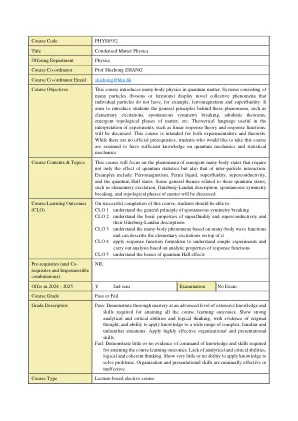
课程代码Phys8552标题缩合物...
课程目标本课程介绍了量子物质中的多体物理学。由许多颗粒（玻色子或费米子）组成的系统显示出新型的集体现象，例如，单个颗粒没有类似铁磁性和超流量。它旨在介绍这些现象背后的一般原则，例如基本激发，自发对称性破坏，绝热定理，物质的新兴拓扑阶段等。将讨论用于解释实验的解释（例如线性响应理论和响应函数）的理论语言。本课程均针对实验者和理论家。尽管没有官方先决条件，但想参加本课程的学生被认为对量子力学和统计力学有足够的知识。
分配器印刷铋基磁场传感器，具有非饱和大磁阻，适用于非接触式交互表面
印刷电子是一个充满活力的研究和技术领域，可获得按需功能元件。[1–3] 近年来，已报道了具有半导体、[4] 光电、[5] 储能[6] 和磁性 [7] 特性的印刷电子。特别是印刷磁阻传感器已证明其作为非接触式电磁开关 [8,9] 和非接触式交互式皮肤平台的相关性。[10] 这些磁敏感复合材料是通过将铁磁磁阻 (MR) 颗粒或薄片分散在各种凝胶状或热塑性粘合剂溶液中而制成的（表 1）。[9–17] 虽然这些贡献在过去十年中显著推动了该领域的发展，但由于组成颗粒或薄片的复杂性和高生产成本，这些技术的大规模应用仍未实现。表现出高达 37% 的巨磁电阻效应 (GMR) 的薄片由多层异质结构组成，需要逐层沉积亚纳米厚的薄膜。[9–13] 需要精确调整层的厚度以实现可测量的磁阻变化。这导致表现出 GMR 的粉末的生产成本增加。为了解决 GMR 粉末的可扩展性问题，采用了表现出各向异性磁阻 (AMR) 的商品可用铁磁材料颗粒。[14] 然而，测得的 AMR 效应降低到 0.34%。此外，这些 MR 技术通常在 500 mT 以下的磁场下具有线性响应，并且在此之外几乎不敏感。缺乏一种具有强磁阻信号并在宽磁场范围内工作的可打印商品级材料。使用打印技术瞄准更广泛的磁场可以实现新型低成本技术解决方案，从非接触式开关应用到机械的工业监控。采用传统的印刷方法实现大规模生产和高磁场下的线性响应需要新材料的开发。
使用稳定同位素标记标准和三重四极杆质谱法实施针对性和标准化临床代谢组学的指南
2. QC 样品 — 通常是该批次研究样品的混合样品，理想情况下结合同位素标记的代谢物混合物（例如 CIL 的 QReSS 混合物 25 ），每 8-10 个研究样品后运行一次。使用混合 QC 样品的主要优势在于，它能够评估所研究的每种代谢物的保留时间和信号稳定性（图 6）。对于大批次，在运行过程中观察到一些信号丢失并不罕见，QC 样品数据可用于有效地应用信号校正算法。还建议在运行开始时运行 QC 样品稀释系列，例如未稀释、2 倍稀释、4 倍稀释和 8 倍稀释。这有助于确认所研究代谢物的线性响应。
一种用于快速和多路复用等离子体检测高分子量和低分子量分析物的全集成微型光学生物传感器
基于等离子体传感方案的光学生物传感器将高灵敏度和选择性与无标记检测相结合。然而，使用笨重的光学元件仍然阻碍了获得在实际环境中进行分析所需的微型系统的可能性。这里展示了一种基于等离子体检测的完全微型光学生物传感器原型，它能够快速和多路复用地感测高分子量和低分子量（80 000 和 582 Da）的分析物作为牛奶的质量和安全参数：一种蛋白质（乳铁蛋白）和一种抗生素（链霉素）。光学传感器基于以下智能集成：i）用作发光和光感应元件的微型有机光电器件和 ii）用于高灵敏度和特异性局部表面等离子体共振 (SPR) 检测的功能化纳米结构等离子体光栅。该传感器提供定量和线性响应，达到 10 − 4 的检测限
时间相关密度泛函理论的最小辅助基组及其与紧束缚近似的比较：应用于银纳米
通过第一性原理方法对等离子体纳米粒子的光谱进行建模需要耗费大量的计算资源，因此需要具有高准确度/计算成本比的方法。本文，我们表明，如果在辅助基组中每个原子仅采用一个 s 型函数，并采用适当优化的指数，则可以大大简化时间相关密度泛函理论 (TDDFT) 方法。这种方法（称为 TDDFT-as，代表辅助 s 型）可以预测不同尺寸和形状的银纳米粒子的激发能量，与参考 TDDFT 计算相比，平均误差仅为 12 meV。TDDFT-as 方法类似于线性响应处理的紧束缚近似方案，但适用于原子跃迁电荷，这里精确计算（即没有来自群体分析的近似）。我们发现，原子跃迁电荷的精确计算大大改善了宽能量范围内的吸收光谱。
![arXiv:2406.18662v1 [quant-ph] 2024 年 6 月 26 日](/simg/g:\will\search\icon\source\b\bb2fa075e350d32e7110994b026449abf44f3c4a.png)
arXiv:2406.18662v1 [quant-ph] 2024 年 6 月 26 日
用于计量的量子系统可以提供比传统系统更高的精度。可以通过最大化量子 Fisher 信息 (QFI) 来优化量子传感器的设计，该信息表征了理想测量的参数估计精度。在这里，我们将量子系统的响应视为一种估计已缓慢开启的外部扰动强度的方法。推导出 QFI 的一般表达式，该表达式也适用于有限温度下热力学极限下的相互作用多体系统，并且可以与线性响应传输系数相关联。对于量子点纳米电子器件，我们表明电子相互作用可以导致 QFI 随系统尺寸呈指数级缩放，强调量子资源可以在整个 Fock 空间中得到利用。电压和场的精确估计也可以通过实际的全局测量（例如电流）来实现，这使得量子电路成为计量应用的良好候选者。
全息超流体的关键和近乎关键的放松
我们研究了淬灭后全息超流体的放松，当末端状态被调谐到临界点，或者非常接近它时。通过以数值方式求解运动的整体方程，我们证明了在前一种情况下，系统表现出功率定律的损失以及紧急的离散量表不变性。后一种情况是由临界放慢速度主导的政权，我们表明在延迟期限下降开始之前存在一个中间时间范围，该系统的行为与其功率定律下降的临界点相似。我们进一步假设一个现象学的毛pitaevskii样方程（对应于Hohenberg和Halperin的模型F），该方程能够对近临界淬灭到超级流体和正常阶段后的全息超氟中全息超流体的行为进行定量预测。有趣的是，描述非线性时间演化的现象学方程的所有参数，可以用静态平衡溶液和线性响应理论的信息固定。