XiaoMi-AI文件搜索系统
World File Search System确保地月空间和地球外海第一岛的安全
二体问题和三体问题:对于在地心轨道上绕地球运行的卫星,影响其路径的力是众所周知的。在二体问题中,主要因素是两个天体(在本例中为地球和卫星)的质量以及它们之间的距离。在这种轨道下,有控制卫星运动的解方程。然而,在地月轨道下,月球的额外引力使运动方程变得非常复杂。在三体问题中,主要因素是三个天体(现在是地球、卫星和月球)的质量以及地球与月球、地球与卫星、月球与卫星之间的距离。三体问题中物体的轨迹没有通用解。在地月轨道下,有几个特殊位置,地球和月球的引力平衡并达到平衡。这些位置称为拉格朗日点。
物理循环-CSE-stream-2022-scheme.pdf
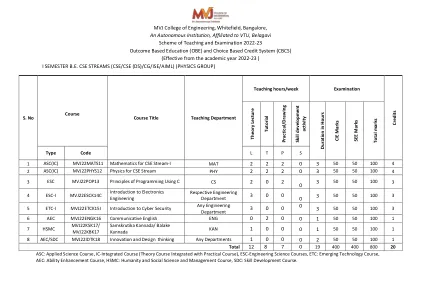
•熟悉与一个变量相关的微积分的重要性,并且在计算机科学和工程方面可进行多变量。•通过应用普通微分方程来分析计算机科学和工程问题。•将模块化算术知识应用于计算机算法。•发展线性代数的知识以求解方程系统。模块1 L1,L2和L3 8小时与计算机科学和工程有关的极性坐标和曲率简介。极坐标,极曲线,半径矢量与切线之间的角度以及两条曲线之间的角度。踏板方程。曲率和曲率半径 - 笛卡尔,参数,极性和踏板形式。问题。自学:曲率的中心和圆圈,进化和灭绝。应用:结构设计和路径,材料强度,弹性。模块-2 L1,L2和L3 8小时串联扩展和部分分化的介绍计算机科学领域和
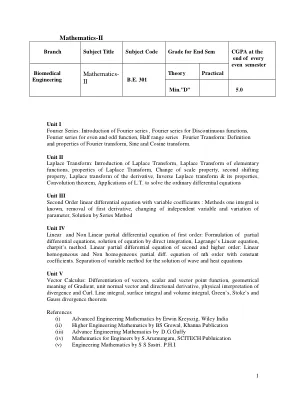
数学-II - 分支学科名称学科代码年级...
第一单元 傅里叶级数:傅里叶级数简介、不连续函数的傅里叶级数、偶函数和奇函数的傅里叶级数、半程级数 傅里叶变换:傅里叶变换的定义和性质、正弦和余弦变换。 第二单元 拉普拉斯变换:拉普拉斯变换简介、初等函数的拉普拉斯变换、拉普拉斯变换的性质、尺度变化性质、二阶平移性质、导数的拉普拉斯变换、逆拉普拉斯变换及其性质、卷积定理、应用 LT 解常微分方程 第三单元 变系数二阶线性微分方程:方法 已知一个积分、去除一阶导数、改变独立变量和改变参数、用级数法求解 第四单元 一阶线性和非线性偏微分方程:偏微分方程的公式、直接积分解方程、拉格朗日线性方程、查皮特方法。 二阶及高阶线性偏微分方程:具有常系数的 n 阶线性齐次和非齐次偏微分方程。分离变量法解波动和热方程 第五单元 向量微积分:向量的微分、标量和向量点函数、梯度的几何意义、单位法向量和方向导数、散度和旋度的物理解释。线积分、面积积分和体积积分、格林散度定理、斯托克斯散度定理和高斯散度定理 参考文献