XiaoMi-AI文件搜索系统
World File Search SystemINAS - AL混合设备中的干涉测量学单拍测量
非阿布莱安人的融合是仅测量拓扑量子计算中的基本操作1。在一维拓扑超导体(1DTSS)2–4中,融合量相当于确定Majorana零模式(MZMS)的共享费米亚奇偶校验。在这里,我们介绍了与Fusion规则未来测试兼容的设备体系结构5。我们在砷氧化胺 - 铝 - 铝异源结构中实施了单次干涉测量,并具有栅极定义的超导纳米线12-14。干涉仪是通过将邻近的纳米线与量子点耦合形成的。纳米线导致这些量子点的量子电容的状态依赖性转移高达1 ff。我们的量子电气测量值显示了通量H /2 e - 周期性双峰性,其信噪比(SNR)在最佳通量值下为1.6μm。从量子电气压测量的时间迹线开始,我们在两个相关状态中提取了一个相关状态的停留时间,在大约2 t的平面磁场时长度超过1 ms。我们讨论了根据拓扑上的微不足道和非本质起源的测量的解释。较大的电容偏移和较长的中毒时间可实现奇偶校验测量,分配误差概率为1%。
具有恒定误差
在过去的一年中,在量子误差更正领域发生了许多发展。最近显示了如何执行可容忍的量子计算,而〜,〜,每值或每个门的一个时间步长或每扇门的断层的概率是小毛的。本文缩小了差距,并显示了如何执行误差概率q小于某个恒定阈值的误差时执行容错量子计算。成本在时间和空间上是多层次的,在量子计算过程中未使用测量值。对于仅在最近的邻居上工作的量子cirs也显示了相同的结果。为了达到这种噪声阻力,我们使用串联的量子误差校正代码。提出的方案是一般的,并且可以使用任何量子代码,这些量子代码是某些RESTM”,即它是“适当的量子代码”。恒定阈值R10是指定正确代码的参数的函数。我们提出了两个明确的量子代码类别。头等舱将经典的秘密与多项式共享。代码是在带有P元素的字段上定义的,这意味着Elementary量子粒子不是量子,而是“ Qupit”。第二类使用已知类别的量子代码,并将其转换为适当的代码。我们估计阈值qo为= 10-6。希望 - 本文完全激励搜索具有较高阈值的适当量子代码,此时量子计算变得可行。
电力电子与电力系统课程大纲
1. 计算技能:基本编程结构:数据类型、数组、指针、链接列表和树、语句、I/O、条件、循环、函数、类/对象。 2. 通信技术:通信标准、2G/3G/4G/5G、ZigBee、BLE、Wi-Fi、LTE、IEEE 802.11x、数据速率、覆盖范围、功率、计算、带宽、传感、处理、通信供电、通信网络、拓扑、层/堆栈架构、QoS。 3. 通信系统:通信系统的物理层描述、量化、数据格式化和成帧、点对点链路的容量、链路预算分析、多址技术、网络路由 4. 数据分析:组合学、有限样本空间上的概率、联合和条件概率、独立性、总概率;贝叶斯规则及应用。 5. 数字通信:通带表示、基带等效 AWGN 信道、数据调制和解调、调制波形的合成、离散数据检测、加性高斯白噪声 (AWGN) 信道、使用匹配滤波器实现信噪比 (SNR) 最大化、AWGN 信道的误差概率、MAP 和 ML 检测、数字调制技术、无线信号传播和信道模型。6. 数字信号处理:采样、连续和离散时间变换、LTI 系统的频域分析、FFT 实现、算法、滤波器设计:IIR 和 FIR 滤波器、采样率转换。
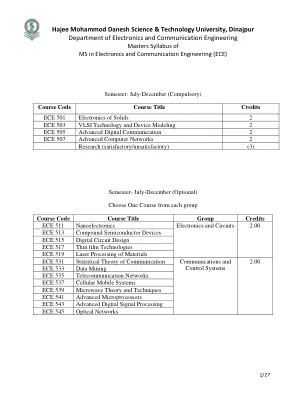
哈吉穆罕默德丹尼什科技大学,迪纳杰布尔
推荐书籍: [1] Wai-Kai Chen,“VLSI 技术(工程原理与应用)”,CRC press,2003,第 1 版,ISBN:978-0849317385。 [2] Kwyro Lee、Michael shur、Tor A. Fjeldly 和 Tron Ytterdal,“VLSI 的半导体器件建模”,Prentice Hall,1997,第 1 版,ISBN:978-0138056568。 ECE 505:高级数字通信 学分:2.00 学习时间:2 小时/周 概率与随机过程回顾。无记忆信道上的功率谱与通信:同步数据脉冲流的 PSD、M 元马尔可夫源、卷积编码调制、连续相位调制、无记忆信道上的标量和矢量通信、检测标准。相干和非相干通信:相干接收器、WGN 中的最佳接收器、IQ 调制和解调、随机相位信道中的非相干接收器、M-FSK 接收器、瑞利和莱斯信道、部分相干接收器 – DPSK、M-PSK、M-DPSK、BER 性能分析。带限信道和数字调制:眼图、存在 ISI 和 AWGN 时的解调、均衡技术、IQ 调制、QPSK、O/4-QPSK、QAM、QBOM、BER 性能分析、连续相位调制、CPFM、CPFSK、MSK、OFDM。块编码数字通信:结构和性能、二进制块码、正交、双正交、超正交-香农信道编码定理、信道容量、匹配滤波器、扩频通信概念、编码 BPSK 和 DPSK 解调器、线性块码、汉明、戈莱、循环、BCH、里德-所罗门码。卷积编码数字通信:使用多项式、状态图、树形图和网格图表示代码,使用最大似然、维特比算法、顺序和阈值方法的解码技术 - BPSK 和维特比算法的误差概率性能。
通过预测分析增强网络安全
摘要 - 启用6G的车辆网络面临着确保超级可靠的低延迟通信(URLLC)及时提供安全关键信息的挑战。车辆对所有(V2X)通信系统的现有资源分配方案主要依赖于基于传统优化的算法。但是,由于解决方案方法的高复杂性和沟通开销,这些方法通常无法保证在动态车辆环境中URLLC应用的严格可靠性和潜伏期需求。本文提出了一种基于联合功率和块长度分配的基于新颖的深钢筋学习(DRL)框架,以最大程度地减少基于URLLC的下链接V2X通信系统的有限块长度(FBL)示例中最坏的解码错误概率。该问题被称为非凸层混合构成非局部编程问题(MINLP)。最初,基于在块长度中得出解码误差概率的关节凸的基础,开发了一种基于优化理论的算法,并在感兴趣的区域内传输功率变量。随后,提出了一种有效的事件触发的基于DRL的算法来解决关节优化问题。将事件触发的学习纳入DRL框架中,可以评估是否启动DRL流程,从而减少DRL过程执行的数量,同时保持合理的可靠性性能。DRL框架由两层结构组成。在第一层中,在中央教练中建立了多个深Q-NETWORKS(DQN)以进行块长度优化。第二层涉及参与者 - 批评网络,并利用了基于深层的确定性策略颁奖典礼(DDPG)的算法来优化功率分配。仿真结果表明,所提出的事件触发的DRL方案可以实现关节优化方案的95%,同时为不同的网络设置减少DRL执行最多24%。
重新布线蛋白质序列和结构生成模型以增强蛋白质稳定性预测
快速增长的数据需要可靠且持久的存储解决方案。DNA由于其高信息密度和长期稳定性而成为一种有希望的媒介。但是,DNA存储是一个复杂的过程,每个阶段都会引入噪声和错误,包括合成错误,存储衰减和测序错误,它需要对错误校正的代码(ECC)才能获得可靠的数据恢复。要设计一种最佳数据恢复方法,对DNA数据存储通道中噪声结构的综合理解至关重要。由于在体外运行DNA数据存储实验仍然很昂贵且耗时,因此必须进行模拟模型,以模仿真实数据中的误差模式并模拟实验。现有的仿真工具通常依赖固定的误差概率或特定于某些技术。在这项研究中,我们提出了一个基于变压器的生成框架,用于模拟DNA数据存储通道中的错误。我们的模拟器将寡素(DNA序列写入)作为输入,并生成错误的输出DNA读取,与常见DNA数据存储管道的真实输出非常相似。它捕获了随机和有偏见的误差模式,例如K-MER和过渡错误,无论过程或技术如何。我们通过分析两个使用不同技术处理的数据集来证明模拟器的有效性。在第一种情况下,使用Illumina Miseq处理,由DDS-E-SIM模拟的序列显示出与原始数据集的总误率偏差仅为0.1%。第二次使用牛津纳米孔技术进行的偏差为0.7%。基本级别和K-MER错误与原始数据集紧密对齐。此外,我们的模拟器从35,329个序列中生成100,743个独特的橄榄岩,每个序列读取五次,证明了其同时模拟偏置错误和随机属性的能力。我们的模拟器以优越的精度和处理多种测序技术的能力优于现有的模拟器。
对称多量子系统中纠缠研究中的信息图及其在 Lipkin–Meshkov–Glick D 级原子模型中量子相变的应用
信息图被用来讨论两种不同信息测度之间的关系,如冯·诺依曼熵与误差概率[1],或冯·诺依曼熵与线性熵[2]。对于线性(L)熵和冯·诺依曼(S)熵,通常对任何有效的概率分布ρ绘制(L(ρ),S(ρ))图。这里,ρ也可以表示量子系统的密度矩阵(或者更确切地说是具有其特征值的向量),这也是本文的主要兴趣所在。我们特别关注由此产生的信息图区域的边界,其中相关的概率分布(或密度矩阵)将被表示为“极值”。在参考文献[3]中,对两个量子比特的熵进行了比较(有关离子-激光相互作用的情况,另见[4])。在 [5] 中,对任意熵对的信息图进行了详细研究。文中证明了,对于某些条件(线性、冯·诺依曼和雷尼熵满足),极值密度矩阵始终相同。文中给出了反例,但一般来说,偏差会非常小,并且可以安全地假设这些极值密度矩阵具有普适性。在本文中,我们将使用信息图来获取对称多量子系统中粒子纠缠的全局定性信息,该系统由广义“薛定谔猫”(多组分 DCAT)态(在 [6] 中首次引入,作为振荡器的双组分偶态和奇态)描述。这些 DCAT 态原来是 U(D)自旋相干(准经典)态的 ZD−12 宇称改编,它们具有弱重叠(宏观可区分)相干波包的量子叠加结构,具有有趣的量子特性。为此,我们使用一和二量子Dit 约化密度矩阵 (RDM),它是通过从由 cat 态描述的 N 个相同量子Dit 的复合系统中提取一两个粒子/原子,并追踪剩余系统获得的。众所周知(见 [3] 及其参考文献),这些 RDM 的熵提供了有关系统纠缠的信息。我们将绘制与这些 RDM 相关的信息图,并提取有关一和二量子Dit 纠缠的定性信息,以及相应 RDM 的秩,这也提供了有关原始系统纠缠的信息 [7]。我们将应用这些结果来表征 3 级全同原子 Lipkin–Meshkov–Glick 模型中发生的量子相变 (QPT),以补充 [ 8 ] 的结果。具体来说,我们已经看到,一和二量子 DIT RDM 的秩可以被视为检测 QPT 存在的离散序参量前体。本文结构如下。第 2 节回顾了信息图的概念,描述其主要属性,特别是关于秩的属性。第 3 节回顾了 U(D) 自旋相干态的概念及其 ZD−12 宇称适配版本 DCAT。在第 4 节中,我们计算了 2CAT 和 3CAT 的一和二量子 Dit RDM、它们的线性熵和冯诺依曼熵,绘制了它们并构建了相关的信息图。在第 5 节中,我们使用信息图提供有关 Lipkin–Meshkov–Glick (LMG) 模型中 QPT 的定性信息。第 6 节致力于结论。