XiaoMi-AI文件搜索系统
World File Search System选修课程提供2025-26.docx
FOREIGN LANGUAGE PHYSICAL EDUCATION CAREER AND TECHNICAL EDUCATION CAREER AND TECHNICAL EDUCATION ___SPANISH I ___SPANISH I HONORS ___SPANISH II ___SPANISH II HONORS ___SPANISH III ___SPANISH FOR NATIVE SPEAKERS I ___SPANISH FOR NATIVE SPEAKERS II ___AP SPANISH ___FRENCH I ___FRENCH II ___FRENCH III ESOL ELECTIVES ___ORAL COMMUNICATION ___COMMUNICATION SKILLS I/II ___READING & LISTENING Band ___ADVANCED BAND I/II/III/IV ___MASTERY BAND I/II/III/IV Chorus ___ ADVANCED CHORUS I/II/III/IV ___MASTERY MIXED CHORUS I/II/III/IV Dance ___MODERN DANCE I/II/III/IV ___DANCE I/II/III/IV ___JAZZ DANCE I/II/III/IV Theatre ___THEATRE ARTS FUNDAMENTALS ___ADVANCED DRAMA I/II/III/IV ___TECHNICAL THEATER I/II/III/IV ___MUSICAL THEATRE I Art ___VISUAL ART I/II ___CERAMICS & POTTERY I/II/III ___DRAWING & PAINTING I/II/III ___摄影I/II ___珠宝/金属工艺I
2025-2026课程目录
途径5:基于证据的途径成功完成了与每个Keystone考试相关的本地建立的基于年级的要求,从而从以下标准中获得了熟练程度和三个工件:从以下标准中至少有一个文物:在任何AP考试中获得3个或更高的AP考试。在任何学科领域成功完成了大学级课程。获得行业认可的证书。接受不是4年计划的大学级课程(例如,贸易学校或社区学院)。从以下内容中不超过两个工件:在任何Keystone考试中得分1500。成功完成服务学习项目(学校批准和至少10个小时)。保证全职工作或军事入伍的信。完成实习,实习或合作ED计划。遵守NCAA D II学术要求。
首尔技术奖学金招聘硕士课程
那些希望申请上述学位课程的人,您应该将申请直接发送到外交事务部,外国就业和旅游部的以下地址,并在2025年3月15日或之前签署了教育部,高等教育和职业教育部高等教育部,高等教育和职业教育部的副本。
BTECH课程的太空科学课程和...
1。学生可以在IIT Indore教师的监督下在研究所外或研究所内部进行BTECH项目。2。暑期实习(如果有的话)将成为B技术项目的一部分。3。选择将在4月30日之前最新。4。持续时间:5月2日至11月5日上周的6-7个月。论文提交的最后日期:12月6日。提交等级的最后日期:12月的第二周
LANC2058 课程大纲.docx
VII. 学生责任 学生有责任了解并遵守与参加本课程相关的所有大学学术规定。这些规定具体包括出勤要求和学生学术行为准则。 学术诚信 大学希望学生以最高的学术诚信对待学术活动。请参阅本科生学术规定。 添加和删除 希望删除或添加课程的学生应查看本科生学术规定。 出勤 苏丹卡布斯大学对学生出勤有明确的要求,详见本科生学术规定。 评估和评分
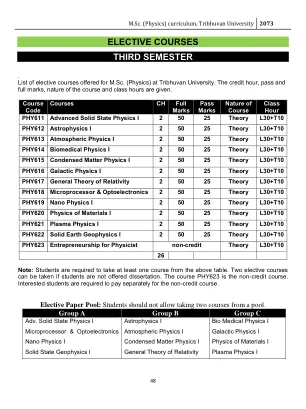
选修课程 - TU 登录门户 - 特里布万大学
物理学。课程内容:1. 简介:[2 小时] 1.1 非相互作用电子气。2. Born-Oppenhemier 近似:[3 小时] 2.1 基本哈密顿量,2.2 绝热近似,2.3 简化电子问题。3. 二次量子化:[5 小时] 3.1 玻色子,3.2 费米子,3.3 费米子算符。4. Hartree-Fock 近似:[4 小时] 4.1 非相互作用极限,4.2 Hartree-Fock 近似,4.3 图表。5. 相互作用电子气:[4 小时] 5.1 均匀电子气,5.2 Hartree-Fock 激发谱,5.3 金属的结合能。 6. 金属中的局部磁矩:[4 小时] 6.1 局部矩:现象学,6.2 平均场解。 7. 局部矩的猝灭:[8 小时] 7.1 近藤问题,7.2 近藤汉密尔顿量,7.3 为什么 J 为负? 7.4 散射和电阻率最小值,7.5 电子-杂质散射振幅,7.6 近藤温度。
2024-2025 高中课程名称和说明
与课程选择和开发、实施和评估相关的教学决策由当地学校法人决定。印第安纳州的学校可能会探索、开发和实施超出这些描述的活动和计划,努力让学生为不断变化的世界做好准备。印第安纳州教育委员会 (SBOE) 规则和公共法 221 要求的学校改进计划为获得精心策划的非标准计划和课程的批准提供了途径。如果课程或计划未在本文件中列出,学校法人可以申请非标准课程豁免。查看印第安纳州教育委员会课程名称和说明网页上“非标准课程豁免”下列出的资源。有关每门课程的教师执照的信息可在此处找到。
凝聚力课程:扫盲更新2023-24
从我们社区的学校进步计划开始,教学团队开会以开发智能目标,以确保所有种族,背景和能力的学生都在高水平上取得成就,证明了三年级的阅读能力和八年级的数学熟练程度,并为成功的大学和职业而毕业。地区的目标是集中于阅读,数学和院长成功的(2023-2026地区目标)。在夏季学院(2023年6月)期间,建立领导团队(BLT)开会,以发展和/或完善其建筑目标,以专注于与学校相关且重要的问题,而BLT认为会影响整个地区目标。建立目标逐渐滴入,以告知和影响PLC的成绩和内容领域团队以及个人教师目标。
印第安纳高中定量推理课程
●4801计算机科学I●4838机械制图和设计II●5236计算机科学II●5249计算机科学III:软件开发帽岩石●5250计算机科学III:数据库●5251计算机科学III:信息学III:信息学:信息学●5253 Computer Science III:Cybersecurity II:Cybersecurity II:Cybersecurity II●56 ARTACTECTART●5652 ARTACTECTER●5652 ARTACTECTERCTINTER●5652 ARTACTECTERT●5652 ARTACTECTERCTINTER●5652 ARTACTECTITIC电子和计算机技术II●7197 BIM体系结构●7200电力和电动机的基础●7202制造原理和设计●7223机械设计Capstone●7351计算机科学中的主题●7352 7361计算机科学●7361电子基础●7362电子基础●7362电子技术●7362电子capstone