XiaoMi-AI文件搜索系统
World File Search System辛普森
名人堂迎来 2 名入选者 - 陆军驻军
5 月 9 日，在刘易斯和克拉克中心举行的仪式上，两个新的影盒揭幕，上面刻有最新入选莱文沃思堡名人堂的人物。1925 年毕业于指挥和参谋学院的退役将军威廉·H·辛普森和前 CGSC 指挥官退役中将约翰·E·米勒是入选名人堂的最新成员。名人堂成立于 1969 年，旨在表彰曾在莱文沃思堡服役并为该设施和美国武装部队的声誉、传统和历史做出重大贡献的军事和民事领导人。联合兵种中心和莱文沃思堡指挥官兼 CGSC 指挥官米尔福德·H·比格尔中将解释说，入选莱文沃思堡名人堂将永久提醒入选者对该地区和军队的领导能力和奉献精神。他说：“当你思考我们今天为什么会在这里时，我相信我们找不到比他们更伟大的美国人、士兵和领导者了，他们塑造了我们的军队，他们塑造了我们目前用来教育未来领导者的方法。”贝格尔强调了辛普森的“极端”奉献精神和智慧如何对今天的军队产生了显著的影响。尽管从未高中毕业，
cal_state_la_parking_brochure_...
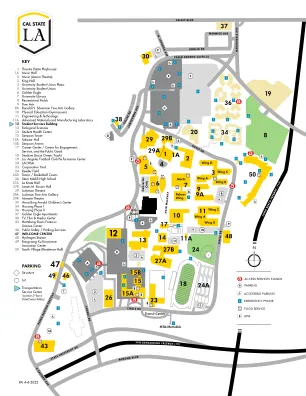
剧院（州立剧院） 音乐厅 音乐（竞技场剧院） 国王厅 大学学生会广场 大学学生会 金鹰大学图书馆 休闲场所 美术 罗纳德·H·西尔弗曼美术馆 体育（体育馆） 工程与技术 先进材料与制造实验室 学生服务大楼 生物科学学生健康中心 辛普森塔 萨拉萨尔厅 辛普森附楼 职业中心 / 参与、服务和公共利益中心 体育场（杰西·欧文斯田径场） 洛杉矶足球俱乐部表演中心 LACHSA 公司庭院 里德球场 网球场 / 篮球场 斯特恩马萨诸塞州高中 拉克雷茨厅 詹姆斯·M·罗瑟厅 勒克曼剧院 勒克曼美术馆 私密剧院 安娜·宾阿诺德儿童中心 一期住房 二期住房 金鹰公寓 电视、电影和媒体中心 赫兹伯格-戴维斯法医科学中心 公共安全 / 停车服务 欢迎中心 加氢站 徐荣祥生物科学创新中心住宅区
校园地图 4-4-2022 p
剧院（州立剧院） 音乐厅 音乐（竞技场剧院） 国王厅 大学学生会广场 大学学生会 金鹰大学图书馆 休闲场所 美术 罗纳德·H·西尔弗曼美术馆 体育（体育馆） 工程与技术 先进材料与制造实验室 学生服务大楼 生物科学 学生健康中心 辛普森塔 萨拉萨尔厅 辛普森附楼 职业中心/参与、服务和公共利益中心 体育场（杰西·欧文斯田径场） 洛杉矶足球俱乐部表演中心 LACHSA 公司庭院 里德球场 网球场/篮球场 斯特恩马萨诸塞州高中 拉克雷茨厅 詹姆斯·M·罗瑟厅 勒克曼剧院 勒克曼美术馆 私密剧院 安娜·宾 阿诺德儿童中心 一期住房 二期住房 金鹰公寓 电视、电影和媒体中心 赫兹伯格-戴维斯法医科学中心 公共安全/停车服务 欢迎中心 加氢站 徐荣祥生物科学创新中心 南村（宿舍楼）
研究兴趣小组（钻机）议程•来自...
Agenda • From development biology to regenerative medicine – Francesca Spagnoli & Mauro Giacca • RNA Biology – Chad Swanson & Sasi Conte • Spatial Biology Network –Anita Grigoriadis & Ciro Chiappini • Innovation for Safe and Sustainable Food, nutrition and Health – Paul Sharp & Christer Hogstrand • Inequalities: Local, National & Global - 统计和计算遗传学和基因组学 - 迈克尔·辛普森（Michael Simpson）和凯林（Kerrin Small）•脂质和膜 - Riki Eggert和Jez Carlton
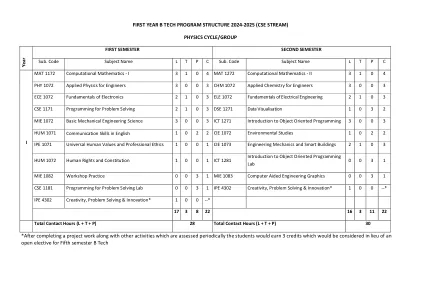
第一年 B TECH 课程结构 2024- ...
用数值方法求解方程。• CO5：应用插值概念求解数值微分和积分问题。教学大纲：矩阵代数：基本列变换和行变换、通过基本行运算求逆矩阵、矩阵的梯形和秩、线性方程组：一致性、高斯消元法、高斯-乔丹法、雅可比法和高斯-赛德尔法求解、特征值和特征向量：基本性质、谱矩阵分解、对角化、矩阵的幂。向量空间：向量概念向高维的推广、广义向量运算、向量空间和子空间、线性独立性和跨度、基。内积空间和 Gram-Schmidt 正交化过程。线性变换。微分方程及应用：一阶和高阶线性微分方程。用逆微分算子、参数变分法和待定系数法求解齐次和非齐次线性方程。代数和超越方程的解：参数曲线的追踪：摆线和相关曲线。二分法、试位法、牛顿-拉夫森法。用牛顿-拉夫森法求解非线性方程组。插值：有限差分和除差分。牛顿-格雷戈里和拉格朗日插值公式。牛顿除差插值公式。离散数值微分、数值积分：梯形法则、辛普森 1/3 法则和辛普森 3/8 法则。常微分方程的数值解：泰勒级数法、修正欧拉法、龙格-库塔法。参考书：
B. e人工智能和机器学习
in science and engineeri Module 1: Laplace Tran Laplace Transforms: Def of Laplace Transform–Lin function, Dirac Delta functio Inverse Laplace Transfo to find the inverse Laplac Transforms Module 2: Fourier Series Introduction to Infinite ser condition, Fourier series of Practical Harmonic Analysis Module 3: Fourier Tran Fourier Transforms: De Transforms, Inverse Fourier Solution of first and second Module 4:数值m有限差，牛顿'lagrange的和逆滞后模块5：多项式方法的数值m解决方案，数值差异集成：辛普森（1/3
印第安纳州，爱荷华城市经理 - Govhr职业中心 COLES - 总裁兼首席执行官 - Govhr职业中心 佛罗里达州迈阿密海滩市 - 经济发展总监
印第安纳州的中心是广场，这是一个历史悠久的城镇广场（最近被称为爱荷华州主要街道社区），它提供了餐馆，商店和企业的融合，全年都充满了各种活动和节日。该市主持了得梅因大都会歌剧院，该歌剧在辛普森校园的Blank表演艺术中心演出。每年夏天，歌剧将200名艺术家带到社区。Indianola还举办了国家气球经典赛 - 每年夏天为期9天的活动，有100多个热气球，这是该国最大的活动之一，是国家气球博物馆的所在地。作为沃伦县席位，沃伦县博览会每年夏天在印第安纳州举行，这是一个超过150年的目的地。
2025年的能源和水发育拨款...
哈罗德·罗杰斯（Harold Rogers），肯塔基州院长凯恩·格兰杰（Kay Granger），德克萨斯州主席罗伯特·阿德霍尔特（Robert B. Aderholt），阿拉巴马州迈克尔·辛普森（Michael K.'Chuck''Fleischmann，田纳西州David P. Joyce，俄亥俄州安迪·哈里斯，马里兰州Mark E. Amodei，内华达州内华达州David G. Valadao，加利福尼亚州丹·纽豪斯，华盛顿John R. Moolenaar，密歇根州John H. Rutherford冈萨雷斯，德克萨斯州朱莉娅·莱特洛，路易斯安那州迈克尔·克劳，德克萨斯州迈克尔·弗莱斯，密西西比Ryan K.北卡罗来纳州
国际抵达将在2025年打破记录
新加坡：世界旅游与旅游委员会（WTTC）今天透露，新加坡有望击败今年有史以来的国际到来纪录，超过了其他东南亚其他主要目的地，例如泰国和菲律宾。根据最新研究，预计2025年的国际抵达将近1600万 - 2019年大流行前水平高9.6％。印度正在助长大量旅游潮，预计到达将从2019年的11.11亿美元增长到2025年的12.5万亿美元，这是记录中最高的。尽管在全球范围内从中国出口旅行中反弹缓慢，但创纪录的中国游客将于今年前往新加坡，达到近280万，为2026年的进一步增长奠定了基础。国际到达泰国的纪录也将在今年以5％的增长范围内打破所有纪录，而菲律宾将在菲律宾以前的距离内，这将是其以前的2019年高级距离。马来西亚预计将使国际游客人数在2019年的水平上升近10％，预计将在2016年打破其先前的高峰，今年将差不多7％。WTTC总裁兼首席执行官朱莉娅·辛普森（Julia Simpson）说：“新加坡正在为全球旅游业增长，打破记录和超越地区竞争对手的步伐。。WTTC总裁兼首席执行官朱莉娅·辛普森（Julia Simpson）说：“新加坡正在为全球旅游业增长，打破记录和超越地区竞争对手的步伐。随着印度预计的访客数量高涨，中国旅行者的回归，该市的旅游引擎正以全油门运行。“这不仅是卷土重来 - 这是一个转变。新加坡在创新和可持续性领域领先，其旅游与旅游业在未来几年中的发展，驱动工作，成长和经济繁荣的情况都会比以往任何时候都更加强大。”蓬勃发展的经济引擎
