XiaoMi-AI文件搜索系统
World File Search System在量子计算机上准备开放 XXZ 链的精确特征态
相应的 Bethe 方程;后者通常难以求解。因此,尽管这些模型是“精确可解的”,但通常仍需要付出大量努力来明确计算感兴趣的物理量。量子计算机有望解决各种迄今难以解决的问题 [5,6]。这些问题包括分子和固态环境中多体系统的量子模拟 [7,8]。人们很自然地会问,量子计算机是否也能帮助解决计算量子可积模型感兴趣的物理量的问题。虽然求解 Bethe 方程仍然是一个有趣的开放性挑战 [9],但最近一个重要的进展是发现了一种用于构造精确特征态的有效量子算法 [10]。该算法可能用于明确计算相关函数,否则这是无法实现的。可积模型还可以通过为量子模拟器提供试验台来影响量子计算。尽管人们正在大力开发近期算法,如变分量子特征值求解器 (VQE) [ 11 , 12 ],以解决多体问题,但目前尚不清楚 VQE 是否能够在近期硬件上实现量子优势。另一方面,在容错量子计算机上获得一般模拟问题的量子优势被认为在量子资源方面成本极其昂贵 [ 13 – 15 ]。在嘈杂的中型量子时代 [ 16 ] 之后,早期量子计算机的可积模型的另一个好处是,它们的经典可解量可用于验证和确认目的。因此,研究特殊类别的问题(如可积模型)以更早地展示量子优势是很自然的。关键的第一步是找到解决这类问题的量子算法并量化所需的资源。 [ 10 ] 中的算法适用于闭式自旋 1/2 XXZ 自旋链,它是 Bethe [ 1 ] 求解的模型的各向异性版本 [ 17 ],是具有周期性边界条件的量子可积模型的典型例子。将量子可积性扩展到具有开放边界条件的模型也很有趣且不平凡,参见 [ 18 – 21 ] 和相关参考文献。在本文中,我们制定了一个量子算法,用于构造具有对角边界磁场的开放自旋 1/2 XXZ 自旋链的精确本征态,这是具有开放边界条件的量子可积模型的典型例子。长度为 L 的链的(铁磁)哈密顿量 H 由下式给出
金属二分法Moiré超级晶格 - CSIC数字
图S14。具有周期性边界条件(PBC)的拟定计算域。(a)顶视图和(b)由𝜃 twist的顶部MOS 2层,中间摩西2层和底部AU基板组成的异质结构系统的前视图。(c)表示内部键的表示,该键证明了双层系统中所构建的Moiré模式。moiré单位单元在(a)中以白色标记,在(c)中为红色。请注意,高𝜃双层构型导致小尺寸的Moiré周期性,𝐷。
通风对室内人体热舒适度的影响
4.5 边界条件 ................................................................................ 40 4.6 研究案例分类 .............................................................................. 43 4.7 整体质量和能量平衡 ...................................................................... 44 4.7.1 连续性方程 ...................................................................... 44 4.7.2 热力学第一定律 ...................................................................... 48 4.8 空房间模拟 ................................................................................ 50 4.8.1 入口速度的影响 ...................................................................... 50 4.8.2 入口和壁面温度的影响 ...................................................... 57 4.8.3 通风口位置的影响 ...................................................................... 60 4.9 有人的房间模拟 ............................................................................. 68 4.9.1 站立的人 ............................................................................. 68 4.9.2 坐在椅子上的人 ...................................................................... 81 4.10 热舒适区表示 ............................................................................. 85
life15 cca/es/000058
该研究基于2017年项目开始时进行的初步调查(请参阅A1.3报告)。然而,样本和边界条件差异很大,因此这两项研究之间进行的任何参考都可能带有相当大的测量误差和不确定性。尽管对初始调查进行了显着减少的记者组,但结果表明,调查的利益相关者组对气候变化有很大的兴趣,而接受采访的几乎一半涉及气候变化问题(见图1)。这个结论可能来自以下事实:各种利益相关者的调查小组密切参与了小屋的生活,因此具有环境和自然保护的重要性。
皮拉尔·费尔南德斯·皮索
本研究调查了在用于气态氢输送的钢管中使用氧气作为氢脆气相抑制剂的潜力。文中介绍了在气态氢氧混合物下进行的拉伸试验结果,分析了氧气浓度、总压力和应变速率的影响。此外,还介绍了一种数值模拟模型,该模型基于非局部 Gurson-Tvergaard-Needleman (GTN) 模型,结合氢扩散并结合“氧化层”边界条件。这项正在进行的研究的结果表明,在输送的氢气中添加少量氧气可以提高管道的耐久性。
超表面雷达单脉冲天线
摘要 — 本文介绍了用于 Ka 波段单脉冲雷达跟踪的调制超表面天线的设计、制造和测试。天线由圆形、薄接地介电层组成,该介电层由形状和大小经过调制的金属贴片纹理印刷而成。贴片层可以建模为空间可变的电容阻抗片,它与接地平板贡献一起提供整体调制电感边界条件。天线孔径被分成四个相同的角象限,每个角象限在由单个单极子发射器激发时都会辐射独立的宽边波束。四个发射器中的每一个都会激发 TM 圆柱形表面波 (SW),该波被超表面逐渐转换为漏波 (LW)。通过适当设计超表面调制,4 个子孔径被虚拟分开。为此,校准了 LW 衰减常数以充分释放每个单独的 SW,从而防止相邻区域之间的相互作用。因此,印刷结构不受任何物理分离的限制,而仅受等效边界条件的连续变化的限制。通过将源激励与简单的相位方案相结合,可获得单脉冲型线性偏振光束。值得注意的是,该解决方案不会影响结构的整体轻便性、低轮廓、馈源简单性和低制造成本,这相对于更传统的基于波导的解决方案具有固有优势。
薄层覆盖物的屈曲变形...
结构,使用实体元素来映射实验台组件,使用面元素来映射覆盖段,基于使用物理缺陷,以小值力的形式,允许正确的计算结果,证明与实验结果令人满意地一致。但必须强调的是,非线性分析是一种多价方法,结果的质量取决于边界条件映射的正确性和正确数值方法集的应用。因此,计算结果绝对应该通过适当的实验进行验证,基于设计过程中未经验证的非线性数值分析结果,导致形成不合格的结构缺陷。
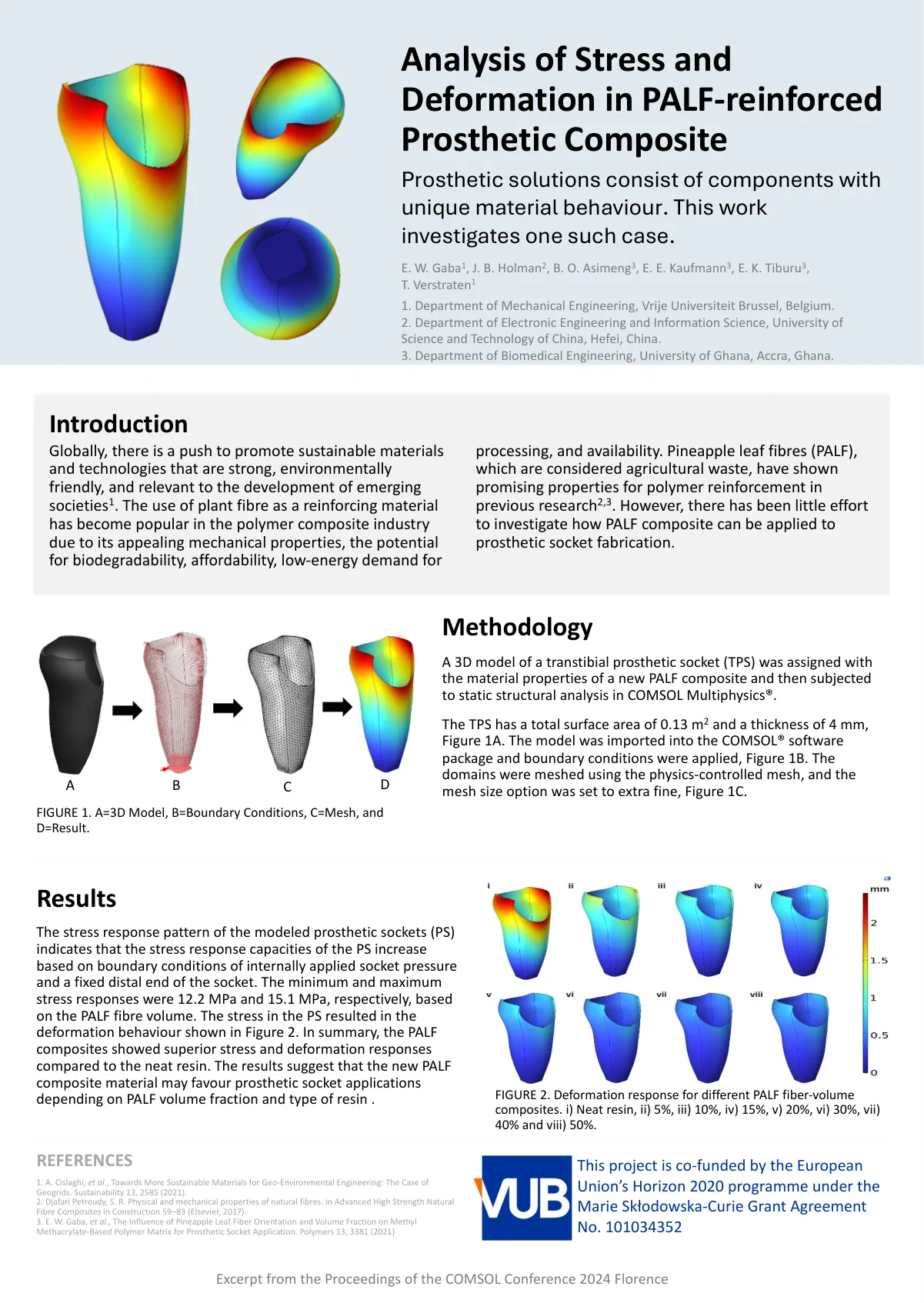
假肢解决方案由具有独特物质行为的组成部分组成。这项工作调查了一个这样的情况。
建模的假肢插座(PS)的应力响应模式表明,PS的应力响应能力基于内部施加的插座压力的边界条件和插座的固定远端。根据PALF纤维体积,最小应力反应分别为12.2 MPa和15.1 MPa。PS中的应力导致图2所示的变形行为。总而言之,与整洁的树脂相比,PALF复合材料显示出较高的应力和变形反应。结果表明,新的PALF复合材料可能会根据PALF体积分数和树脂类型而有利于假肢应用。
使用 ALTAIR SIMSOLID™ 技术概述
20 世纪初发明的用于近似解决边界值问题的 Ritz-Galerkin 方法假设近似解的函数是定义在整个相关域上的解析函数。在实际应用中,这些函数要么是三角函数,要么是无限平滑的多项式,即它们有无数个导数。此类函数有两个主要问题。首先,很难或不可能构建先验满足任意域边界上基本边界条件的函数(在结构分析中,这些条件表现为位移约束)。其次,基于此类函数构建的方程系统病态且数值不稳定,无法以足够高的精度解决实际问题。
Altair SimSolid 白皮书 - 技术概述_2019 年 2 月
20 世纪初发明的用于近似解决边界值问题的 Ritz-Galerkin 方法假设近似解的函数是定义在整个相关域上的解析函数。在实际应用中,这些函数要么是三角函数,要么是无限平滑的多项式,即它们有无数个导数。此类函数有两个主要问题。首先,很难或不可能构建先验满足任意域边界上基本边界条件的函数(在结构分析中,这些条件表现为位移约束)。其次,基于此类函数构建的方程系统病态且数值不稳定,无法以足够高的精度解决实际问题。