XiaoMi-AI文件搜索系统
World File Search System陈向阳
陈石教授的出版物：1. K. Wang，H. Li*，Z. Xu，...
9. Xu, Z.; Li, H.*; Liu, Y.; Wang, K.; Wang, H.; Ge, M.; Xie, J.; Li, J.; Wen, Z.; Pan, H.; Qu, S.; Liu,
用于系统识别和机器学习中应用的陈 - 弗利斯系列的连续性
在涉及系统识别，自适应控制和机器学习的应用程序中，随着时间的推移会不断处理输入输出数据流，以产生参数/权重估计的效率，以使假定的模型的行为与数据源相匹配。例如，在控制的背景下，这通常意味着模型的动力学应渐近地接近植物的动力学。当模型与工厂不兼容或数据流中包含不良信息时，这可能不会发生。更微妙的失败模式是模型的动力学不持续取决于参数的一种。在这种情况下，参数估计的序列可能会收敛到一定极限，而模型动力学的相应近似序列在任何意义上都无法收敛。
通过陈-西蒙斯规范理论实现德西特空间中的全息术
引言。全息术是最有前途的想法之一，它提供了量子引力的非微扰公式[1]。这种方法在反德西特（AdS）空间全息术中非常成功，即 AdS = CFT 对应[2]。另一方面，要理解现在的宇宙是如何产生的，我们需要一个德西特（dS）空间而不是 AdS 空间中量子引力的完整公式。尽管在四维高自旋引力中已经有了具体的提议[9]，并且在 dS = dS 对应[10 – 13]、全息纠缠熵[14 – 17]和 dS 静态贴片全息术[18,19]方面也取得了有趣的进展，但我们仍然缺乏对 dS 空间全息术的理解，即所谓的 dS = CFT 对应[3 – 5]（另见参考文献[6 – 8]）。尤其是，我们缺少了对偶共形场论 (CFT)，它存在于爱因斯坦引力中德西特空间的过去-未来边界上。这封信旨在为三维 dS 提出这个基本问题的解决方案。三维德西特空间的特殊之处在于它由陈-西蒙斯规范理论 [20] 描述，并且假设 dS = CFT 的标准思想，它预计与二维 CFT 对偶。S 3 上的陈-西蒙斯引力描述是德西特空间的欧几里得对应物，由一对 SU(2) 陈-西蒙斯规范理论 [20] 描述。此外，众所周知，SU(2) 陈-西蒙斯理论是
阳光植物和阴凉植物对绿光的反应有何不同？
这个实验背后的科学原理 所有植物都需要叶绿素来进行光合作用，但叶绿素并不只有一种。向阳植物的叶子中含有更多的叶绿素“a”，这是捕获光线的主要色素，可以吸收光谱两端的光线。在阴凉处生长的植物含有更多的不同色素：叶绿素“b”，它可以吸收从其他叶子反射的部分波长的光线（光谱的蓝色端）。能在阴凉处生长的植物每平方厘米的叶绿体数量也更多，叶绿体也更大，因此它们总体上可以捕获更多的光线。
人群神经科学的纵向资源
Xue-Ru Fan ( 范 雪 如 ) 1,2,3,† , Yin-Shan Wang ( 王 银 山 ) 1,3,4,† , Da Chang ( 常 达 ) 1,3,† , Ning Yang ( 杨 3 宁 ) 1,2,3,4 , Meng-Jie Rong ( 荣 孟 杰 ) 1,2,3,4 , Zhe Zhang ( 张 吉吉 ) 5 , Ye He ( 何 叶 ) 6 , Xiaohui Hou ( 侯 4 晓晖 ) 7 , Quan Zhou ( 周 荃 ) 1,2,3 , Zhu-Qing Gong ( 宫 竹 青 ) 1,2,3 , Li-Zhi Cao ( 曹 立 智 ) 2,4 , Hao-Ming 5 Dong ( 董 昊 铭 ) 1,4,8,9 , Jing-Jing Nie ( 聂 晶晶 ) 1,3 , Li-Zhen Chen ( 陈 丽 珍 ) 1,3 , Qing Zhang ( 张 6 青 ) 2,4 , Jia-Xin Zhang ( 张 家 鑫 ) 2,4 , Hui-Jie Li ( 李 会 杰 ) 2,4 , Min Bao ( 鲍 敏 ) 2,4 , Antao Chen ( 陈 安 7 涛 ) 10,11 , Jing Chen ( 陈 静 ) 12,13 , Xu Chen ( 陈 旭 ) 11 , Jinfeng Ding ( 丁 金 丰 ) 2,4 , Xue Dong ( 董 雪 ) 2,4 , 8 Yi Du ( 杜 忆 ) 2,4 , Chen Feng ( 冯 臣 ) 2,4 , Tingyong Feng ( 冯 廷 勇 ) 11 , Xiaolan Fu ( 傅 小 兰 ) 2,14 , 9 Li-Kun Ge ( 盖 力 锟 ) 2,4 , Bao Hong ( 洪 宝 ) 12,15 , Xiaomeng Hu ( 胡 晓 檬 ) 16 , Wenjun Huang ( 黄 文 10 君 ) 12,15 , Chao Jiang ( 蒋 超 ) 17 , Li Li ( 李 黎 ) 12,13 , Qi Li ( 李 琦 ) 17 , Su Li ( 李 苏 ) 2,4 , Xun Liu ( 刘勋 ) 2,4 , 11 Fan Mo ( 莫 凡 ) 2,14 , Jiang Qiu ( 邱 江 ) 11 , Xue-Quan Su ( 苏 学 权 ) 7 , Gao-Xia Wei ( 魏 高 峡 ) 2,4 , 12 Yiyang Wu ( 吴 伊 扬 ) 2,4 , Haishuo Xia ( 夏 海 硕 ) 11 , Chao-Gan Yan ( 严 超赣 ) 2,4 , Zhi-Xiong Yan ( 颜 13 志 雄 ) 7 , Xiaohong Yang ( 杨 晓 虹 ) 16 , Wenfang Zhang ( 张 文 芳 ) 2,4 , Ke Zhao ( 赵 科 ) 2,14 , Liqi Zhu 14 ( 朱 莉 琪 ) 2,4 , Lifespan Brain Chart Consortium (LBCC) * , Chinese Color Nest Consortium 15 (CCNP) ** , and Xi-Nian Zuo ( 左 西 年 ) 1,2,3,4,7,18,*** 16
立法会FC164/2024号文件立法会财务委员会会议纪要日期...
李惟宏议员李梓敬议员李镇强议员, JP 狄志远议员, SBS, JP 吴秋北议员, SBS, JP 吴杰庄议员, MH, JP 周小松议员周文港议员, JP 林振升议员林素蔚议员林琳议员林筱鲁议员, SBS, JP 姚柏良议员, MH, JP 洪雯议员梁子颖议员, MH 梁文广议员, MH 梁熙议员梁毓伟议员, JP 陈月明议员, MH 陈仲尼议员, SBS, JP 陈沛良议员陈勇议员, SBS, JP 陈祖恒议员陈家珮议员, MH, JP 陈绍雄议员, JP 陈凯欣议员陈颖欣议员陈学锋议员, MH, JP 张欣宇议员郭玲丽议员陆瀚民议员黄英豪议员, BBS, JP 黄俊硕议员黄国议员, BBS, JP 杨永杰议员管浩鸣议员, BBS, JP 邓飞议员, MH 邓家彪议员, BBS, JP 黎栋国议员, GBS, IDSM, JP 刘智鹏议员, BBS, JP
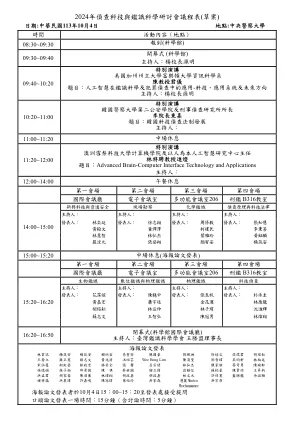
2024年侦查科技与鉴识科学研讨会议程表(草案)
海报論文发表林韦志杨筑安杨筑安赖欣宜易哲安陈国豪邓珮琳徐培文侯儒君胡瑄耘王乔立苏正宪苏志文黄兆清洪翊芸Wee Beng Lim 陈淯圣郭哲玮吴昀轩林柏廷宋泓葰柯虹瑩林政宏林奕全张馨呂宗谚林弘杰陈家维蔡奇男陈瑜轩孙德娟林子桓邱景徽陈祺蔡世国谢立伟翁颖信苏柏豪陈韦佑王升钧洪孟君胡家豪陈羽蓁林炜翔胡政嘉胡政嘉林文元许倬宪藍锦龍余滋雅褚祥蕴洪晨玮许嘉峻陈冠玮葉怡伶吴家森慧麗Mintra Phochanamanee 吴宗原
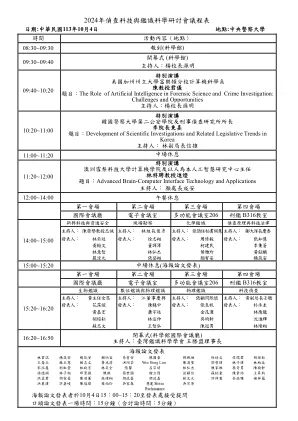
2024年侦查科技与鉴识科学研讨会议程表
海报論文发表林韦志杨筑安杨筑安赖欣宜易哲安陈国豪邓珮琳徐培文侯儒君胡瑄耘王乔立苏正宪苏志文黄兆清洪翊芸Wee Beng Lim 陈淯圣郭哲玮林子玮林柏廷宋泓葰柯虹瑩林政宏林奕全张馨呂宗谚林弘杰陈家维蔡奇男陈瑜轩孙德娟林子桓邱景徽陈祺蔡世国谢立伟翁颖信苏柏豪陈韦佑王升钧洪孟君胡家豪陈羽蓁林炜翔胡政嘉胡政嘉林文元许倬宪余滋雅褚祥蕴洪晨玮许嘉峻陈冠玮葉怡伶吴家森慧麗Mintra Phochanamanee 吴宗原
用于短距离 400G–1.6T 光互连的 100 Gb/s PAM-4 VCSEL 驱动器和 TIA
路东来 1, 2 , 何健 1, 4 , 李伟忠 5 , 陈斯凯 1 , 刘健 1, 3 , 吴南健 1, 2, 3 , 于宁美 4 , 刘丽媛 1, 2, 3 , 陈勇 6 , 习晓 5 和 南琪 1, 3