XiaoMi-AI文件搜索系统
World File Search System随机过程
机器学习中的生成模型：原理和效率
（3）深层生成模型求解随机过程：研究求解随机模型（例如扩散模型）（例如扩散模型）（例如，扩散模型）中随机过程的随机微分方程（SDE）或部分微分方程（PDE）（PDE）（PDES）。模型）在培训期间（5）生成模型中的隐式偏见和正则化：探索生成模型中存在的隐式偏见及其对概括的影响。研究显式和隐式正则化技术的有效性（6）生成模型的鲁棒性和泛化边界：分析生成模型的鲁棒性界限及其在分布分布的场景下（7）潜在的空间几何形状（7）潜在的空间几何学和流形学习：分析与生成模型的潜在空间和与生成数据分配的分析及其关系分配的相关性。探索如何平衡潜在空间中的多样性和发电质量，并研究复杂数据情景中不同流形学习技术的有效性和局限性
扩散模型第1章：倒数时间SDE
其中𝑋𝑋，𝑓𝑋𝑓𝑋，𝑡∈ℝ，𝑔𝑡∈ℝ××𝑑×𝑑×𝑑×𝑑×𝑊是一个二二维的布朗尼运动或维也纳过程。𝑋𝑡𝑡是一个随机过程。（我们可以允许𝑔也取决于𝑋𝑡，但这使得方程更加复杂。）
![arXiv:2212.03796v3 [quant-ph] 2024 年 10 月 4 日](/simg/5\556eb4fe5062250c9ddec40d867b5a857c06018f.webp)
arXiv:2212.03796v3 [quant-ph] 2024 年 10 月 4 日
在本文中，我们应用量子信道和开放系统状态演化的理论，提出了一种用于量子隐马尔可夫模型 (QHMM) 的酉参数化和高效学习算法。我们将任何具有非平凡算子和表示的量子信道视为具有隐藏动态和可测量发射的随机系统。通过利用量子信道更丰富的动态，特别是通过混合状态，我们证明了量子随机生成器比经典生成器具有更高的效率。具体而言，我们证明了可以在量子希尔伯特空间中使用比经典随机向量空间少二次的维度来模拟随机过程。为了在量子硬件上的电路计算模型中实现 QHMM，我们采用了 Stinespring 的扩张构造。我们表明，可以使用具有中间电路测量的量子电路有效地实现和模拟任何 QHMM。在酉电路的假设空间中，可行的 QHMM 学习的一个关键优势在于 Stinespring 扩张的连续性。具体而言，如果通道的酉参数化在算子范数中接近，则相应通道在钻石范数和 Bures 距离中也将接近。此属性为定义具有连续适应度景观的高效学习算法奠定了基础。通过采用 QHMM 的酉参数化，我们建立了一个正式的生成学习模型。该模型形式化了目标随机过程语言的经验分布，定义了量子电路的假设空间，并引入了一个经验随机散度度量——假设适应度——作为学习成功的标准。我们证明，该学习模型具有平滑的搜索景观，这归因于 Stinespring 扩张的连续性。假设空间和适应度空间之间的平滑映射有助于开发高效的启发式和梯度下降算法。我们考虑了四种随机过程语言的例子，并使用超参数自适应进化搜索和多参数非线性优化技术训练 QHMM，这些技术应用于参数化的量子拟设电路。我们通过在量子硬件上运行最优电路来确认我们的结果。
M.Tech（PT）电源电子学教学大纲2021.pdf
CO1: Develop mathematical model and analyse engineering problems CO2: Apply linear programming concepts to solve real life problems CO3 : Formulate and solve complex engineering problems using non programming techniques CO4 : Analyse and solve stochastic engineering problems Module 1: Vector spaces, subspaces, Linear dependence, Basis and Dimension, Linear transformations, Kernels and Images , Matrix representation of linear transformation, Change of basis, Eigen线性运算符模块的值和特征向量2线性编程问题的数学公式，单纯形方法，线性编程中的双重性，双单纯形方法。模块3非线性编程初步，不受约束的问题，搜索方法，斐波那契搜索，金段搜索，搜索，约束问题，拉格朗日方法，库恩 - 塔克条件4随机变量，分布和密度和密度功能，矩和矩和瞬间的功能，自动变量和状态分布，条件分布，条件分布，条件分布，条件分布，条件分布，构图，构成，构造，构成了构图，构成了构图，构成了构图，构成了构图，构成了构图，构成了序列，构成了构图，构成了构图，构成了构图，构成了构图，构成了构图过程。教科书和参考文献1。J.C. PANT：优化概论，Ja那教兄弟，新德里，2014年2。S.S. Rao：优化理论与应用，新时代，新德里，2012年3月3日肯尼斯·霍夫曼（Kenneth Hoffman）和雷·库兹（Ray Kunze），线性代数，第2版，皮尔逊，2015年2。Erwin Kreyszig，使用应用的入门功能分析，John Wiley＆Sons，2004。3。Irwin Miller和Marylees Miller，John E. Freund的数学统计，第6 Edn，Phi，2002年。4。约翰·B·托马斯（John B Thomas），《应用概率和随机过程简介》，约翰·威利（John Wiley），2000Roy D Yates，David J Goodman，“概率和随机过程”，第2版，Wiley India，2011年5。爸爸，概率，随机变量和随机过程，第三版，麦格劳山，2002 6。
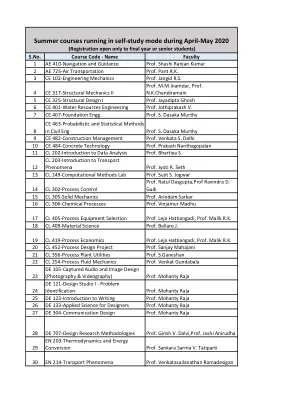
2020 年 4 月至 5 月期间以自学模式开设的暑期课程
107 EE 325-概率和随机过程教授Gaurav S. Kasbekar 108 EE 328-数字通信教授Kumar Appaiah 109 EE 334-电力系统教授Kulkarni AM 110 EE 338-数字信号处理教授Gadre VM 111 EE 602-雷达系统教授Kushal R. Tuckley 112 EE 609-辐射系统教授库沙尔·R·塔克利
秋季2024年研究生课程描述
数学526/Stats 526。离散状态随机过程Cohen，ASAF T/T t/t Th 10:00 AM-11：30 AM Cohen，ASAF T/TH 11:30 AM-1：00 PM TBD T/TH T/TH 8:30 AM-10：00 AM MATH 525或Stats 525或STAT 525或EEC 525或EECS 525或EECS 501。（3）。（BS）。可能不会重复以获得信用。这是关于随机过程在离散状态空间上的理论和应用的课程。一些特定主题包括：（1）马尔可夫链 - 马尔可夫属性， - 复发和瞬态， - 平稳性， - 千古， - 耦合， - 退出概率和预期的退出时间； （2）马尔可夫决策过程 - 最佳控制， - Banach固定点定理； （3）指数分布和泊松过程 - 无内存的特性， - 变薄和叠加， - 复合泊松过程； （4）Markov连续时间 - 发电机和Kolmogorov方程， - 嵌入了马尔可夫链， - 固定分布并限制定理， - 退出概率和预期的退出时间， - 马尔可夫队列； （5）Martingales - 有条件的期望， - 与Martingales的赌博（交易）， - 可选采样， - 用于计算退出概率和预期退出时间的应用， - Martingale Convergence。
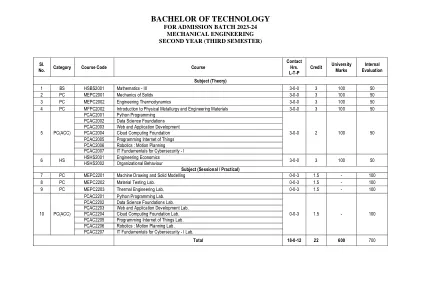
技术学士
模块5：应用统计（8小时）随机抽样，参数估计，最大似然估计，置信区间。回归和相关分析：直线的拟合（避免正方形的方法），与基本属性相关系数。教科书：1。E. Kreyszig的高级工程数学，John Willey＆Sons Inc.第10版。2。Ronald E. Walpole，Raymond H. Myers，Sharon L. Myers＆Keying Ye，“工程师与科学家的概率与统计数据”，第八版，2007年，新德里Pearson Education Inc.。 参考书：1。 J. Sinha Roy和S. Padhy，Kalyani出版商的普通和部分微分方程。 2。 B. V. Ramana的高级工程数学，McGraw Hill Education。 3。 PAL和S. Bhunia的工程数学，牛津出版物。 随机过程，Roy D. Yates，Rutgers和David J. Goodman，John Wiley and Sons，Inc。Ronald E. Walpole，Raymond H. Myers，Sharon L. Myers＆Keying Ye，“工程师与科学家的概率与统计数据”，第八版，2007年，新德里Pearson Education Inc.。参考书：1。J. Sinha Roy和S. Padhy，Kalyani出版商的普通和部分微分方程。2。B. V. Ramana的高级工程数学，McGraw Hill Education。3。PAL和S. Bhunia的工程数学，牛津出版物。随机过程，Roy D. Yates，Rutgers和David J. Goodman，John Wiley and Sons，Inc。
ELEC3810 神经工程数据科学（2023 年秋季...
这是一门数据科学在神经工程中应用的入门课程。本课程将介绍数据科学的基本原理、概率和统计估计的技术和实现，以及神经工程中几个实际问题的建模。主题包括概率、随机变量、统计检测和估计、随机过程、神经系统的结构和功能、编码和解码、群体编码、神经网络、可塑性和学习、神经接口和康复。将介绍概率、随机过程和估计的概念，以便学生能够理解和实现神经工程的真实示例，并认识到最新技术的影响。本课程将增强学生的视野，鼓励他们在未来的跨学科研究领域工作。学生有望通过脑机接口项目获得数据科学和神经科学的知识以及实践经验。本课程包含计算神经科学的元素及其在神经工程中的应用，神经工程是生物医学工程的一个重要领域，适合具有 CBE 背景的学生。它还包含数据科学和神经工程应用的元素，因此，它也适合来自 ECE 的学生。不同课程代码的学生将获得相同待遇，只使用一套课程内容和考核安排。先修课程：（MATH2111 或 MATH 2121）和 MATH 2421，或 BIEN 2310 或 BIEN 3320 成绩基于家庭作业（20%）、期中考试（30%）和期末项目（50%）。暂定时间表如下。
我们生活在一个科学的世界，从数学开始......
ICTS 教员 Subhro Bhattacharjee 凝聚态物理学：强关联系统 Chandan Dasgupta（西蒙斯客座教授） 凝聚态物理学和统计力学 Abhishek Dhar 非平衡统计力学 Deepak Dhar（INSA 杰出教授） 统计力学 Hulikal Krishnamurthy（西蒙斯客座教授） 凝聚态理论 Manas Kulkarni 凝聚态和统计物理学 Anupam Kundu 统计物理学、随机过程 Sumathi Rao（ICTS 杰出高级教授） 凝聚态物理学 Sthitadhi Roy 凝聚态物理学和统计力学 Joseph Samuel（西蒙斯客座教授） 广义相对论、量子信息、物理学中的几何和拓扑