XiaoMi-AI文件搜索系统
World File Search System妊娠糖尿病患者的治疗水平
抽象怀孕是一种生理现象,涵盖了许多变化,主要变化涉及女性代谢。鉴于此,众所周知,某些变化导致妊娠过程不规则,从而导致孕产妇和胎儿二项式的并发症,干扰和死亡的机会更大,从而确定了所谓的高风险怀孕。在各种疗效中,有妊娠糖尿病(DMG),通过进行治疗的有效性导致降低怀孕期间和妊娠后可能的不利结果。因此,这项研究旨在通过应用有关遵守DMG诊断妇女治疗水平的调查表进行定量调查,并确定了阻止她们在Cascavel/PR市的高风险妊娠门诊诊所中鉴定其是否足够的主要因素。42名妇女是从一般问卷,莫里斯基绿色测试和自我护理活动问卷调整的适用中采访的。通常,有效地发生了饮食,药物疗法和血糖监测的粘附和成就,表达了统计学意义的价值(> 50%)。另一方面,体育锻炼是具有较少粘附和日常成就的支柱。此外,有可能得出结论,财务状况和工作是指出某些因果因素的参与者中有效的治疗性非辅助 - 顾问的主要原因。关键词:妊娠糖尿病;治疗;遵守治疗。抽象怀孕是一种生理现象,涵盖了许多变化,主要变化是涉及女性代谢的主要变化。鉴于这一点,众所周知,某些改变导致了不规则的妊娠过程,从而导致产妇二项式的并发症,干扰和死亡的机会更大,从而确定了所谓的高风险妊娠。在各种疗法发生中,有妊娠糖尿病(GDM),通过其治疗的有效性,妊娠糖尿病会导致妊娠期间和怀孕后可能的不利结果降低。因此,这项研究旨在通过在遵守诊断为GDM的妇女治疗的水平以及鉴定的主要因素中应用问卷,以防止在Cascavel/PR的高风险中鉴定出足够的怀孕门诊门诊诊所的主要因素。根据一般问卷的应用,莫里斯基绿色的测试和自我保健活动问卷调整的适应,对42名妇女进行了采访。通常,对饮食和药物疗法和血糖监测的遵守和实施有效地发生了,表达了统计学意义的价值(> 50%)。另一方面,体育锻炼是具有最低依从性和日常表现的支柱。此外,可以得出结论,财务状况和工作是未遵循指示某些因果因素的参与者有效治疗的主要原因。关键词:妊娠糖尿病;治疗;遵守治疗。
非...的确定性高斯转换协议
在连续变量量子技术的背景下,高斯状态和操作通常被视为自由可用的,因为它们相对容易通过实验获得。相比之下,非高斯状态的生成以及非高斯操作的实施则带来了重大挑战。这种分歧促使人们引入非高斯性的资源理论。对于任何资源理论,确定资源之间的自由转换协议(即非高斯状态之间的高斯转换协议)具有实际意义。通过系统的数值研究,我们通过任意确定性的一对一模式高斯映射解决了实验相关的单模非高斯状态之间的近似转换。首先,我们表明,对于有限能量,猫状态和二项式状态大致等效,而这种等效性以前仅在无限能量极限下才为人所知。然后,我们考虑从光子增加和光子减少的压缩态生成猫态,通过引入额外的压缩操作来改进已知方案。我们开发的数值工具还允许人们设计出三压缩态到立方相态的转换,超越之前报道的性能。最后,我们确定了其他各种不可行的转换。
bardic:强大的峰要求RNA-DNA相互作用数据
染色质相关的非编码RNA通过靶向基因组基因座在各种细胞过程中起重要作用。存在两种类型的全基因组NGS实验来检测此类靶标:“一到全部”,该目标的重点是单个RNA的靶标和“全能”,该目标捕获了样本中所有RNA的靶标。与许多NGS实验一样,它们容易出现偏见和噪声,因此检测“峰” - RNA与基因组靶标的特定相互作用至关重要。在这里,我们提出了Bardic - 二项式RNA-DNA相互作用调用器 - 一种量身定制的方法,可检测两种类型的RNA-DNA相互作用数据中的峰值。Bardic是同时考虑数据中两个最突出的偏见的第一个工具:染色质异质性和相互作用频率的距离衰减。由于RNA的相互作用偏好不同,因此根据单个RNA的丰度和接触模式,Bardic适应了峰值大小。这些功能使Bardic能够比当前应用的峰值呼叫算法做出更强大的预测,并更好地处理全部数据的特征性稀疏性。Bardic软件包可以在https://github.com/dmitrymyl/bardic上免费获得。
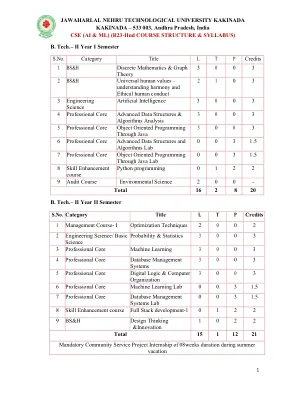
533 003,安得拉邦,印度 CSE(AI 和 ML)(R23-...
(L1) 第一单元:数理逻辑:命题演算:语句和符号、联结词、合式公式、真值表、同义反复、公式等价性、对偶律、同义反复蕴涵、范式、语句演算的推理理论、前提的一致性、间接证明方法、谓词演算:谓词、谓词逻辑、语句函数、变量和量词、自由和有界变量、谓词演算的推理理论。第二单元:集合论:集合:集合上的运算、包含-排斥原理、关系:性质、运算、分割和覆盖、传递闭包、等价性、兼容性和偏序、哈斯图、函数:双射、组合、逆、排列和递归函数、格及其性质。第三单元:组合学和递归关系:计数基础、排列、重复排列、循环和限制排列、组合、限制组合、二项式和多项式系数和定理。递归关系:生成函数、序列函数、部分分式、计算生成函数系数、递归关系、递归关系公式、通过代换和生成函数解决递归关系、特征根法、解决非齐次递归关系
RNA- ...
RNA测序(RNA-SEQ)已成为转录组学的基石,为各种生物条件和样品类型的基因表达提供了详细的见解。然而,RNA-Seq数据通常受到批处理效应的影响,这是系统的非生物学差异,会损害数据可靠性并掩盖真实的生物学变异。为了应对这些挑战,我们引入了战斗-REF,这是一种精致的批次效应校正方法,可增强RNA-Seq数据中差异表达分析的统计能力和可靠性。在战斗seq的基础上构建,战斗-REF采用负二项式模型来调整计数数据,但通过对整个批处理的汇总分散参数进行创新,并保留参考批次的计数数据。我们的方法在模拟环境和实际数据集中都表现出了卓越的性能,例如生长因子受体网络(GFRN)数据和NASA GenElab转录组数据集,从而显着提高了对现有方法的敏感性和特异性。通过有效缓解批处理效应,同时保持高检测能力,Combat-Ref被证明是增强RNA-SEQ数据分析的准确性和解释性的强大工具。
低SNR环境中卫星跟踪算法的性能分析
处理多个帧的算法对于在较大范围搜索中识别昏暗的卫星信号和轨道运动至关重要。检测方法之前,要查看具有目标信号并将所有帧数据提供给跟踪器的多个图像,并将检测决策延迟直至形成轨道。本文旨在通过对所有帧进行二项式决策规则进行建模,以估算低SNR跟踪算法的性能。作为系统设计分析的一部分,有必要根据各种参数来预测搜索的性能,例如光圈,传输,检测器灵敏度,帧数,最小可检测的目标大小,衰减和其他因素。这些搜索算法的性能可以由Monte Carle(MC)模拟确定,该模拟需要许多迭代来创建表来描述预期的系统性能。不幸的是,当系统参数和目标特性变化导致任务延迟时,这些基于MC的预测可能需要大量返工。这项工作旨在描述一个分析表达式,以描述场景的预期检测和虚假警报性能,该表达式将允许在太空域名(SDA)任务中观察平台的搜索和收集任务。另外,分析表达可以直接通过对结果的主动性理解并更好地理解任何操作异常。
ISSN: 2320-5407 国际J. Adv. Res. 13(01), 12-40
该项目旨在开发一款安全的应用程序,利用量子、计算和谷歌量子人工智能,重点关注可持续性。该应用程序将采用先进的加密技术,包括异或门信号处理和控制工程二项式 z 变换方法,以确保强大的安全性并有效防止网络犯罪。该应用程序将由可再生能源供电,特别是太阳能、水力发电和风力涡轮机。这些可再生能源将与量子处理器集成,利用人工智能预测优化控制来有效管理能源消耗并最大限度地提高性能。这种集成确保应用程序以峰值效率运行,同时最大限度地减少其碳足迹。例如,量子处理器的运行可以优化以与可再生能源的可用性保持一致。在日照高峰时段,太阳能电池板可以为量子处理器提供充足的电力,而人工智能系统则相应地预测和调整处理器的工作负载。同样,可以监控和管理水力发电和风力涡轮机产生的电力以提供稳定的能源,确保量子处理器即使在可再生能源供应波动时也能保持高效率。总体而言,该项目代表了量子计算与可持续实践相结合的开创性努力,旨在为现代加密挑战提供安全且环保的解决方案。
统计学应用第三版(Kathryn Kozak 著)
为此,我要求学生解释他们的计算结果。我结合使用技术(R Studio)进行大多数计算。正因为如此,你不会发现我使用任何标准差或相关性和回归的计算公式,因为我希望学生理解这些数量的概念。此外,因为我使用技术,所以你不会在书中找到标准正态表、学生 t 表、二项式表、卡方分布表和 F 分布表。本书与其他统计学书籍的另一个区别是假设检验和置信区间的顺序。大多数书籍首先介绍置信区间,然后介绍假设检验。我发现先介绍假设检验,然后再介绍置信区间对学生来说更容易理解。最后,我不再强调 z 检验的使用。事实上,我只用它来介绍假设检验,再也不用它了。应该强调两个样本而不是一个样本的检验。最后,为了帮助学生理解和激发兴趣,大多数作业和示例都使用具有多个变量的真实数据。多个变量的好处在于,你可以要求学生研究具有不同变量的不同分析。这样,学生就可以处理数据,并提出问题和使用数据回答问题的联系。再次,我希望你发现这本书对你的入门统计学课程有用。
考试问题机器人技术和人工智能
1。控制系统设计。控制系统和系统配置的基本组件。2。系统的标准数学模型:输入输出模型,状态空间模型。3。动态系统线性化,并评估雅各布基质。4。框图转换:系列,并行和反馈连接。5。系统的结构特性:可控性和可观察性。6。一阶和二阶系统:传输功能,步骤响应,冲动响应。7。连续时间系统的稳定性:定义,S-平面根位置,Routh-Hurwitz稳定性标准。8。Lyapunov确定连续时间系统稳定性的方法。9。Nyquist稳定性标准。时间延迟系统的稳定性。10。系统的性能特征(规格):过冲,沉降时间,稳态误差,相对稳定性,阻尼比。11。稳态准确性。具有不同类型编号(集成数)的Unity反馈控制系统中的稳态错误。12。标准特征多项式:Butterworth多项式,二项式多项式。13。通过模态控制(POL放置)对线性系统的稳定。 14。 连续时间系统(Luenberger观察者)的全顺序和降低状态观察者。通过模态控制(POL放置)对线性系统的稳定。14。连续时间系统(Luenberger观察者)的全顺序和降低状态观察者。
B.Tech Power电子和仪器
模块1:线性代数简介(8个讲座)向量,向量空间,线性独立性,碱基和维度,正交性,线性图和矩阵,矩阵的基本子空间,rank-nullity Theorem。模块2:光谱分解(6个讲座)特征值,不变子空间,内部产物,规范,正统碱基,光谱定理,等法,极值和奇异值分解,应用。模块3:矩阵(5个讲座)特殊矩阵,规范和决定因素的特性。模块4:概率简介(6个讲座)经典和公理概率,概率空间,条件概率和独立性,总概率,贝叶斯规则。模块5:随机变量(8个讲座)定义,常见示例,累积分布函数,概率质量函数,概率密度函数;随机变量的函数;期望 - 卑鄙,差异和时刻;特征和瞬间的功能;特殊的随机变量 - 二项式,泊松,统一,指数和高斯;共同时刻,有条件的期望;协方差和相关性 - 独立,不相关和正交随机变量;两个随机变量的函数;大量法律和中央限制定理的法律薄弱。模块6:随机过程简介(3个讲座)离散和连续时间过程;随机过程的概率结构;卑鄙,自相关和自相关功能;随机过程的示例:白噪声。文本/参考书: