XiaoMi-AI文件搜索系统
World File Search System特征值
R22 B.Tech. CSE（网络安全）课程大纲
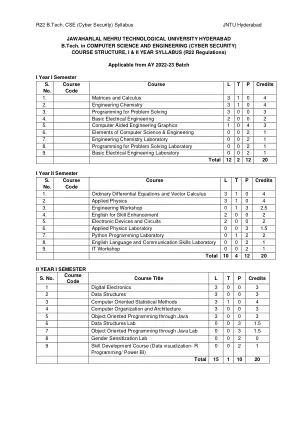
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I：矩阵 10 L 通过梯形和标准形式对矩阵进行秩，通过高斯-乔丹方法对非奇异矩阵进行逆运算，线性方程组：用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元：特征值和特征向量 10 L 线性变换和正交变换：特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理（无证明）、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元：微积分 10 L 均值定理：罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积（仅限于笛卡尔坐标系）、不当积分的定义：Beta 函数和 Gamma 函数及其应用。第四单元：多元微积分（偏微分和应用）10 L 极限和连续性的定义。偏微分：欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用：使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
M.Tech控制工程 /控制系统< / div>
编写一组线性方程的矩阵表示，并分析方程系统的解决方案查找特征值和本征媒介使用正交转换将二次形式减少到规范形式。分析序列和序列的性质。在平均值定理上求解应用程序。使用beta和伽马函数评估不正确的积分找到两个具有/没有约束的变量的功能的极端值。单元I：矩阵矩阵：矩阵的类型，对称；隐士偏度对称；偏斜;正交矩阵；单一矩阵；按梯形形式和正常形式的矩阵等级，高斯 - 约旦方法的非单个矩阵倒数；线性方程系统；解决同质和非均匀方程的求解系统。高斯消除方法；高斯Seidel迭代方法。单元-II：特征值和本征载体线性变换和正交转换：特征值和特征向量及其特性：矩阵的对角线化； Cayley-Hamilton定理（没有证据）；查找矩阵的逆向和力量由Cayley-Hamilton定理进行；二次形式的二次形式和性质；通过正交转换单位-III将二次形式的形式降低至规范形式：序列与串联序列：序列的定义，极限；收敛，发散和振荡序列。系列：收敛，发散和振荡系列；一系列积极术语；比较测试，p检验，D-Alembert的比率测试； Raabe的测试；库奇的整体测试；库奇的根测试；对数测试。泰勒的系列。交替系列：Leibnitz测试；交替收敛序列：绝对和有条件收敛。单元-IV：微积分平均值定理：Rolle的定理，Lagrange的平均值定理，其几何解释和应用，Cauchy的平均值定理。
密度矩阵
密度矩阵在量子力学中用于给出量子系统的部分描述，其中省略了某些细节。例如，在由两个或多个子系统组成的复合量子系统中，人们可能会发现，只构造其中一个子系统的量子描述很有用，无论是在单个时间还是作为时间函数，而忽略其他子系统。或者，量子系统的确切初始状态未知，人们希望使用概率分布或预概率作为初始状态。概率分布用于经典统计力学以构造部分描述，密度矩阵在量子统计力学中起着类似的作用，这超出了本书的范围。在本章中，我们将提到密度矩阵在量子理论中的几种使用方式，并讨论它们的物理意义。正算子和密度矩阵在第 3.9 节中定义。概括地说，正算子是特征值非负的 Hermitian 算子，密度矩阵 ρ 是迹（特征值之和）为 1 的正算子。如果 R 是正算子但不是零算子，则其迹大于零，并且可以通过公式定义相应的密度矩阵
基于快速检测纸板
摘要：长期以来，农药残留物一直是食品安全的重要方面，这一直是一个主要的社会问题。这项研究对基于酶抑制方法鉴定农药残留物快速检测卡的研究和分析进行了研究和分析。在这项研究中，图像识别技术用于从快速检测卡的检测结果中提取颜色信息RGB特征值，并建立了四个回归模型，以定量预测使用RGB特征值快速检测卡指示的农药残留浓度。四个回归模型是线性回归模型，二次多项式回归模型，指数回归模型和RBF神经网络模型。通过研究和比较，已经表明，指数回归模型在预测快速检测卡指示的农药残留浓度方面表现出色。相关值为0.900，均方根误差为0.106。当预期浓度接近0时，不会有负预测值。这为基于酶抑制方法的农药残留物快速检测卡开发图像识别设备的开发提供了一种新颖的概念和数据支持。
Virginie Ehrlacher（加兰德）
· Athmane Bakhta、Virginie Ehrlacher，《具有非零通量和移动边界条件的交叉扩散系统》，已接受在 ESAIM：M2AN 上发表。 · Virginie Ehrlacher 和 Damiano Lombardi，《用于解决 Vlasov-Poisson 系统的动态自适应张量方法》，《计算物理杂志》，339，2017 年，第 285-306 页。 · Virginie Ehrlacher、Christoph Ortner 和 Alexander V. Shapeev，《晶体缺陷原子模拟的边界条件分析》，ARMA，222(3)，2016 年，第 1217-1268 页。 · Eric Cancès、Virginie Ehrlacher、Frédéric Legoll 和 Benjamin Stamm，近似椭圆方程均匀系数的嵌入式校正器问题，Comptes-Rendus Mathématiques，353(9)，2015，第 801-806 页。 · Eric Cancès、Virginie Ehrlacher 和 Tony Lelièvre，高维特征值问题的贪心算法，构造逼近，40，2014 年，第 387-423 页。 · Eric Cancès、Virginie Ehrlacher 和 Yvon Maday，《自伴特征值问题的非一致近似：应用于超胞方法》，《Numerische Mathematik》，128，2014 年，第 663-706 页。
活化过程的变分量子特征解法
摘要 随机过程理论影响着物理和社会科学。在分子尺度上，由于热波动，随机动力学无处不在。福克-普朗克-斯莫鲁霍夫斯基方程模拟了扩散区域中选定自由度的概率密度随时间的变化，因此它是物理化学中的主力。在本文中，我们报告了变分量子特征值求解器的开发和实现，以解决福克-普朗克-斯莫鲁霍夫斯基特征值问题。我们表明，这种通常用于解决量子化学问题的算法可以有效地应用于经典系统，为量子计算机的新应用铺平了道路。我们计算了具有最近邻相互作用的线性转子链中的构象转变速率。我们提供了一种在量子计算机上对链的给定构象的概率分布进行编码的方法，并评估了其在操作方面的可扩展性。对小链的噪声量子模拟器和量子设备（IBMQ Santiago）进行了性能分析，结果显示无需进一步添加任何错误缓解技术，与经典基准结果一致。
量子信息处理简介 讲座 26
纠缠的另一个度量是负性。负性没有操作解释（或至少没有标准解释），但与以前的度量不同，它很容易计算。部分转置 ρ TA 是一个正但不完全正的映射。因此它不是物理运算，但我们可以用数学方法来完成。具体而言，由于它是正的，当你将部分转置应用于张量积状态时，你会得到一个正状态。但是，由于它不是完全正的，如果你将它应用于某些纠缠态，你会得到具有“密度矩阵”负特征值的“状态”。负特征值的总和就是状态的负性。它是纠缠单调的，而且它是可加的并且易于计算。然而不幸的是，负性并不忠实。有些状态具有 0 负性但不可分离。实际上，这样的状态一定是束缚纠缠态（这就是我们知道束缚纠缠态存在的原因），因为成功的蒸馏过程会产生最大纠缠态，其负性不为零。由于负性在 LOCC 下无法增加，因此不可能实现这样的协议。
![b'我们提出了一系列量子算法，用于计算各种量子熵和距离，包括冯·诺依曼熵、量子 R\xc2\xb4enyi 熵、迹距离和 \xef\xac\x81delity。所提出的算法在低秩情况下的表现明显优于最知名的（甚至是量子的）算法，其中一些算法实现了指数级加速。特别是，对于秩为 r 的 N 维量子态，我们提出的用于计算冯·诺依曼熵、迹距离和 \xef\xac\x81delity（加性误差 \xce\xb5 内）的量子算法的时间复杂度为 \xcb\x9c O r 2 /\xce\xb5 2 、 \xcb\x9c O r 5 /\xce\xb5 6 和 \xcb\x9c O r 6 。 5 /\xce\xb5 7 . 5 1 。相比之下，已知的冯·诺依曼熵和迹距离算法需要量子时间复杂度为 \xe2\x84\xa6( N ) [AISW19,GL20,GHS21]，而最著名的 \xef\xac\x81delity 算法需要 \xcb\x9c O r 21 . 5 /\xce\xb5 23 . 5 [WZC + 21]。我们的量子算法的关键思想是将块编码从先前工作中的幺正算子扩展到量子态（即密度算子）。它是通过开发几种方便的技术来操纵量子态并从中提取信息来实现的。特别是，我们基于强大的量子奇异值变换（QSVT）[GSLW19]，引入了一种用于密度算子及其（非整数）正幂的特征值变换的新技术。我们的技术相对于现有方法的优势在于，不需要对密度算子进行任何限制；与之形成鲜明对比的是，以前的方法通常需要密度算子的最小非零特征值的下限。此外，我们还提供了一些独立感兴趣的技术，用于（次规范化）密度算子的迹估计、线性组合和特征值阈值投影仪，我们相信这些技术在其他量子算法中会很有用。'](/simg/4\4e9553780581bbfda8e4d6bb48115782efffb2a7.webp)
b'我们提出了一系列量子算法，用于计算各种量子熵和距离，包括冯·诺依曼熵、量子 R\xc2\xb4enyi 熵、迹距离和 \xef\xac\x81delity。所提出的算法在低秩情况下的表现明显优于最知名的（甚至是量子的）算法，其中一些算法实现了指数级加速。特别是，对于秩为 r 的 N 维量子态，我们提出的用于计算冯·诺依曼熵、迹距离和 \xef\xac\x81delity（加性误差 \xce\xb5 内）的量子算法的时间复杂度为 \xcb\x9c O r 2 /\xce\xb5 2 、 \xcb\x9c O r 5 /\xce\xb5 6 和 \xcb\x9c O r 6 。 5 /\xce\xb5 7 . 5 1 。相比之下，已知的冯·诺依曼熵和迹距离算法需要量子时间复杂度为 \xe2\x84\xa6( N ) [AISW19,GL20,GHS21]，而最著名的 \xef\xac\x81delity 算法需要 \xcb\x9c O r 21 . 5 /\xce\xb5 23 . 5 [WZC + 21]。我们的量子算法的关键思想是将块编码从先前工作中的幺正算子扩展到量子态（即密度算子）。它是通过开发几种方便的技术来操纵量子态并从中提取信息来实现的。特别是，我们基于强大的量子奇异值变换（QSVT）[GSLW19]，引入了一种用于密度算子及其（非整数）正幂的特征值变换的新技术。我们的技术相对于现有方法的优势在于，不需要对密度算子进行任何限制；与之形成鲜明对比的是，以前的方法通常需要密度算子的最小非零特征值的下限。此外，我们还提供了一些独立感兴趣的技术，用于（次规范化）密度算子的迹估计、线性组合和特征值阈值投影仪，我们相信这些技术在其他量子算法中会很有用。'
b'我们提出了一系列量子算法，用于计算各种量子熵和距离，包括冯·诺依曼熵、量子 R\xc2\xb4enyi 熵、迹距离和 \xef\xac\x81delity。所提出的算法在低秩情况下的表现明显优于最知名的（甚至是量子的）算法，其中一些算法实现了指数级加速。特别是，对于秩为 r 的 N 维量子态，我们提出的用于计算冯·诺依曼熵、迹距离和 \xef\xac\x81delity（加性误差 \xce\xb5 内）的量子算法的时间复杂度为 \xcb\x9c O r 2 /\xce\xb5 2 、 \xcb\x9c O r 5 /\xce\xb5 6 和 \xcb\x9c O r 6 。 5 /\xce\xb5 7 . 5 1 。相比之下，已知的冯·诺依曼熵和迹距离算法需要量子时间复杂度为 \xe2\x84\xa6( N ) [AISW19,GL20,GHS21]，而最著名的 \xef\xac\x81delity 算法需要 \xcb\x9c O r 21 . 5 /\xce\xb5 23 . 5 [WZC + 21]。我们的量子算法的关键思想是将块编码从先前工作中的幺正算子扩展到量子态（即密度算子）。它是通过开发几种方便的技术来操纵量子态并从中提取信息来实现的。特别是，我们基于强大的量子奇异值变换（QSVT）[GSLW19]，引入了一种用于密度算子及其（非整数）正幂的特征值变换的新技术。我们的技术相对于现有方法的优势在于，不需要对密度算子进行任何限制；与之形成鲜明对比的是，以前的方法通常需要密度算子的最小非零特征值的下限。此外，我们还提供了一些独立感兴趣的技术，用于（次规范化）密度算子的迹估计、线性组合和特征值阈值投影仪，我们相信这些技术在其他量子算法中会很有用。'
optorbvqe.pdf
摘要：近期的量子计算机在处理信息的量子比特数量以及可连贯执行的电路深度方面将受到限制。迄今为止，出于这个原因，变分量子特征值求解器 (VQE) 等算法的实验演示仅限于使用最小基集的小分子。在这项工作中，我们建议将轨道优化方案纳入量子特征值求解器，其中将参数化的部分酉变换应用于基函数集，以减少给定问题所需的量子比特数量。通过最小化相对于该部分酉矩阵的基态能量来找到最佳变换。通过对多达 16 个自旋轨道的小分子进行数值模拟，我们证明了该方法能够大大扩展近期量子计算机在电子结构问题方面的能力。我们发现，当使用相同数量的量子比特时，与轨道优化相结合的 VQE 始终能实现比传统 VQE 更低的基态能量，甚至经常比使用更多量子比特的 VQE 方法实现更低的基态能量。
熵，压力，吉布斯通道和通用特性
m k l（v）ρl（v）†dµ（v）。T。Benoist，M。Fraas，Y。Pautrat和C. Pellegrini的最新论文是我们的起点。他们认为L是身份的情况。在量子通道φL的一些温和假设下，我们分析了φL的特征值性质，并为这种通道定义了熵。对于固定µ（先验度量）和给定的Hamiltonian H：M K→M K，我们提供了Ruelle定理的版本：与Ruelle操作员的特征值问题有关的压力变异原理（与此类H相关）。我们介绍了吉布斯频道的概念。我们还表明，对于固定的µ（支撑中有超过一个点），L的集合是φ-erg（也不可约），对于µ是一个通用集。我们描述了一个相关的过程x n，n∈N，在投射空间p（c k）上取值，并分析不变概率的存在问题。我们还考虑了一个关联的过程ρN，n∈N，d k上的值（d k是一组密度运算符）。通过Barycenter，我们将上述不变概率与x的密度算子相关联。